As promised, I would like to return to the subject of where Rick’s Chapter 7 on “Social Control” in his recent book goes off track. In particular, I want to focus on Section 7.1.7 “Conflict between Control Systems of Equal Strength.” In this section, he cites my 2004 paper, “The collective control of perceptions: constructing order from conflict.” This paper was based on the model of collective control that I had developed in the 1990s.
As I intend to show here, Rick misinterprets my model in the quotation above and, more importantly, in his description of the model in Section 7.1.7. His interpretation of my model is contradicted by mathematics of the model itself and by the plain text of what I wrote in that 2004 paper.
It seems to me that Rick fell into his long-held error about my work by jumping to a mistaken conclusion about what I must be saying when I first presented the model at a meeting of the Control System Group some thirty years ago. Without bothering to read my various papers about it carefully, he has continued ever since to hold firmly to his mistaken assumptions about my model, making erroneous claims based on his straw-man version of what I must have been saying, rather than what I actually said.
Here is the paragraph in Rick’s chapter in which he makes reference to my 2004 article, and presumably to my model, as well.
7.1.7 Conflict between Control Systems of Equal Strength
When the systems involved in a conflict are of equal strength, in terms of both gain and maximum output, the controlled variable remains in a virtual reference state (Powers, 1973b, p. 255; McClelland, 2004). For example, when arm wrestlers are of equal strength, the position of their clasped hands oscillates in a narrow band perpendicular to the table. The average position of this oscillation is the virtual reference state of the clasped hands and the position of the clasped hands is called a virtual controlled variable. Like an actual controlled variable, a virtual controlled variable is kept in a reference state protected from the effect of disturbances. If, for example, you came by and pushed the clasped hands toward one of the competitors that push would be resisted. (I would recommend not trying this yourself unless you are good friends with the competitors and tell them in advance what you plan to do.) So the clasped hands appear to be controlled because they are being kept in a reference state. But this reference state is virtual, not actual, because it is not the reference state specified by either competitor. When a variable is being kept in a virtual reference state by a conflict, none of the parties to the conflict are getting what they want; none have the variable under control. (pp. 114-115)
There’s a lot to unpack in this paragraph, but I will focus on three claims that Rick makes:
-
That my model applies only in cases in which there are multiple control systems “of equal strength, in terms of both gain and maximum output” acting on a shared controlled quantity.
-
That a “virtual reference state” and a “virtual controlled variable” appear only when the multiple conflicting control systems are operating at their maximum levels of output and that this virtual reference state represents the “average position” of the “oscillation” of the virtual controlled variable if no disturbances are present.
-
That the multiple conflicting control systems locked in such a combat are not really controlling the disputed variable collectively, because they are not “getting what they want” and thus do not have the disputed variable “under control.”
All three of these claims are mistaken. A careful examination of my 2004 paper shows that these statements are contradicted by the text, figures, and results of the model presented in the paper. Taking Rick’s claims one at a time …
Claim 1: That my model applies only in cases in which there are multiple control systems “of equal strength, in terms of both gain and maximum output” acting on a shared controlled quantity.
Granted that Rick makes this claim by implication rather than saying so directly, but this is the only place in the chapter he cites my work. In the earlier sections of the chapter, on “Cooperative Control” (7.1) and “Conflictive Control” (7.1.6), he makes no reference to my model. And his recent statement quoted above that “Kent’s model IS A MODEL OF VIRTUAL CONTROL RESULTING FROM CONFLICT” makes clear that in his mind my model does not apply in instances of cooperative control or instances of conflictive control in which “virtual control”, as he describes it, is absent.
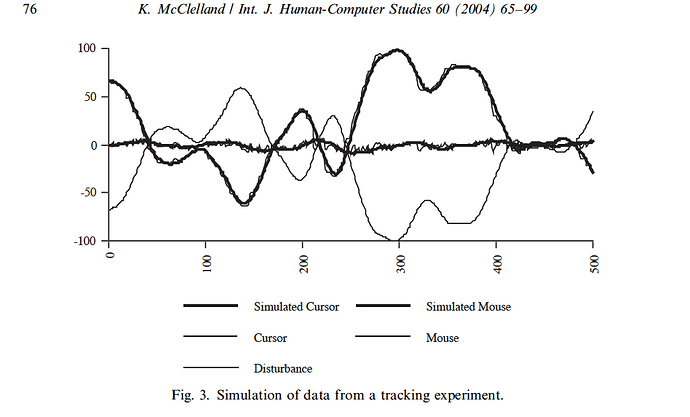
Let’s look now at what I actually said in my 2004 paper. The presentation of my model in that paper begins with Figure 3 on p. 76.
This figure showed a simulation model based on data from a standard tracking experiment, data that Rick had very kindly supplied to me. In the computations for my simulation model, I also made use of the formulas from one of the spreadsheet simulation models that Rick himself had written. So it’s not surprising that, as Rick has said, our simulation models give essentially the same results, and that our disagreement is about the interpretation of those results.
For the simulation model presented in this figure, I chose an arbitrary value of 500 as the loop gain parameter, and because the experiment, as designed, asked the subject to keep a pointer on a computer screen stabilized (in spite of disturbances) with a zero deviation from a target, I assigned 0.0 as the reference value for the simulation model, which fit the data very well. After listing the parameters of my model and describing them in some detail in the text (to allow for replication), I concluded that “the perceptual control model accurately reproduces the human actions necessary for controlling this perception” (p. 77).
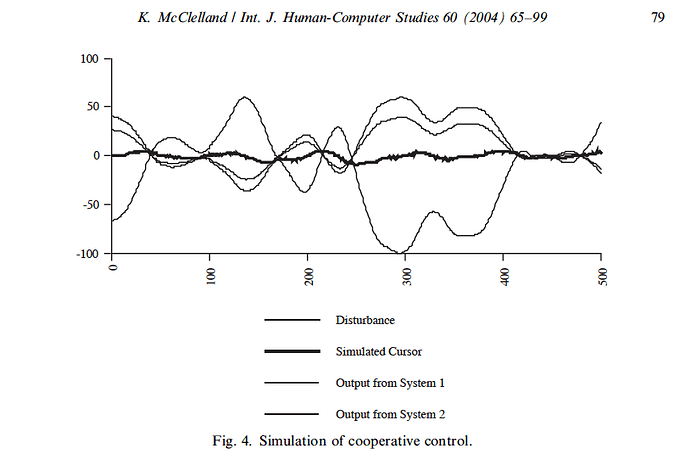
My next step in presenting my model in the 2004 paper was to offer a “Simulation of Cooperative Control” (Figure 4 on p. 79).
In this simulation, I used two control systems with different loop gains working together cooperatively to control their perceptions in opposition to the same disturbance curve used in the previous simulation. I chose a loop gain of 300 for System 1, and a loop gain of 200 for System 2 (to add to exactly 500 for the total gain, as in the previous simulation), and I assigned both control systems a reference value of 0.0. I assigned different values of loop gain to the two control agents (one half again as large as the other) so that their output curves would be distinct on the graph of the results. Because they shared the same reference value, their actions were purely cooperative.
I reported in the text that “their joint effect on that environmental variable is indistinguishable from the effect of a single control agent acting alone” and that “the simulation shows that the simulated control agents are capable of acting to control a perception jointly, and it implies that under optimum conditions their joint behavior is additive in terms of system gain” (p. 80).
Thus, the first application of my model of collective control presented in the paper was to a situation of cooperative control. I have always maintained that my model applies just as well to cooperative control as to conflictive control. The only difference between the two kinds of control in my model is the choice of the reference values for the multiple interacting agents: equal in the case of cooperative control and different in the case of conflictive control. Otherwise, the math is exactly the same. Rick’s claim that my model applies only in situations of conflict is just wrong.
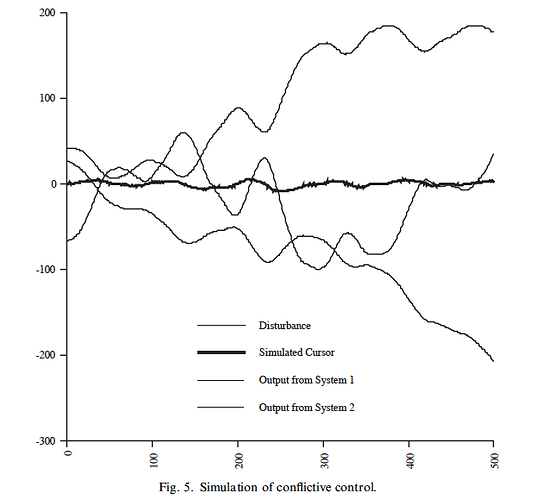
Now, let’s take a look the model of conflictive control I presented in my 2004 paper. (Figure 5 on p. 81)
In this simulation, I used the same control model as in the previous simulation of cooperative control. The only difference was that I assigned the reference value of +1.0 to System 1 and the reference value of -1.5 to System 2. Those values were not chosen arbitrarily but were chosen so that the gain-weighted sum of their reference values (300 x 1.0 = 300 for System 1 and 200 x -1.5 = -300 for System 2) would be exactly 0.0, the reference value assigned to the two agents in the simulation of cooperative control in Figure 4.
Take note, here, that in this demonstration of my collective control model, I deliberately used control systems with different loop gains in both the conflictive and the cooperative versions of the simulation. So Rick’s assertion in his quoted paragraph that my model applies only to control systems “of equal strength” is obviously incorrect.
I found, as reported in my text, that …
the pointer position curve in Fig. 5 is precisely identical to the curve for the systems sharing identical reference signals in Fig. 4, and also for the single system in Fig. 3. The two agents in Fig. 5, although engaged in conflict, have at the same time achieved joint control of the environmental variable. Despite the divergence in their outputs, the environmental variable they perceive is stabilized just as effectively by their conflictive interaction as by the actions of two similar agents with perfectly aligned reference signals or even by the actions of a single stronger system. (p. 82)
To me, at the time, this was the most significant finding to emerge from my simulations: that conflictive collective control can exert exactly the same stabilization effects on an environmental variable as cooperative collective control, and that the effects of the two kinds of collective control on an environmental variable can be identical to the effects of control by a single agent. In other words, from the perspective of an outside observer looking only at the controlled environmental variable, collective control, whether conflictive or cooperative, passes The Test for the Controlled Quantity in the same way that control by a individual controller does.
This finding was a revelation to me, because it solved a problem I had been grappling with throughout my career as a sociologist. Late twentieth-century sociology was dominated by three competing schools of thought about how society works:
“Functionalist” theory held that societies have evolved different ways of performing the functions necessary for a society to survive, like providing economic and political structures for supporting a way of life and keeping order, family and educational structures for reproducing the next generation and socializing children into the norms and values of the society, social control structures for punishing and eliminating deviance, etc. These structures do not entirely eliminate social change, but because of the fact that individual members of society internalize the society’s values, norms, and customary ways of doing things, change ordinarily tends to occur slowly. This view of society emphasized cooperation between people and continuity over time.
“Conflict” theory, functionalism’s main competitor, focused on the forces driving societies apart and sometimes leading to revolutionary change. Conflict theorists argued that economic inequality creates deep social divisions, primarily conflict between social classes, but also race and gender conflict, and that social change results from the struggles between powerful groups and the groups they oppress. According to this view, powerful groups capture the apparatus of the state, the media, and religion in order to lock in their advantages and impose their preferred social order, but conflict is always endemic in society, as less powerful groups continually resist their oppression.
A third school of thought, called “symbolic interactionism,” looked at society from a social psychological perspective. Researchers in this tradition studied small groups and the interactions between individuals. They focused on individual agency and argued that individuals draw pragmatically on the larger patterns of society to organize and structure their own interactions with others and to construct and defend their sense of self. Group structures, then, emerge from the repeated interactions of individuals, who often improvise as they go along, seeking to fulfill their own goals, maintain their own social identity, and establish order in their own surroundings.
I had absorbed these theories of society during my own schooling and had taught them to my introductory sociology and social theory students for years, always asking them to examine critically the empirical evidence sociologists had offered in support of these various points of view. When my simulations showed, then, that perceptual control theory offered a unified model capable of explaining both social stability and social conflict, and moreover, a model based on the autonomy and intentionality of the individual, I began to see PCT as a way of bringing theoretical coherence to the discipline of sociology, a discipline that had never yet settled on a coherent story of how societies work. I still hold that vision of what PCT can do for sociology.
Turning next to Rick’s second claim …
Claim 2: That a “virtual reference state” and a “virtual controlled variable” appear only when the multiple conflicting control systems are operating at their maximum levels of output and that this virtual reference state represents the “average position” of the “oscillation” of the virtual controlled variable if no disturbances are present
Although I didn’t use the terminology at the time, and in retrospect it was probably a mistake, the simulation results I presented in my 2004 paper also demonstrated that collective control, whether cooperative or conflictive, always produces a virtual controller and virtual reference value, whether or not the control agents are operating at maximum output.
The second and third versions of the simulations, the cooperative and conflictive collective control simulations (Figures 4 and 5), demonstrated that control agents working collectively could control an environmental variable as if they were a single agent with a loop gain equal to the sum of their loop gains (500 in these simulations) and a reference value equal to the gain-weighted average of their reference values (0.0 in all three simulations).
In other words, Figure 3, the simulation of control by a single agent, represented the virtual controller generated by the collective control by the two agents in both simulations of collective control (Figures 4 and 5). And the zero line on the graphs represented the virtual reference value for both kinds of collective control. Notice that the none of the agents in these simulations was operating anywhere near its maximum output level, but a virtual controller emerged all the same.
In fairness to Rick, he’s now fully aware that a “virtual reference state” emerges anytime that two or more controllers are attempting to control their perceptions of the same environmental variable using different references (i.e., in conflictive collective control). As he noted in a recent response to one of my earlier posts.
Unfortunately, he seems to have overlooked this fact when he asserted in the paragraph quoted above that …
a “virtual reference state” and a “virtual controlled variable” appear only when the multiple conflicting control systems are operating at their maximum levels of output.
Rick’s apparent confusion on this point probably derives from Bill’s description of a “virtual reference level” that can emerge in a stalemated conflict in his chapter on “Conflict and Control” in Behavior: the Control of Perception, which was the other source cited there along with my 2004 paper. Here’s what Bill wrote:
Conflict is an encounter between two control systems, an encounter of a specific kind. In effect, the two control systems attempt to control the same quantity, but with respect to different reference levels. For one system to correct its error, the other system must experience error. There is no way for both systems to experience zero error at the same time. Therefore the outputs of the systems must act on the shared controlled quality in opposite directions.
If both systems are reasonably sensitive to error, and the two reference levels are far apart, there will be a range of values of the controlled quantity (between the reference levels) throughout which each system will contain an error signal so large that the output of each system will be solidly at its maximum. These two outputs, if about equal, will cancel, leaving essentially no net output to affect the controlled quality. Certainly the net output cannot change as the “controlled” quantity changes in this region between the reference levels, since both outputs remain at maximum.
This means there is a range of values over which the controlled quantity cannot be protected against disturbance any more. Any moderate disturbance will change the controlled quantity, and this will change the perceptual signals in the two control systems. As long as neither reference level is closely approached, there will be no reaction to these changes on the part of the conflicted systems.
When a disturbance forces the controlled quantity close enough to either reference level, however, there will be a reaction. The control system experiencing lessened error will relax, unbalancing the net output in the direction of the other reference level. As a result, the conflicted pair of systems will act like a single system having a virtual reference level between the two actual ones. A large dead zone will exist around the “virtual reference level,” within which there is little or no control. (pp. 266-267 in the 2005 edition)
Unfortunately, it seems to me this is a case in which Bill’s intuitive observations of everyday experiences, which were usually so incisive, had played him false. He had never, as far as I know, tried to model this kind of conflictive interaction to check the validity of his intuitions about it. (Rick didn’t present any models in his Chapter 7, either, to back up his assertions about the way social interactions work, except for his model of the divergence in the pronunciation of diphthongs by subpopulations on Martha’s Vinyard. And even in the case of that model, Rick didn’t provide enough technical detail for another investigator to replicate his findings.)
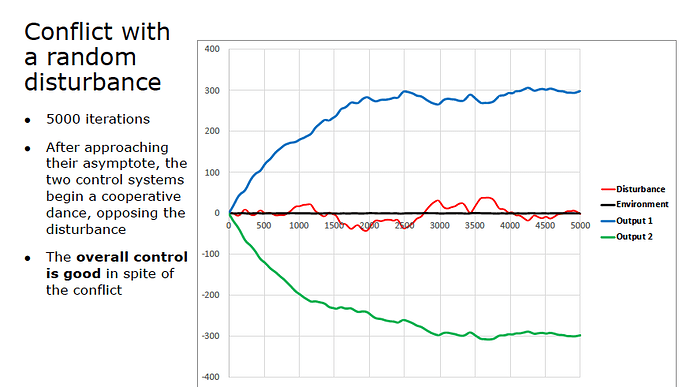
My 2004 paper reported a simulation that I did to test Bill’s prediction about emergence of a “dead zone” in episodes of conflictive control in which both control systems have reached their maximum output. Here is the graph of my simulation:
My computer resources at the time were too limited for me to investigate simulations long enough for the control agents in conflict to reach some “naturally occurring” maximum output, so I imposed a hard limit of 100 points either way on the output of both control systems. To speed up the conflict, I gave the two control systems reference values that were 10 times as far apart as in the previous simulations, +10 for the system with a loop gain of 300 and -15 for the system with a gain of 200. My choice of reference values meant that the virtual reference value for their combined action was again the zero line, the gain-weighted sum of their reference values. Here’s how I described the results:
The wider gap between reference values leads to a much more rapid escalation of the conflict, and both agents soon hit their output limits, exerting 100 points of pull in either direction. When the conflict becomes deadlocked in this way, an interesting effect occurs. As long as the two outputs are equally balanced against each other, the only force leading to any change in the environmental variable is the disturbance, and the environmental variable begins dutifully following the disturbance, until the disturbance pulls the variable outside of the disputed region between the reference lines. Whenever the variable reenters the disputed region, the system whose reference line has been crossed can relax enough to move away from its output limit and thus begin again to control. So, the variable stays near the reference line for the system in control. The control lasts, however, only until the disturbance begins pulling the variable back toward the other system’s reference line, at which point the first system once again runs into its output limit and loses control. (pp. 82-83)
What did not happen in this simulation is what Bill had predicted: that there would be little or no control within the dead zone. Instead, for the most part, the two control agents alternately traded control whenever the disturbance pulled the environmental variable close enough to the reference value of one of the agents’ reference lines to allow it to relax its output away from its hard maximum, thus giving it the freedom of action to keep the environmental variable near its own reference, while the other agent was incapacitated because its output was at its maximum. Sometimes, when both agents had hit their maximum output, control was in effect ceded to the disturbance, and the environmental variable tracked the disturbance line. Since neither agent was free to act in those segments of the simulation, they had indeed lost control. Otherwise, the control was just traded back and forth between the agents, not lost entirely.
Another thing that did not happen in this simulation, except for the brief moments when neither control system had hit its hard maximum, was Bill’s second prediction, that the two systems would act “like a single system having a virtual reference level between the two actual ones.” The only time that the environmental variable stayed near the reference level for the virtual controller, which again in this simulation was the zero line (not actually shown on the graph), was in the first few iterations, before either system had run into the maximums I had imposed on their output. In sum, although I didn’t notice it myself at the time, neither of Bill’s predictions about the “dead zone” had been confirmed by this simulation.
There was, in fact, no need for me to impose hard limits on the control agents’ output. Natural limits on output exist in every episode of conflictive control, because the total loop gain of the interacting agents is limited. As I showed in my presentation for the IAPCT conference last October (https://www.researchgate.net/publication/367240652_A_Fresh_Look_at_Collective_Control_and_Conflict), in conflictive control the outputs of the conflicting agents diverge rapidly until both approach asymptotes imposed by their limits on loop gain, at which point they begin to work cooperatively to keep the environmental variable near the reference value of their virtual controller. Here is a graph I showed in my presentation last fal (slide 13):
In this graph, the red line is the disturbance. The black line is the trace of the path of the environmental variable, which looks virtually straight, because the reference values for the two conflicting systems are close together (1.0 for a system with gain 300 and -1.5 for a system with gain 200, as in the Figures 4 and 5 above) and the control is excellent. These two very high-gain control systems are working together to make the environmental variable track the zero line (the virtual reference level) almost precisely, with deviations too small to show up on a graph of this scale.
Clearly, collective control is just another form of control, even when the participating control agents are locked in conflict with each other, and the conflict has driven them to their maximum levels of output. In terms of the environmental outcome of their interaction, the control that conflicting agents can exert by working together is indistinguishable from the cooperative control they could accomplish if they agreed on a reference value for the variable they jointly perceive, and also indistinguishable from the control that could be exerted by a single (virtual) control agent that had a loop gain equal to the sum of their gains and a (virtual) reference value equal to the gain-weighted mean of their reference values.
Which brings us to Rick’s third claim in his paragraph from Chapter 7:
Claim 3: That the multiple conflicting control systems locked in such a combat are not really controlling the disputed variable collectively, because they are not “getting what they want” and thus do not have the disputed variable “under control.”
This claim is simply nonsense. As I’ve shown above, even when control is conflictive, collective control is always just control unless environmental barriers, like the hard limits imposed on their output in Figure 6, restrict the freedom of action of the agents involved.
Besides, in the PCT model control is never perfect, with the control agent getting exactly what it wants. There always remains a residual gap between the agent’s perception and its reference value even with the tightest control, and it’s that gap (the error = r - p) that drives the control system’s output. The size of the gap, of course, depends on the loop gain, but cranking up the gain to tighten the control will only produce instability in the system’s output. To insist that control is not control unless it’s good control makes no sense. Where do you draw the line between good and bad control?
It appears that Rick fell into his confusion on these points by accepting Bill’s misleading description of deadlocked conflict in B:CP as gospel, without ever taking the time and trouble to read my papers carefully, think through what I was saying, and consider whether I might actually be right.
To act the part of a real scientist harboring doubts about my published work might have cost him some additional time and trouble. He might have had to run his own simulations to check my results and then do a series of experiments with live subjects to confirm or disconfirm the predictions derived from my simulations. In any case, he didn’t bother.
Instead, Rick has wasted countless hours of his own and other people’s time over the last three decades by defending his distorted version of my work in his online arguments with me and with several other people who have carefully read my papers and understand what my theory says. What a waste of time and effort! What a pity!
To readers who have found this detailed recitation of results from a paper now almost twenty years old a little tedious, I understand, and I apologize. But I felt I needed to go on record by laying out explicitly what has been wrong with Rick’s description of my work. I would be very happy if I have now managed to clear up his confusion on these points and in so doing have finally laid this long-simmering controversy to rest, but I’m not too hopeful about that outcome, given Rick’s impulse to double down on his own position anytime anyone calls one of his pronouncements into question. Wouldn’t it be great if we elder statesmen could start listening to and learning from each other and get back to extending and clarifying PCT for people newly interested in it, instead of spinning our wheels in these silly arguments?
My best,
Kent