Rick,
Take a look at:
David
···
----- Original Message ----- From: "Richard Marken" <rsmarken@GMAIL.COM>
To: <CSGNET@LISTSERV.UIUC.EDU>
Sent: Friday, April 11, 2008 12:35 PM
Subject: Re: Perception and PCT
[From Rick Marken (2008.04.11.0940)]
Bill Powers (2008.04.11.0759 MDT)
>Rick Marken (2008.04.10.2310) --
> It seems like whatever I find it makes Martin's point.
I wish you would stop making snide remarks about Martin.
I don't see what's snide about that remark. But I'll wish for me to
stop making then, too. Though I think it's part of my charm.> "The perceptual signal is perfectly correlated with qi when the noise
> amplitude is zero. The quality of control, measured by S, is nearly
> perfect (S = ~1.0). When noise is added the correlation between p and
> qi goes down in proportion to the amplitude of the noise. However,
> adding noise that brings the correlation between p and qi down to
> nearly zero hardly affects the quality of control at all (S ~ .98).I find that very hard to understand. Without the noise, p = r and is
constant. So control looks perfect. But when you add internal high-frequency
noise to p without directly affecting qi, p begins to vary right along with
the (internal) disturbance... Control of qi relative to the same internal
disturbance would be far better... I guess I don't understand how you set
up the situationI think you understand the set up. What was unclear, I think, was what
I meant by control of p and qi. When the high frequency (broad band)
noise was added to p, the variance of p was, indeed, greater than the
variance of qi (which is 0.0). However, control of p, was measured asS = 1 - sqrt(var(p)/[var(d)+var(o)])
where d is the narrow band disturbance to qi and o is the output
effect on qi. The value of S is nearly perfect (1.0 is perfect and I
get S values of .98 or more) when low amplitude broad band noise is
added to p, even though the correlation between qi and p goes down to
near 0.0.Of course, the value of S for qi -- S = 1 -
sqrt(var(qi)/[var(d)+var(o)]) -- is higher than for p (1.0 compared to
~.98) but the point of the demo (from my perspective) was to show that
control (measured in terms of stability of qi or p) can be quite good
even when there is no correlation between qi and p. It seems to me
that this demo proves that accurate information about qi (which would
be a high correlation between qi and p) is not needed for control."Information" is a technical term in Martin's argument, and the only way to
draw conclusions is to calculate the information content according to the
definitions. We should wait for Martin to do that.I was going to suggest, in my original description of the simulation,
that Martin calculate the information transmitted about qi when the
correlation between qi and p is 0. I can't remember the exact formula
for transmitted information (which Shannon called H) but I think it
was something like:H = Sum [log2 (Pr(p|qi))]
That is, information is, technically, a log (base 2) function of the
conditional probability of getting particular values of p given
particular values of qi summed over the range of possible qi (the
messages). I can't see how H can come out to be anything other than 0
when the correlation between qi and p is 0. But I agree that we should
wait for Martin to do that. In the meantime I'll try to find the
information transmission measure myself and see how much information
is actually transmitted in this simulation. If anyone out there
happens to know off hand Shannon's formula for H please let me know
and I'll compute it in my simulation.Best regards
Rick
--
Richard S. Marken PhD
rsmarken@gmail.com
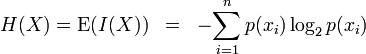 So I was off by a minus sign and a multiplication.
So I was off by a minus sign and a multiplication.