[Bruce Nevin (2016.01.20.12:42 ET)]
Martin Taylor Nov 29, 2015 at 9:04 AM –
I never responded to this. My apology. It got lost in the post-Thanksgiving shuffle. You posed a multiple-choice quiz. My answers are interleaved.
I will ask you three questions. The first is about your use of language, the second is contingent on your answer to the first, and the third on your answer to the second.
- Under which of the following conditions, if any, do you consider a variable to be controlled:
(a) when disturbed from an apparent resting position it returns to or near that position.
Your (a) is a necessary but not sufficient condition.
The variable need not be resting as a precondition for observing resistance to disturbances, and it’s usual to talk of the value of a variable rather than its position–presumably a position on some scale of values.
(b) when disturbed from an apparent resting position, it returns to or near that position as the result of an observable effect from a source other than the observed disturbing influence.
The observer perceives the source of q.o as being distinct from the source of d. I don’t know why you’re being coy about identifying the “source other than the observed disturbing influence” as the subject’s behavioral outputs q.o. This is necessary for applying other criteria that are essential to the Test (q.v. below).
A caveat: In an internal conflict, the source of the disturbance is within the observed organism so that we have two loops within the hierarchy, each with its q.o which can eventuate in two successive values of q.o observed in the common environment. (The q.o of one provides a reference for effectors and then the q.o of the other provides a different reference for the same effectors.)
Again, your (b) is necessary but not sufficient.
(c) when disturbed from a resting position apparently determined by some other variable, it returns to or near that resting position as the result of an observable effect from a source other than the observed disturbing influence.
I do not understand what distinction you intend to make here.
The only significant difference between (b) and (c) is the phrase “apparently determined by some other variable”. Here’s a breakdown to show the parallels. (I’ve put two irrelevantly discrepant words in italics.)
(b) when disturbed from an apparent resting position,
(c) when disturbed from a resting position
(c) apparently determined by some other variable,
(b) it returns to or near that position
as the result of an observable effect
from a source other than the observed disturbing influence.
(c) it returns to or near that resting position
as the result of an observable effect
from a source other than the observed disturbing influence.
The most salient reading is that the “[apparent] resting position” of the variable appears to the observer to be “determined by some other variable”. On either reading, I don’t understand what you’re driving at.
First, other than what? Assuming you mean other than the disturbance, are you saying that some (unnamed) variable other than the disturbance has determined the (resting) position? Or is the other variable q.o but for some reason (as above under (b), perhaps) you’re not yet warranted to call it that? Surely, we presuppose that we are observing the subject organism’s activity?
Another possible reading is that it is the disturbance that “appears to be determined by some other variable”.
On that reading, it is even less clear “other than what”. Are you saying that some (unnamed) variable other than q.o has determined the (resting) position of the variable? Or (again) is q.o the “other variable”?
OK, assuming that reading, I’ll venture a paraphrase:
(c) when disturbed from a resting position that was apparently determined by
the subject’s prior actions (which we can’t yet call q.o for some reason),
it returns to or near that resting position as the result of an observable effect from
the subject’s present actions (which we can’t yet call q.o for some reason).
But no, some other agent might well have arranged the variable in a state that is no disturbance for the subject. So I can’t see the relevance of the distinction in (c). Surely no one would dispute that the socalled ‘resting position’ was determined by some prior cause or causes.
There are other necessary conditions in addition to (a) and (b), including:
(d) The subject organism must be able to perceive the putatively controlled variable.
(e) The subject must actually be perceiving the variable when observations of putative control are made.
(f) The subject’s activity must be able to affect the state of the variable.
(g) Actual subject outputs q.o must be observed to cancel the effects of d on the variable.
(h) Observer can and does predict the effect of d if q.o is not present.
(i) The disturbance d avoids side effects disturbing other variables that the subject might be controlling.
There may be more that I’m overlooking in a quick look through Phil Runkel’s summary statement in People as living things (2003:77-79), which in turn was based on Powers (1973:232-246; 2005:233-248; 1979:110, 112), and (I am sure) conversations with Bill, including the correspondence reprinted in Powers & Runkel (2011).
- If your answer includes (a) or (b), do you think it possible to have two independent controlled variables in a standard PCT control loop?
The framing of the question suggests to me that you see these choices as mutually exclusive. I do not say that (a) or (b) is sufficient. I do say that (b), which subsumes (a), is necessary as are also (d)-(i). I don’t understand (c)
But what is most striking to me about your question (2) is the word “independent”.
The question is not about independent controlled variables. p is certainly dependent upon q.i, and the chain of dependency goes all the way around the loop, q.i dependent on q.o + d, q.o dependent upon r - p. Perhaps the assertion that q.i and p are both controlled is a disturbance to you because you understand this to mean that they are independently controlled. They are two aspects of one thing. q.i is the controlled variable CV as perceived by an observer, and p is the same CV as perceived by the subject.
And that is my answer to your third question.
···
On Sun, Nov 29, 2015 at 9:04 AM, Martin Taylor mmt-csg@mmtaylor.net wrote:
Bruce,
I will ask you three questions. The first is about your use oflanguage, the second is contingent on your answer to the first, and
the third on your answer to the second.1. Under which of the following conditions, if any, do you considera variable to be controlled:
(a) when disturbed from an apparent resting position it returns toor near that position.
(b) when disturbed from an apparent resting position, it returns toor near that position as the result of an observable effect from a
source other than the observed disturbing influence.(c) when disturbed from a resting position apparently determined bysome other variable, it returns to or near that resting position as
the result of an observable effect from a source other than the
observed disturbing influence.2. If your answer includes (a) or (b), do you think it possible tohave two independent controlled variables in a standard PCT control
loop?3. If your answer to (2) is no, which variable in the standard PCTcontrol loop is controlled?
--------- My answers: 1-only c, 2- No, 3-the perception. (I answered 2 as atautology, given that 1c precludes a yes answer to 2).
Martin On 2015/11/28 10:54 PM, Bruce Nevinwrote:
[Bruce Nevin (2015.11.28.22:53 ET)]
Martin Taylor (2015.11.26.14.54)–
BN: This was in responseto a person who denies that Qi is controlled at all.
MMT: I have read Borisas simply pointing out that the output affects Qi in
order that perception is controlled. I say the same.
BN: if that were thecase, there would be no way for an observer to notice
the fact of control. No stabilization of the
environment against disturbances would be perceptible
to anyone except the organism that was doing the
controlling.
MMT: Why not? I never perceived you as being of theall-or-none Black or White persuasion, but here you
are saying that if (as must be the case) an observer
has a different set of inputs to the senses than the
person doing the controlling, no matter how similar
their inputs and perceptual functions may be, what the
observer sees must be totally unrelated to what the
controller sees. Sure, if the controller is
controlling the placement of a glass on a table, and
the observer is looking at the degree to which a door
is open, the observer will say there’s no control. But
that’s not what we are talking about, is it? The
observer sees the glass on the table, and if he wants
to know whether the controller cared where it was
placed, the observer can become an experimenter and
move it. The fact that they see it from different
angles may matter, but probably doesn’t.
I am not at all saying that since inputs to theobserver’s senses are different from the inputs to the
senses of the subject, “what the observer sees must be
totally unrelated to what the controller sees”. Although as
I attempt in vain to relate that to what I said, it does
seem that you may be exemplifying what you said.
I am saying that in your glass scenario or in the TCV theperception that each of the participants controls is related
to the perception that the other controls by way of
that aspect of their common environment which they are controlling .
To talk about that relationship of the observer’s perception
to the subject’s perception, you prefer to say that the
perception that each of them controls is related to the
perception that the other controls by way of that aspect of
their common environment which they are influencing .
I assume you have a purpose for that choice of words, but
you have not stated it. I have a purpose in saying that * Qi*is controlled. I will explain that here.
In the TCV, the tester controls variables until a(gentle) conflict with the subject is confirmed. That
conflict affirms that they are both controlling the same
aspect of the environment. Or in your words, they are both
influencing the same aspect of the environment. That
controlled or influenced aspect of the environment is
quantified as Qi. The controlled perception p is a
transform of Qi from physical units measured in the
environment to (per the PCT model) a rate of firing in a
nerve or nerve bundle. The transformation by the input
function is quantified as a constant Ki . You have
objected that imperfections in the sensory apparatus make Ki a
noisy variable. My rejoinder was that if that has any
significant effect at all, and is not zeroed out as just
another disturbance in the loop, the effect is that Qi is
less well controlled than p is, but Qi is
nonetheless still controlled.
As far as I can see, to say that the tester and thesubject are merely influencing Qi (or that aspect of
the environment which is quantified as Qi ) as means
of controlling their respective perceptions is sophistry, a
terminological distinction without a difference, serving no
purpose and confusing the issue. Or if you do have a purpose
in making that distinction, please do say what it is. But
even my astigmatism does not interfere with my ability to
put that glass back where I want it, so perfect me no run of
the mill sensory imperfections, please. Or, more politely,
let us say that I remain unconvinced.
Perceptual control has environmental consequences thatare perceived (and can be controlled) by others. Your
position is that when a perception is controlled the
environmental consequences are not controlled. In my view,
environmental consequences that are not controlled are
called side effects.
In your view, the environment is merely influenced bycontrol activities in order that the perception may be
controlled. The perceived influence is controlled, but the
influence that is perceived is not controlled. The intended
environmental consequences of that influence do not
constitute control of the affected aspect of the
environment. I say that there is evidence that the affected
aspect of the environment is controlled, and that the
environmental consequences of control, as perceived by
others, measured by instruments, etc., are controlled. The
effect is intentional. Indeed, the nature of that effect is
precisely, control. One kind of evidence is that it is
perceived by another as control. “What are you doing to that
glass?” Another is that the tester’s perception (from the
imagined point of view of the subject) is sufficient basis
from which successfully to deduce the subject’s internally
maintained reference value for p . Another is that
conflict often has environmental consequences (“Now see what
you’ve done! You’ve spilled the water!”) which may disturb
collectively controlled variables. Collective control is yet
another kind of evidence: stabilization of what? An * environmental*feedback path.
Perhaps you are brought to your position in part by thetestimony of the physical sciences that the objects,
relations, and events that we perceive devolve to shifting
arrangements of subatomic particles and energy.
Did old Sam Johnson bruise his foot in vain?
The assumption that perceptions are veridical, and thatcontrol of a perception indicates control of that which is
perceived, is the converse of a sacrament. A sacrament, as
you may recall, is said to be an outward and visible sign
of an inward and spiritual reality. A controlled
perception is an inward and perceptible sign of an outward
reality which, aside from perceptions, is unknowable. The
latter is as much an article of faith as the former. Yet
it certainly seems not so, because of our existential
reliance on perceptions. Indeed, faith of the sacramental
sort is characterized by belief without evidence; and your
claim seems to amount to saying that the only evidence we
have, our perceptions, is no evidence at all. As Alice
would say, curiouser and curiouser.
I have two questions:
- How do you avoid solipsism?
What explanatory principles do you invoke to accountfor how the Test for the controlled variable discloses
the subject’s CV on the basis of your perceptions?
(Let the TCV serve as first proxy for the other kinds
of evidence enumerated above.)
I postulate only one explanatory principle: that anaspect of the environment is controlled when a perception
is controlled.
We derive our conviction as to the veridicality ofperception from the mutual consistency of many
perceptions, including our incessant informal testing of
what variables those around us are controlling.
Collaboration, collective control, conflict and its
resolution, all hinge upon a public actuality that is
commonly affected by the separate and private control of
perceptions by the participants, thereby confirming again
and again that control of perceptions is by means of
control of the perceived environment. Is that confidence
ill founded?
The physical universe, whatever it is, is resistant toour control activities. When you shift the alignment of a
dime in the coin game or a glass on the table it stays put
when you take your hand away. Presumably, that resistance
emerges from what seems to be an infinite plasticity of
subatomic phenomena somehow–collective control by
infinitesimal points of energy/consciousness?–but however
it comes about, a consequence is that control through the
environment is very different from control in imagination.
When we control our perceptions, we do so by overcoming
the inertial character of material things, by making
changes in the environment which are perceived as effects
of our control of perceptions. And a great many of those
effects endure in our absence until our return. The
furniture is where we left it. Ah, that’s where I left my
glasses, now I remember.
I know he's a crotchety old fellow, but let Mr. Ockhamhave a word. On offer is a single explanatory principle to
account for all this: an aspect of reality is controlled
when the perception of it is controlled. Please show us
how any other account avoids multiplying explanatory
principles.
/Bruce
On Thu, Nov 26, 2015 at 3:21 PM,
Martin Taylor mmt-csg@mmtaylor.net
wrote:
[Martin Taylor2015.11.26.14.54]
[Bruce Nevin (2015.11.25.20:04 ET)]
Martin Taylor 2015.11.24.23.37 –
when [disturbances] appear between thecontrolled variable p and the complex
environmental variable (the CEV) to which it
corresponds, all that means is that the CEV is
not controlled as precisely as the perception
is
Yes, but it is controlled, howeverimperfectly that may be.
I deny that. The appearance of control of teh Complex EnvironmentalVariable is, if I understood you correctly when you used
the term in another context, a spandrel. The appearance
that is is controlled is a consequence of something else
truly being controlled. It used to be quite obvious that
phlogiston flowed in and out of objects, and even now we
observe heat flowing in and out of objects, but there’s
“really” no flow of anything. All there is is a bunch of
molecules moving around and beating the hell out of each
other. It’s the same kind of thing. When we talk
casually, I have no objection to saying that the CEV is
controlled. I do it myself quite often. But when we want
to explain the theory to anyone in or out of CSGnet, one
of the very first things we have to explain is that the
CEV is not controlled, however much it looks as though
it is. The perception of it is controlled, and that is
the reason it looks as though it is controlled (as also
is everyone else’s perception of anything correlated
with the CEV, though that fact is never mentioned in
this discussion; why should the argument not be that the
controller is controlling what some undefined other
person is perceiving? The logic is the same.).
You're denying my assertion that adisturbance at that point in the loop can be
resisted.
No I most definitely am not!!! If it were notresisted, how could the corresponding perception be
controlled?In the case of a pathology, it is certainlythe case that control is impaired, as I said.
Example: before the invention of corrective
lenses, my astigmatism would require me to rely
on others to make out details of a scene and
report them, as would my relatively slight
myopia.
Look, all I'm trying to do is to emphasizethat PCT is about The Control of Perception,
something that seems in danger of being
forgotten even on CSGnet.
Yes, but consider the context. This was inresponse to a person who denies that Qi is
controlled at all.
I guess we bring different prior assumptions toour reading of what always must be ambiguous, and that’s
foubly true of someone whose first language is no
variety of English. I often disagree with what Boris
says, but on this I have read Boris as simply pointing
out that the output affects Qi in order that
perception is controlled. I say the same, but I am not
usually told I don’t understand PCT – at least not in
the 20 or so years since Bill challenged Rick when he
made that claim, saying something along the lines of
“Who do you think you are saying doesn’t understand
PCT?”I agree with Rick: if that were the case,there would be no way for an observer to notice
the fact of control. No stabilization of the
environment against disturbances would be
perceptible to anyone except the organism that
was doing the controlling.
Why not? I never perceived you as being of the
all-or-none Black or White persuasion, but here you are
saying that if (as must be the case) an observer has a
different set of inputs to the senses than the person
doing the controlling, no matter how similar their
inputs and perceptual functions may be, what the
observer sees must be totally unrelated to what the
controller sees. Sure, if the controller is controlling
the placement of a glass on a table, and the observer is
looking at the degree to which a door is open, the
observer will say there’s no control. But that’s not
what we are talking about, is it? The observer sees the
glass on the table, and if he wants to know whether the
controller cared where it was placed, the observer can
become an experimenter and move it. The fact that they
see it from different angles may matter, but probably
doesn’t.Martin
/Bruce
On Tue, Nov 24, 2015 at
11:59 PM, Martin Taylor mmt-csg@mmtaylor.net
wrote:
[Martin Taylor 2015.11.24.23.37]
On 2015/11/24 10:37 PM, Bruce Nevinwrote:
[Bruce Nevin (2015.11.24.ET)]
MartinTaylor (2015.11.24.14.02) –
"PCT"doesn’t imply it. It’s simply
a fact of life (and of
engineering) that ONLY if the
connection from Qi to the
perceptual variable is
invertible, perfect, and
noise-free will there be no
difference between the ECV
(whatever that may be) and the
perception. The perception is
controlled, and as a
consequence, the environmental
variable appears to be. As an
approximation, it’s good
enough for most purposes, but
like Newtonian gravity, it’s
not a good foundation for
theoretical discussion or
precise analysis.
Inthe equations that I’m familiar
with the connection from * Qi*to p is
represented by a constant Ki .
So it is, but how realistic do you thinkthat is in the real world of live
organisms?Hasn'tthat sufficed for implementing
simulations, or have I missed
something?
As I said: " As anapproximation, it’s good enough for most
purposes,". Does anyone claim that the
simulations actually represent what goes
on inside the organism? Even the concept
of a neural current has no equivalent in
an actual brain. It’s an analytical
convenience, an abstraction that simply
assumes that the effect of a lot of
neurons firing with their own timings is
the same as though one super-neuron
performed all the firings, and then
smeared them across time so that a
smooth variation was used in further
functions. For most purposes, that’s
fine, but if you really want to think
about it, Bill just said that if it’s
within a few percent (5%, 2%, I forget)
that’s good enough. And it usually is.
But it doesn’t mean that it’s perfect.Any imperfection and noise inthe biological implementation is
just another disturbance.
Disturbances can enter at any
point in the loop.
Indeed, but when they appearbetween the controlled variable p and the
complex environmental variable (the CEV)
to which it corresponds, all that means is
that the CEV is not controlled as
precisely as the perception is.If such disturbances could notbe countered by the control
process in the same way that
environmental disturbances are,
and if they were great enough to
make p depart from its
correspondence to the relevant
aspect of the environment, as
represented by Qi , they
would be pathologies making it
less likely for that organism to
succeed in bringing offspring to
reproductive maturity, so there
is obvious evolutionary pressure
for that coupling to be quite
good enough to support good
control.
Yes. That, in essence, is what Isaid when I said “it’s good enough for
most purposes”. You have read a lot of my
writings. How often have I written in
things addressed to PCT newbies that
though what is controlled is perception,
it’s what happens in the environment that
matters?That seems to me a pretty strongbasis for that coupling being
treated as a constant Ki .
rather than as a variable
subject to significant
unpredictable perturbations.
Much more likely to be some kindof approximation to log(Qi) with some kind
of ceiling and some kind of zero-region
tolerance zone.It doesn't matter, what the function is,if it’s invertible. noise free, and
consistent (which adapting systems are
not).Look, all I'm trying to do is to emphasizethat PCT is about The Control of
Perception, something that seems in
danger of being forgotten even on CSGnet.Martin/Bruce
On Tue, Nov
24, 2015 at 2:44 PM, Martin Taylor
mmt-csg@mmtaylor.net
wrote:
[Martin Taylor2015.11.24.14.02]
[From RickMarken
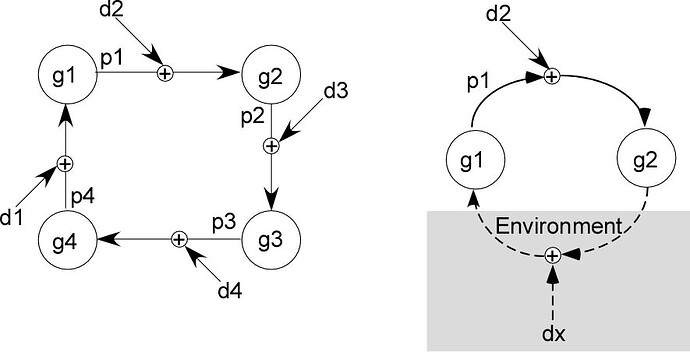
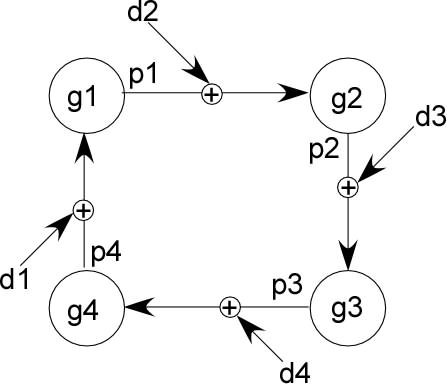
(2015.11.22.0950)]
No. p1 is thecontrolled quantity, the
perception that tracks the
reference value -d2 closely if
all the g values are
substantially greater than
unity. In a real control loop,
of course, the “g” multipliers
would represent the long-term
stable values of the leaky
integrators, just as in the
usual analysis of the simple
control loop. The actual loop
could not use simple
multipliers. When there are
loop delays, simple
multipliers inevitably lead to
oscillation and no control. My
analysis was of the stable
equilibrium values, and for
that, the leaky integrators
are well represented by simple
multipliers.And what's an "ECV"?
Yes, I am interested.It’s good to have the
spreadsheet example. What gain
and leak rates did you use for
the four “g” functions, to get
the “g” multipliers? The
effect of d4 and d3 is
diminished by the multiplier
ratio each step back round the
loop. My analysis assumed,
g>>1, as we do when we
do an equilibrium analysis of
the ordinary control loop and
assume the loop gain
G>>1.I imagine that in yourspreadsheet you have a scalar
variable and a simple
multiplier, as I showed in the
example. One can’t actually
run the TCV on a single
scalar, because there is no
function to be found. But it
would be interesting to run a
spreadsheet example in which
each of the paths was a vector
of, say, three scalars, and
each perceptual function was
different, and then run the
TCV to see what you find.
"PCT" doesn't imply it. It'ssimply a fact of life (and of
engineering) that ONLY if the
connection from Qi to the
perceptual variable is
invertible, perfect, and
noise-free will there be no
difference between the ECV
(whatever that may be) and the
perception. The perception is
controlled, and as a
consequence, the environmental
variable appears to be. As an
approximation, it’s good
enough for most purposes, but
like Newtonian gravity, it’s
not a good foundation for
theoretical discussion or
precise analysis.
That's at leastequally wrong. I think it
might be worth your while to
look a little more closely
into the actual conditions for
using the TCV, and the
potential and limitations on
what you can determine by
using it. You often seem to
suggest (planning in
imagination) that you might
use the TCV in real-life
situations. Sometimes the
conditions are suitable, but
much more often, they aren’t.
I haven’t done it, so I am
also planning in imagination,
but one ought to be able to
run the TCV on your demo of a
three-level control system to
find what is being controlled
at the top level. You have all
the outputs and disturbances
necessary, so it should work.
But what about in a real-life
situation in which the
circumstances never recur. In
the hammering example, this
might be the only time in the
hammerer’s life that he is so
angry with his wife that he
has to hit something, and
doesn’t want to hit his wife.
How can the TCV be used in
that situation?And how do you use the TCVwhen control is poor? If you
get a poor compensation of the
disturbance by the output, how
do you know whether you
haven’t found the controlled
variable or you have found it
and the control system doesn’t
work very well?I think your statement issimply equivalent to saying
“PCT research is impossible”
which is something I don’t
believe, though I do believe
that the control of perception
accounts for what we see
people and other organisms do,
and that we should carefully
study by all available means
just how this works.Martin
BruceNevin
(2015.11.21.20:44
ET) to Martin
Taylor
BN: Thanksfor this nice
demonstration
of the
difficulty
with this
distinction
[between ECV
and p).
RM: I think
Martin aimed to
demonstrate that
controlling an ECV
is not equivalent
to controlling the
perception that
corresponds to
that ECV. But, in
fact, his
demonstration
doesn’t
demonstrate that
at all. What it
demonstrates is
that when you put
a bunch of
disturbances into
the feedback
connection between
output and input
you control
neither the ECV
nor p. To be
precise, the
disturbance
variables, d3 and
d4. enter the loop
after the output,
p2, and before the
input, (p4+d1).
See Martin’s
diagram below:
RM: When these
disturbances are
present the effect
of output (p2) on
input (p4+d1) is
constantly
changing. However,
if you remove
these disturbances
from the feedback
function control
is restored.
RM: In this
control loop p4+d1
is the controlled
quantity (q.i,or
ECV) and
g1*(p4+d1) is the
controlled
perception, p.
The only
difference between
q.i (the ECV) and
p is the scaling
factor, g1. But
variations in p
(p1) are perfectly
correlated with
variations in the
ECV (p4+d1); the
only difference
between p and ECV
is that the
former is measured
in neural firing
rate units and ECV
is measures in
physical units;
g1 is just a
scaling factor
that converts
physical units
into neural firing
rate units .
RM: I've
implemented
Martin’s model in
a spreadsheet, in
case anyone is
interested. It
allows you to see
how well the
perception, p1,
and corresponding
ECV (p4+d1) are
controlled when
the disturbances
to the feedback
function (d3 and
d4) are in or out
of the loop. When
these disturbances
are in, control of
both p1 and ECV is
poor but the
correlation
between variations
in p1 and the ECV
is 1.0; when these
disturbances are
out control of
both p1 and ECV
are excellent; and
the correlation
between p1 and ECV
is again 1.0.
…
RM:P I don't
know how people
got the idea that
PCT implies that
there is a
difference between
control of a
perception and
control of the
corresponding ECV.
But it's an
idea that is not
only wrong but one
that, if believed,
make PCT research
impossible.