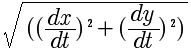[Martin Taylor 2016.08.09.12.36]
Yes.
Because if the power law holds for mouse movement, the sharpest
curve is at the top and bottom of the trajectory, but if it holds
for perception of the track, the sharpest curve is at the left and
right ends.
It's not derived from the power law. It asks whether the power law
holds for one or the other extreme possibility, or might perhaps
hold for some function of both (I hope the last is not the case). Or
it might not hold at all because something about the experiment
removes the critical factor on which the power law depends.
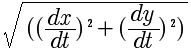
That's not what it is. Lots of people have done that. Some find a
1/3 power law, some a 1/4 power law and some find no power law at
all. But I don’t think there are enough studies to allow us to guess
from those difference what perception(s) is/are being controlled.
Are the the important controlled perceptions the same or different
when the results vary?
What this is, is a simple test. If (and only if) the power law in
some form holds either for mouse speed or for track speed, one could
then modify the experiment in various ways, looking for conditions
that lead to the three different possibilities (personally, I expect
that the viscosity effect will prove to be continuous, very high
viscosity leading to a near-zero power, very low viscosity to a
power near 1/3; but as I have said, my guesses are worth what you
pay for them.)
One caveat that carries a hint as to the controlled variable. One of
the power-law studies (I forget which one right at this moment)
showed that there is actually a lag that affects the computation of
the power law, and separately (maybe it’s in a different study)
there’s a difference in how fast the speed changes when going from a
sharp to a wide curve as compared to vice-versa. I expect that lag
to show up here, too. It’s a computational complication, but not one
that should affect the main result if either track perception or
mouse movement perception is the key power-law variable.
Don't forget to vary the absolute and relative orientations of the
ellipses between trials.
<img alt="" src="cid:part4.6D27F098.1427E5AB@mmtaylor.net" height="149" width="334">
And neither actually has to be an ellipse. I just drew ellipses
because it’s easy to draw them.
I don't predict at this point, though I have some intuition about
how the experiment might turn out. I ask Alex’s question, since the
answer has to start with whether we can find out what perception or
perceptions is/are being controlled that lead to the power law. One
possibility is the perception of the track to be followed, another
is some perception relating to the interaction of the muscle
movements with the track surface, which would have to be tested for
in a following experiment, while a third possibility is “neither of
the above” because the power law doesn’t appear for this experiment.
In the last case, we would have to search for something about this
situation that distinguishes it from the conditions in which the
data do show a power law.
When we have some clue as to what perception(s) is/are being
controlled, then and only then should we try to model and simulate
the various studies.
Martin
PS. Just FYI, when Bill programmed the basic software for my 1994
sleep studies, he included a 2D tracking study at Tom Bourbon’s
behest. But he didn’t include a model for that test as he did for
the other five, because he said he was not sure how to do it in a
way that would lead to results he could believe in. I have a feeling
that in addressing Alex’s question properly we might resolve Bill’s
dilemma.
(Attachment SqareCircleEllipsesSkew.jpg is missing)
···
[From Rick Marken (2016.08.09.0830)]
Martin Taylor
(2016.08.07.11.57)–
MT: This message is a start on trying to answer Alex's
question of July 6, rather than continuing to teach Rick
the difference between a formal parameter and something
that can actually be measured. As a reminder, here is
Alex’s original message.
Any
ideas why or how “the control of perception” may
give rise to this power law constraining geometry
and kinematics in humans, and now in fruit fly
larvae?
http://biorxiv.org/content/early/2016/07/05/062166
MT: Let's start with whether the 2/3 (or 1/3) power law
is a muscular output or a perceptual input phenomenon.
We can tease these apart by a modification of Powers’s
“Circle-Square” demonstration (p145ff and Demo 9.1 in
LCS III). In this demo you move the mouse to make a dot
that draws a white trace on the screen trace a red
square presented as a reference shape on the screen. But
the linkage between mouse and dot positions is such that
the mouse actually has to trace a circle in order to
draw the square.
MT: In the Powers demo, the subject moves the mouse very
slowly so as to make the square trace accurate (and so
as not to perceive the circle, at least not
consciously). We are interested in curvature, and the
speed with which moving objects like a tracing finger go
around curves of different radius of curvature, so we
can’t insist on that kind of accuracy. We want people
just to draw a shape. So let us have the perceptual
radius of curvature of the shape they draw be different
from the radius of curvature that the mouse follows.
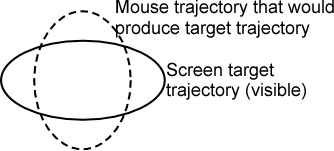
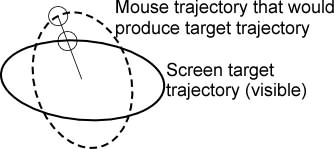
Show an ellipse as a reference trajectory on the screen
and scale the x and/or y of the mouse movement to the
cursor movement on screen. For example:
MT: The subjects should be able to do this quite freely
and smoothly if they aren’t told to be as accurate as
possible. If the power law has a perceptual basis, the
speed should be slowest around 3 o’clock and 9 o’clock,
and fastest at 12 and 6. If it is muscular, the opposite
should happen.
RM: The speed of what? Screen movement or mouse
movement?
And why do you predict this?
How is this derived from the power law?
And how do you measure speed at a particular location
on the curve?
It's great to see you proposing an actual empirical
test of the power law.
And I would like to carry it out.
But I need a little more detail about exactly what you
predict, and why (how is this prediction derived from the
power law).
Best
Rick
Of course, one would
want to make sure the ellipses were oriented differently
on different trials, not always at right angles to each
other
and probably not
usually with similar ratios of long to short axes. If a
power law holds, does it hold for speed around the mouse
trajectory or for speed around the screen trajectory?
If this simple experiment shows either that the power
law effect is totally muscular or totally perceptual,
further investigations, possibly even using
modifications of this are easy to imagine.
Martin
–
Richard S. Marken
"The childhood of the human
race is far from over. We
have a long way to go before
most people will understand that
what they do for
others is just as important to
their well-being as what they do
for
themselves." – William T.
Powers