[Martin Taylor 2014.03.01.12.09]
[A lot omitted here]
Since Rick brought up the “Behavioral Illusion” as the reason one
cannot measure the properties of a component of an active control
loop, I thought it might be a good moment to go a little deeper into
the reasons for the illusion than has been discussed here (at least
in recent years).
The “Behavioral Illusion” is the illusion that if you observe the
disturbance to an environmental variable and the behavioral output
that serves to counter the disturbance, the relation between them
tells you something about what is going on inside the organism,
whereas it actually tells you about the properties of the
environmental feedback pathway. Here’s a fragment of what Bill
Powers said in the Psych Review paper Rick referenced: …for an
ideal N [negative feedback. MMT] system, the output will vary as the
inverse g function [the environmental feedback function. MMT] of the
effect of the disturbance. Thus, the relationship between qd and qo
will be as precise and linear as the laws of geometric optics. The
organism function f, on the other hand, may be both nonlinear and
variable over time." The bit I quoted is a clean description of the behavioral illusion.
Often ignored when the words “behavioral illusion” are used in
discussion is that Bill correctly limited the statement to “an ideal
N system” – a perfect controller. When this criterion is ignored,
what is substituted is often something like “closed-loop control”,
which is contrasted with “open loop behaviour”. When the feedback
connection is broken, the relation between disturbance and output
depends as strictly on the properties of the organism as it depends
on the properties of the environmental feedback pathway in a perfect
controller.
Although Bill’s exact statement is often mutated into an all-or-none
contrast between “open-loop” and “closed-loop” conditions, that
black and white contrast is improper. There is a continuum of
possibilities between a physically unattainable “ideal N system” and
a perfect open-loop system. The better the control, the greater the
contribution of the environmental feedback pathway, and the less the
contribution of the properties of the organism to the relation
between disturbance and behavioural output.
Why should this be, apart from all the reasoning in the Psych Review
paper? I want to suggest that it is in part of my immediately
preceding message:
In saying you can say nothing at all about the the function from
measures of X and Y in the left-hand circuit, I was careful to
include the condition that you know nothing about Z. When, however,
the circuits are mapped into a segment of a control loop in which
the join of X and Z represents the environmental variable, you can
indeed say something about the relation of Z to X and Y. The rest of
this message is devoted to an analysis of what you can say about it,
and by implication what it means for psychological experiment.
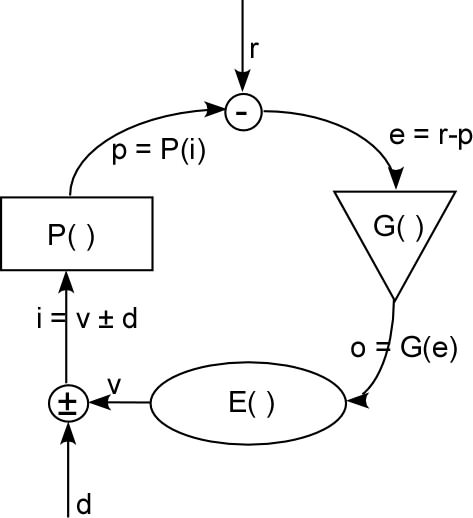
Here is a picture of a control loop (the same as in an earlier
message I just posted).
The question at issue is the relative degrees to which the
relationship between o and d is determined by E( ) on the one hand
and by P( ) and G( ) on the other. If it is 100% E( ), the
behavioral illusion is exact. If it is 100% P( ) and G( ) there is
no behavioural illusion at all. Between these extremes, both the
organism characteristics and the environmental feedback pathway
characteristics both contribute to the relationship.
I will assume r = 0 for simplicity of notation – it makes no
difference to the analysis.
o = G(e)
= G(r-p) = G(-p)
= G(-P(i))
= G(-P(v+d))
= G(-P(E(o) + d))
To go further, we have to make some extra assumptions, for example
that P and G are linear functions. This won’t be necessary in a
separate analysis that constitutes the second part of this message,
but we can use it for now.
o = G(-P(E(o)) + G(-P(d)
= -GPE(o) - GPd using GP as a short form for G(P( ))
and taking advantage of linearity to move the minus sign outside the
functions.
o + GPE(o) = -GPd
Now we need another assumption, that the function GP is invertible.
(GP)^-1(o) + E(o) = -d (Sorry about the awkward notion of
the inverse of GP)
Now, if E(o) = -d, control is perfect, and the form of GP is
irrelevant. This is the complete “Behavioral Illusion”. However, if control is imperfect, the imperfection is due to the
contribution of (GP)^-1, the organism characteristic. If E( ) is
known, then any deviation from perfect control provides information
about the organism characteristic.
···
A new month, a new subject line because this thread has drifted
far from the original subject line.
[Martin Taylor 2014.02.28.23.15]
RM: I went though the trouble to make this point, notbecause I think it will convince you, Martin; it looks
like you’re pretty committed to the idea that you can
measure the open-loop input -output characteristics of
a system when that system is in a closed loop.
Actually, I'm only convinced that when you do the analysiscorrectly, you get the correct result. And as a polemic device,
it’s quite interesting that you have now substituted “system” for
my “loop element” or “loop component” in asserting what I claim. I
am indeed “pretty committed to the idea that you can measure the
open-loop input -output characteristics of a circuit component
[not system] when that circuit component [not system] is in a
closed loop.” Note that “component of a control loop” was your own
wording in your original comment that started this argument
(quoted above).I say that if you have a circuit element whose behaviour you canassess by recording the covariation of its input and output (not
covariance), the assessment is exactly the same whether the
element forms part of a closed loop or is measured in isolation or
in any other network of connections.But I just thought I would put it out there for anyonewho wants to listen because I think it is the most
important (and revolutionary) contribution of PCT to our
scientific understanding of human nature. It’s an
extremely subtle and surprising discovery – and it could
only have been made by someone like Bill Powers, who not
only understood control theory but also how to apply it
correctly to human behavior. And it is the reason PCT has
had such a hard time getting any support from conventional
psychologists who, no matter what their theoretical
persuasion, believe with all their heart that even if
organisms are control systems you can learn about their
nature – the functions in them that convent sensory input
into response output – by measuring the relationship
between variations in input (created by varying
disturbances – independent variables) and variations in
outputs (dependent variables) under controlled conditions.
Bill Powers tried to explain why this was a futile belief
if organisms are closed -loop control systems. He
explained it in the 1978 Psych Review paper which is
reprinted in LCS I, the relevant section of that paper
being in the pages I referred to above: pp. 144-147 with
particular emphasis on p. 146.
There is both truth and error in this. See above. The error is notby Powers, who was talking about the behavioural illusion and the
fact that if you look at the disturbance and the output, what you
learn is the nature of the environmental feedback path, not the
properties of the organism. And that has nothing to do with the
topic under discussion.Martin
[MT] Here are two circuits:
` Z` ` |`` `` X------o---S---->function>------YX------S—>function>-------Y `
Now, given a lot of observations of X and Y, is it possible todiscover the nature of the function in each circuit? In theory one
cannot, because an infinite number of functions can give the same
set of {x,y} pairs, but in practice one can very often be correct
or at least make a good approximation with the right hand circuit.
Maybe Y = kX or Y = dX/dt or Y = 3X^3 + 2*X^2-X+4. Although
there are infinitely many functions that would give the same
results however much data you gathered, if the function is as
simple as these, enough data will allow you to get pretty close.On the other hand, one can say nothing at all about the left-handcircuit from observations of just X and Y, no matter how many
observations you make of X and Y, if Z is variable and you have no
knowledge of how it varies.You can, however, measure the function in both diagrams if,instead of measuring at X you measure at S.
Z
` |``
`` X------o---S---->function>------Y
X------S—>function>-------Y `
[From Rick Marken (2014.02.28.1850)]
On Thu, Feb 27, 2014 at 1:48 PM,Martin Taylor mmt-csg@mmtaylor.net
wrote:>> RM: You cannot measure the open loopbehavior of components of a control loop
>> when those components are still part of anactive control loop.
>> >> MT:That's a rather dramatic statement, andone I’ve never heard stated
>> other than by you. Could you present aproof of it?
> > RM: One proof is shown by the results of the“Nature of Control” demo, a
> JavaScript version of which is now availableat:
> [http://www.mindreadings.com/ControlDemo/BasicTrack.html](http://www.mindreadings.com/ControlDemo/BasicTrack.html) > > What you will find is that the correlationbetween input (Cursor, C) and
> output (Mouse, M) is typically close to 0. > MT: Could you explain the relevance of thisfact to the point at issue?
RM: The 0 correlation between input (i) and output(o) in a control task shows that the measured
relationship between input and output does not
reflect what we know (from modeling) to be the
actual “open loop” input-output component of the
control system, which is something like o = k(r-i)
with k considerably greater than 0. But you can’t
get a measure of this open loop component when it is
still part of a control loop. What that component of
the control loop looks when measured in the intact
control system looks (per the tracking demo) like o
= 0 (i) rather than what it actually is, o = k(r-i)
.