Martin
···
From: Martin Taylor (mmt-csg@mmtaylor.net via csgnet Mailing List) [mailto:csgnet@lists.illinois.edu]
Sent: Saturday, August 04, 2018 6:04 PM
To: csgnet@lists.illinois.edu
Subject: Re: Bogus mathematics, (was Re: L’état de PCT, c’est moi (was …))
[Martin Taylor 2018.08.04.11.45]
On 2018/08/4 4:05 AM, Adam Matic (adam.matic@gmail.com via csgnet Mailing List) wrote:
Thanks, Adam, for this message.
For the time being I have personally given up on trying to explain the issues to Rick, and on reading his messages on the topic, at least until I think of a new way to address the actual problem. I hope anyone on CSGnet interested in the curvature-velocity issue has had enough time to see through the anti-scientific nonsense he keeps repeating on this issue – not to mention the self-contradictions and the lies about what is being criticised,
HB : Nice description of how Ricks’ hierarchy works. I’m glad that number of members that perceive Ricks’ manipulations grow. Â
MT : …like the one near the end of your quote.
HB : I don’t beleive that Rick in his allmighty  egoism understands what he is doing to people. He seems to be insesible for other oppinions which are really scientific. I wonder when those who are responsable for »scientific«  purity of CSGnet will understand that Rick is just ordinary manipulator who is functioning perfectly in accordance to definition of PCT and diagram (LCS III). Just keeping his internal variables in predefined state with the highest possible »gain«. But human beings are more than that. But to understand this Rick has to understand how organisms and consequentially hierarchy function. Oh I forgot he’ll be lecturing about hierarchy on CSG meeting so he »obviously understands« it.
MT : As for “PCT says”, when Rick says it, it is accurate, since as he has told us more than once, “PCT, c’est moi”.
HB : Right. Rick privatized »PCT« like it’s his theory although real owners (I assume) are Powers ladies. So I’m not sure whether they and Rick has some agreement that he »borrowed« PCT for certain period of time.
You and me and some others showed and proved Rick many times that his PCT is turned arround. It’s  »Perception : The Control of Behavior«. The central problem is that Rick never proved that behavior can be controlled. Anyway he is talking about RCT (Ricks’ Control Theory) and it seems that he understands well what mess and confussion he is provoking on CSGnet.
RM earlier : I’m afraid I’ll be staying here on CSGNet. But I agree that people on CSGNet seem to like your version of PCT better than mine.
HB : It’s not only Rick who is affraid of staying on CSGnet, there are also others who are affraid for the future of scientific understanding of how organisms function.
Despite the »fact« that Rick understands that his »version« of PCT which is RCT is bad, he still incite to manipulations and lies and so on…  He probably  thinks it’s his »moral obligation« to »protect« his quite useless work on PCT with any means that is possible in the style that »Means are justifying goal achievement«. Â
MT : Meanwhile, the rest of us can continue to work on the science involved with the control of perception, and not worry about whether the science is in accord with what “PCT (Rick) says”.
HB : This is great proposal Martin.
Boris
Martin
[From Adam Matic]
My bet is you still don’t know the difference between common uses of trajectory and path, Rick. Other that that, you keep saying mutually conflicting statements, or you keep flipping between two extreme positions on some issues. Your statements reveal confusion, but your are still very confrontational and trying to sound authoritative. That is just silly. You’re on fast track to being a crank scientist. However, given your modus operandi of giving strong statements, then going back on them after a few days (weeks, months?) when you realize your mistake, you just might come back from the dark side. That is probably Martin’s hope too.
RM: The math is irrelevant to seeing that the power law is a side effect of control. The power law is precisely analogous to the tangential velocity profiles discovered by Atkeson and Hollerbach and discussed by Bill Powers in the posts from the CSGNet archives that are copied below. Like the power law, tangential velocity profiles are an “invariant” side effect of making controlled movements of a limb. These side effects become a behavioral illusion when they are taken to tell us something about how the observed movement was produced.
AM: Yes, the power law is analogous to bell-shaped velocity profiles. They are not a controlled result (as Bill says), just like power law trajectories are not controlled results (this is my hypothesis). You, on the other hand, claim that power-law trajectories are a controlled result. You also published a model of ellipse tracing which has a 2/3 power law trajectory as the reference trajectory. That is where you are conflicting with yourself - if the trajectory is a side effect then it is not controlled. If it is controlled, then it is telling us that the reference trajectory is also a 2/3 power law trajectory.
AM: The behavioral illusion is one of the issues you have flipped up and down several times, I’ll number it. After publishing two papers saying 1) the power law is behavioral illusion; sometime in May on csgnet you had no problems saying that 2) the “power law is not a behavioral illusion as in Powers(1978)”, then 2) “it is maybe the illusion of control”, then 3) maybe we should just stop telling people about this illusion business; and again back to 1) it is a behavioral illusion.
According to the 1978 paper, a behavioral illusion happens when someone mistakes a correlation between a stimulus and a response for a causal relationship. No one is taking the instantaneous curvatures and velocities of the response to be causally related, those are both properties of the response. There are hypotheses on causal role of the brain in the power law (the reference trajectory is a power law trajectory) and there is the unrelated causal role of the shape of the stimulus and the exponent of the power law (you get different exponents if you draw different shapes).
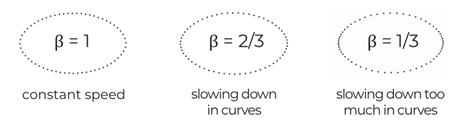
The math you and Shaffer present on the meaning of the power law exponent is based on some serious misunderstanding. The exponent of curvature - angular velocity power law just tells you how much an object traveling along a path is slowing down in corners. If the exponent is 1, the speed is going to be constant all over. If the exponent is lower, such as 2/3, it means the object is going a bit slower in the corners than in the straight parts. If is still lower, it means the object is slowing down a lot in the corners, and speeding up a lot in the straight parts. It is complete nonsense to speak about a “true exponent” (see, no need for math to show your bogus logic).
RM: So it is rather ironic that people who are supposed to be experts on PCT and the behavioral illusion have succumbed to that illusion so thoroughly that they are trying to use math to show that an obvious example of a behavioral illusion – the power law – is not an illusion at all.
AM:
It is ironic that you keep saying “PCT says” and then present your own bogus hypotheses. There is nothing in PCT that says the power law is a behavioral illusion or that the research on the power law is based on a mistake of confusing correlation for a causal relationship. You are saying that. And you are kinda shit at math, as you have been before, but you seem to have been quicker to admit it and did not make grand claims based on your “calculations”. Maybe it was Bill who corrected you when you strayed over to crank territory, now you are just pushing forward.
Best,
Adam
On Sat, Aug 4, 2018 at 9:15 AM Richard Marken csgnet@lists.illinois.edu wrote:
[Rick Marken 2018-08-03_22:07:26]
[Martin Taylor 2018.07.30.01.08]
On 2018/07/29 7:38 PM, PHILIP JERAIR YERANOSIAN (pyeranos@ucla.edu via csgnet Mailing List) wrote:
PY: In what way do you get from these equations:
to this equation:
PY: I see that R = V^3/what looks like some chain rule expression.
Can you please explain how you see V^3 in the denominator?
MT: You are going the wrong way around, because any expression for R must be expressed in spatial variables alone. The point you want is to demonstrate that this is the case for the expression that starts with velocities and accelerations, which are expressions in space and time. The usual way to get there is to start from the expression in s, x, and y as did Viviani and Stucchi (whom Gribble and Ostry used as their source – Marken and Shaffer used Gribble and Ostry to justify their equation) and work from there to the equation labelled (3). But I’ll work it backwards for you.
RM: The math is irrelevant to seeing that the power law is a side effect of control. The power law is precisely analogous to the tangential velocity profiles discovered by Atkeson and Hollerbach and discussed by Bill Powers in the posts from the CSGNet archives that are copied below. Like the power law, tangential velocity profiles are an “invariant” side effect of making controlled movements of a limb. These side effects become a behavioral illusion when they are taken to tell us something about how the observed movement was produced.
RM: The mathematics presented by Dennis Shaffer and I shows why the invariance of power law is found for many controlled (and uncontrolled) movements. Powers’ Little Man model of movement production shows why invariant velocity profiles are found for controlled movements. (note in [Bill Powers (931029.0750 MDT)] where Bill says: “The velocity profiles are individually scaled both as to amplitude and duration in order to generate the congruence that the authors found. If you do this for the joint angular velocity profiles in Little Man V2, you will find similar invariances, even though there is nothing computing them” (emphases mine–RM)).
RM: Even if the math used to explain the invariance of the power law were wrong (which it’s not) it is still easy to see that the power law is a side effect of control and, to the extent that it is taken to tell us something about how the observed movement was produced, it is a behavioral illusion.
RM: So it is rather ironic that people who are supposed to be experts on PCT and the behavioral illusion have succumbed to that illusion so thoroughly that they are trying to use math to show that an obvious example of a behavioral illusion – the power law – is not an illusion at all.
Best
Rick
=====================================================
[From Bill Powers (931029.0750 MDT)]
Greg Williams (931028) –
Very nice job in picking up the quote on motor schemas. Don’t
forget to include William James – the constancy of ends and the
variability of means. All this shows that the problem has been
known for a very long time (100 years), but that the solution has
eluded a continuing search.
The critical misdirection is contained in
Thus whatever is learned and stored in long-term memory cannot
be a specific set of muscle commands but must represent a more
generic or general set of specifications of how to reach the
desired goal.
Behind the idea of “specifications of how to reach the goal” is
still a picture of direct causality: the specification is for
how to reach the goal, instead of what goal to reach. You can
see this same idea in Atkeson and Hollerbach:
"A strategy for gaining insight into planning and control
processes of the motor system is to look for kinematic
invariances in trajectories of movement. The significance of
straight-line movements is that they imply movement planning at
the hand or object level." (p. 2318)
In the discussion:
"Taken together, shape invariances for path and tangential
velocity profiles indicates that subjects execute only one form
of trajectory between any two targets when not instructed to do
otherwise. The only changes in the trajectory are simple scaling
operations to accomodate different speeds. … Different subjects
use the same tangential velocity profile shape." (pp. 2325-6).
And making the problem even clearer:
"A number of issues remain with regard to these dynamic scaling
results. How are the initial torques for the first movement
generated? If the motor controller has the ability to fashion the
correct torques for one movement, why does it not use this same
ability for all subsequent movements rather than utilize the
dynamic scaling properties? Among the possibilities we are
considering, the first is a generalized motor tape where only one
movement between points need be known if the dynamic components
in Equation 6 are stored separately. … A second possibility is
a modification of tabular approaches (Rabert, 1978) where the
dimensionality and parameter adjustment problem could be reduced
by separate tables for the four components in equation 6." (p.
2327).
The only possibilities being considered are those that involve
open-loop generation of the torques that will produce a pre-
planned trajectory. “Equation 6” is an equation expressing joint
torque as a nonlinear function of scaling factors applied to
torques previously produced for a known movement. As noted above,
the problem is how the torques for the known movement are
generated in the first place. This problem is not solved. What
the authors hope for is that by finding invariants such as
velocity profiles, they will be able to deduce a motor program
that will produce constant results in object space even when
variations in torque are required.
They simply haven’t got far enough into the problem to see that
this quest is hopeless. If they did manage to come up with a
motor program that could realistically create several
trajectories of hand movement between different pairs of points,
they would then have to ask how this can work with different
loads. If they solved that problem, they would have to explain
how the trajectories are produced when the loads are vary
unexpectedly and the muscles progressively fatigue. And then they
would have to explain how the right torques can be produced under
varying loads (such as the varying friction between pencil and
paper) and with fatiguing muscles, when the task is to write the
subject’s name. And then they would have to explain how a subject
can accomplish the same movements under the same uncertain
conditions for the tip of a pointer held in the hand. In truth,
they are extrapolating a long way ahead, and predicting success,
when they have not even found the simplest motor program of all:
that for moving quickly between two points under undisturbed
conditions. Their projected work simply expresses faith that
somehow the require movements in object space can be generated by
a clever enough motor programming device – without ever taking
feedback into account, the feedback both kinesthetic and visual
that is known to exist and that is known to be essential for
skilled performance.
There is an explanation for the observed invariances of velocity
profiles that Atkeson and Hollerbach never consider: these
invariances might simply be the natural outcome of physical
processes of control. There might be no need at all for the motor
program to precompute them. The velocity profiles are
individually scaled both as to amplitude and duration in order to
generate the congruence that the authors found. If you do this
for the joint angular velocity profiles in Little Man V2, you
will find similar invariances, even though there is nothing
computing them. It just happens that when a control system is
given a step-change of reference-signal, the trajectory of the
controlled variable naturally scales up or down so that the
velocity rises and falls along the same generic curve. This is
purely a consequence of the mathematical relationships of control
and the passive dynamical properties of the arm; nothing is
acting to make sure that the trajectory follows any particular
path. The trajectory is a side-effect, not a planned movement.
Evidence of trajectory planning would appear only if the actual
trajectory departed from the one that can be explained as a step-
change in the reference signal of a control system from one fixed
value to another. For example, one can easily move a finger from
one point to another along a semi-circle or an S-shaped curve.
That requires a “program” of velocity or position reference
signals. But it still doesn’t require precomputing torques.
The key idea to look for in all these sources is how the authors
propose to account for the forces that create movements. It’s
clear in Atkeson and Hollerbach that the torques are going to be
computed so as to have the required object-space consequences and
that proprioceptive and visual feedback are not considered. All
approaches that propose to use inverse kinematic or inverse
dynamical computations are also attempting to solve the problem
open-loop. In all such approaches, the key idea that is missing
is comparison of the observed consequences with the desired
consequence in real time as the means of producing the required
output signals.
Atkeson, C. G., and Hollerbach, J.M.; Kinematic Features of
Unrestrained Vertical Arm Movements. The Journal oif Neuroscience
5, No. 9, pp. 2318-2330. Sept. 1985.
Best,
Bill P.
[From Bill Powers (950527.0950 MDT)]
Just got back from seeing our daughter Barbara off in the start of the
Iron Horse bike race, Durango to Silverton. The length is 45 miles, the
total climb over two main passes is 5500 feet (the highest pass, Molas,
is about 11,000 feet). Last year (her first, at age 35) she did it in
4:20; this year she hopes for under 4:00. The pro winning time last year
was 2:10. She should be about halfway right now, starting the four-mile
climb to Coal Bank Pass (2500 foot climb to over 10,000 ft). Go Bara!
Rick Marken, Bruce Abbott (continuing) –
===================================================
When you push on a control system, it pushes back.
===================================================
RE: trajectories vs. system organization
In a great deal of modern behavioral research, trajectories of movement
are examined in the hope of finding invariants that will reveal secrets
of behavior. This approach ties in with system models that compute
inverse kinematics and dynamics and use motor programs to produce
actions open-loop. These models assume that the path followed by a limb
or the whole body is specified in advance in terms of end-positions and
derivatives during the transition, so the path that is followed reflects
the computations that are going on inside the system.
It is this orientation that explains papers like
Atkeson, C. G. and Hollerback, J.M.(1985); Kinematic features of
unrestrained vertical arm movements. The Journal of Neuroscience 5,
#9, 2318-2330.
In the described experiments, subjects move a hand in the vertical plane
at various prescribed speeds from a starting point to variously located
targets, and the positions are recorded as videos of the positions of
illuminated targets fastened to various parts of the arm and hand.
The authors constructed a tangential-velocity vs time profile of the
wrist movement for various speeds, directions, and distances of
movement. They normalized the profiles to a fixed magnitude, then to a
fixed duration, and found that the curves then had very nearly the same
shape. Using a “similarity” calculation, they quantified the measures of
similarity.
They were then able to compare these normalized tangential velocity
profiles across various directions and amounts of movement and show that
the treated profiles were very close to the same. They conclude:
Taken together, shape invariance for path and tangential velocity
profile indicates that subjects execute only one form of trajectory
between any two targets when not instructed to do otherwise. The
only changes in trajectory are simple scaling operations to
accomodate different speeds. Furthermore, subjects use the same
tangential velocity profile shape to make radically different
movements, even when the shapes of the paths are not the same in
extrinsic coordinates. Different subjects use the same tangential
velocity profile shape.
… this would be consistent with a simplifying strategy for joint
torque formation by separation of gravity torques from dynamic
torques and a uniform scaling of the tangential velocity profile
… (p. 2325)
… if the motor controller has the ability to fashion correct
torques for one movement, why does it not use this same ability for
all subsequent movements rather than utilize the dynamic scaling
properties? Among the possibilities we are considering, the first
is a generalized motor tape where only one movement between points
must be known if the dynanmic components in equation 6 are stored
separately…A second possibility is a modification of tabular
approaches [ref] where the dimensionality and parameter adjustment
problem could be reduced by separate tables for the four components
in equation 6. (p. 2326)
This paper was sent to me by Greg Williams as a source of data about
actual hand movements, for comparison with the hand movements generated
by Little Man v. 2, the version using actual arm dynamics for the
external part of the model. The model’s hand movements were, as Greg
will attest, quite close to those shown in this paper, being slightly
curved lines connecting the end-points. Forward and reverse movements
followed somewhat different paths, and by adjustment of model parameters
this difference, too, could be reproduced.
What is interesting is that the fit between the Little Man and the real
data was found without considering tangential velocity profiles or doing
any scaling or normalization. In other words, the invariances noted by
the authors were simply side-effects of the operation of the control
systems of the arm interacting with the dynamics of the physical arm. In
the Little Man there is no trajectory planning, no storage of movement
parameters, no table-lookup facility, no computation of invariant
velocity profiles. The observed behavior is simply a reflection of the
organization of the control system and the physical plant.
The path which Atkeson, Hollerbach (and many others at MIT and
elsewhere) are treading is a blind alley, because no matter how
carefully the observations are made and the invariances are calculated,
there will be no hint of the control-system organization, the SIMPLE
control-system organization, that (I claim) is actually creating the
observed trajectories. No doubt a sufficiently complex trajectory-
control model, with just the right tables of coefficients and velocity
profiles, would ultimately be able to match the behavior. But this line
of investigation, with its underlying assumptions, will never lead to
the far simpler and anatomically correct PCT model.
In terms of the current discussion on the net, the observations made by
the authors were interesting as checks on the model, but were actually
irrelevant to what the control systems were doing. The control systems
(the first two levels of the Little Man model) controlled only three
kinds of variables that underlay the perceptual signals: angular
positions, angular velocities, and angular accelerations. They received
no information about wrist position in laboratory space. They contained
no provision for computing tangential velocities, or for computing
positions of points on the physical arm in space, or for computing
space-time invariants. The behavior of the control systems, in other
words, took place in a proprioceptive perceptual space that no outside
observer could see. In order to translate from this perceptual space
into variables that were observable, the computer program generated the
resulting arm positions and plotted them in a form suitable for visual
inspection. So a side-effect of the actual control process was presented
for comparison with a corresponding side-effect of the real control
process, as visible to an outside observer.
The approach of Atkeson and Hollerbach appears in many guises. We have
already talked about the apparent scaling and normalization of
trajectories seen when two hands move rapidly and simultaneously to
targets at different distances. In operant conditioning experiments, we
have seen how the control of reinforcement by behavior is obscured by
the fact that variations in behavior tend to stabilize reinforcement
rates, thus making reinforcement rate appear to be the independent
variable.
We have also seen a few – a very few, so far – studies in which the
PCT orientation was used, Srinivasan’s being the most recent. What is
the difference? I think the difference is in whether the emphasis is on
seeing the behavior from the behaving systems’s point of view, as best
we can imagine it, and seeing it strictly from the human observer’s
point of view.
From the human observer’s point of view, it seems that we must account
for the detailed movements and physical interactions that are seen to
occur. This leads to trying to find invariances or striking mathematical
regularities of some sort in the observed behaviors. It leads to
imagining an internal system that is producing explicitly what we are
observing; if we observe a trajectory, there must be some generator that
is specifically calculating that trajectory.
But from the behaving system’s point of view, we can consider only the
information that is available to the behaving system; we must look for
our explanations there. The trajectories of movement that result from
the system’s operation are basically side-effects; they are not planned
and they are constant only in a constant environment. Furthermore, they
are unknown to the behaving system and play no part in the production of
behavior. We can deduce from the model of the behaving system what the
observable side-effects would be in a given environment, and so can
compare those side-effects with our external observations of the
behavior. But our explanation of the behavior is not based on those
side-effects.
Most important, when we simply describe behavior as a sequence of
physical happenings and relationships, we have no way of knowing whether
we are describing controlled variables or side-effects. When we see a
fly landing on a ceiling, it is perfectly possible that NOT A SINGLE
ASPECT OF WHAT WE SEE is perceived and controlled by the fly. When we
see the fly extending its legs just prior to landing, the fly may have
no perception of the configuration of its legs; to the fly, all that is
controlled may be two or three joint-angle signals, not even identified
by the fly as representing joint angle. When we see the wings stop
flapping, to the fly all that may be controlled is a sensation of
vibration. When we see the fly’s body making a steep angle with the
surface, the fly may simply be experiencing a visual signal indicating,
as Rick guessed, a gradient of illumination or texture. Not one of the
variables we are observing may ever appear in the ultimate model of the
fly’s internal organization, just as in the Little Man the actual arm
configuration and hand position never appear in the model of the first
two (kinesthetic) levels of control. Once we have the right model, we
can always compute how its operation will appear to an observer who is
focusing on various side-effects of the actions. But the model itself
says nothing about those appearances, and makes no use of them.
Best to all,
Bill P.
–
Richard S. Marken
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
–Antoine de Saint-Exupery