[Martin Taylor 2017.09.30.15.18]
[From Rupert Young (2017.09.30 20.10)]
(Martin Taylor 2017.09.30.12.32]
[From Rupert Young (2017.09.30 14.00)]
That sounds fine for an individual continuous control system,but how about when it requires changing (switching)
control systems. For example, to control car speed we have to
learn to switch between control systems for brake and
throttle. We learn this pretty quickly so it seems unlikely to
part of the same process (of varying the parameters of
control), so what is involved in learning in this case?Rupert, what you say may be true of linear systems, butnon-linear systems with feedback can have abrupt changes of
effect with continuous changes of parameters. Technically, they
show “catastrophe” like this fold catastrophe (which illustrates
perception, but the fold idea is the same for output).Yes, that's a good point. Is this case showing that the output ofa perceptual function, of two linear inputs, is non-linear? Would
the output case be applicable to the brake/throttle example?
No, that's not the context of this picture. The context is that of a
feedback loop with at least some non-linear components that limit
their output, not necessarily a control loop. Perceptual functions
are often (and probably always) non-linear, approximating
logarithmic quite often. I have a couple of times on CSGnet proposed
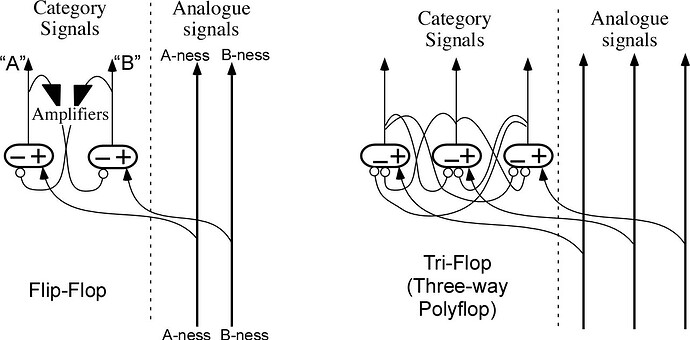
a flip-flop type of circuit to perform category perception, and I do
so again. The figure also shows an extension to what I call a
“tri-flop”, a circuit we used a lot in hardware form for auditory
experiments around 1970.

The same kind of excitatory-inhibitory connection pattern can be
extended to polyflops with more than three possible category
outputs. Each category output is fed back to the input of all the
other possibilities as an inhibitory signal, allowing only one of
the outputs at a time to be strongly positive, and sustaining that
output while the analogue balance changes until one of the other
excitatory analogue inputs becomes strong enough to overcome the
inhibition, at which point there is an abrupt switch to a different
category output. Polyflop connections create labelling, as suggested
by the dotted interconnections between the sound and shape polyflops
in this diagram, which shows how a perception of shape “A” is
facilitated or possibly evoked by perception of sound “eh” and
vice-versa. Each is a label for the other.

The labelling property can be extended to multiple perceptual
classes in which perception of a member of any one polyflop group or
category can facilitate (or evoke) corresponding members of multiple
others, while at the same time the groups as categories can have the
same kind of mutual inhibition as suggested by the above two
figures. If, say, the shape “a” is perceived, so is “Lower case”,
which tends to inhibit “Greek” and “CAPS”, which don’t co-occur with
“a”, but not necessarily “Sounds” and “Grades”, which often do.

When there is a decision to be made, usually some kind of category
is involved, though it could be a greater than - less than
relationship, which we discussed in a different thread not long ago
in conjunction with positive-only neural signals. Both wind up with
the distinct possibilities being carried on different “wires”, and
thus being available for possible sending of output to different
lower-level perceptions.
The same kind of flip-flop or polyflop circuit as in the above
figures (turned upside down for viewing) might implement choice of
output means, as, say, between walking, cycling, or taking the car
or a bus to control a perception of one’s location with a reference
that differs from one’s current location. In other words, as
“category perception” it implements perceptual decisions, and as
“execution choice” it implements performance decisions.
The other possibility is the Powers idea that references are theoutputs of associative memories addressed by the current outputs
from higher-level control units (or, I would suggest, by a
vector of current error values). That, too could change abruptly
with a continuous change of perceptual values.I'd been considering this, but didn't see how a weight-adjustingreorganisation process would account for that.
No, it wouldn't, but if you remove "weight-adjusting" the
reorganization process could.
Itwould seem to me that memorising requires an instant change in the
state of the control system (or perhaps locking in the current
state), as opposed to gradual changes in parameters (gain, e.g. as
in arm reorg in LS3). For example, with my tea example, the first
time you drink tea you may add sugar, bit by bit, repeatedly
tasting, to control your desired perception of sweetness. It would
be laborious, and impractical, if you had to repeat his process
every time you drank tea, so you remember your perception of
adding three spoonfuls, say. Next time you drink tea you control
the desired sweetness by adding three spoonfuls of sugar without
having to taste it.This doesn't seem like (the same) reorganisation to me, butinstant storage of a perception value, when the error is zero, to
be later used as a reference. Any thoughts on this?
Bill mused a bit about this, I don't remember whether on CSGnet or
just in private communication with me. I can’t remember ever
reaching a solution that could be justified by Ockham’s Razor
principles. Here’s what I think at this moment.
The problem isn't in using existing address-output pairs to produce
a new vector of reference levels to fit a previously encountered
situation. That’s easy. The problem is in choosing when to install
new address-output pairs and what should be their content. At the
moment I think that the word “choosing” in the last sentence leads
us astray. It follows the “reinforcement learning” tradition rather
than the PCT “reorganization” or “winter-leaf” tradition. If you
treat the issue not as one of installing a novel association at some
defined moment, but as changing associations all the time, but more
slowly as some criterion approaches an optimum, some of the problem
goes away.
Looked at as an aspect of normal reorganization, the current vector
of perceptions is always available (and being stored) as a possible
later reference vector, and the current set of higher-level outputs
is always available as a possible later address vector. But those
values keep changing if control is not good, in the usual manner of
reorganization, and change more slowly, if at all, when control is
good and the other intrinsic variables are near their genetic
reference values. So when they are used to provide reference values
for lower levels on a later occasion, the values returned will be
those that worked well before, if they haven’t been modified by a
similar process when controlling a related higher-level variable in
a slightly different situation.
With this conception, the reorganization of association vectors is
very like the reorganization of inter-level analogue links: “if it
ain’t broke, don’t fix it” together with “if it’s not working, try
something else” (also together with, of course, the control motto
“if what you are doing is working but needs more effort, do more of
it.”).
As is also true of the standard version of reorganization by
changing link connections and weights, the exponential explosion of
dimensionality requires modularization. Not all current perceptions
or outputs are likely to be affected by any particular association
reorganization. I don’t want to mix this message with speculation on
how modules form, but they must. I can suggest, however, that the
polyflop circuits above (upside down) could be an implementation
mechanism for the associative memory, and they inherently generate
the required modularity, since the mutual inhibitions appear only
when categories within a polyflop group seldom if ever co-occur, but
occur usually in similar perceptual (or output) contexts.
One would not expect many of the mid-level control loops used in,
say, boiling an egg, to be implicated in, say, reconciling a
chequebook or transplanting a flower. The lower level sensor and
muscle systems, however, would be used in all these different
circumstances, so they must be generalists with not much, if any,
modularity.
I don't know if this is very useful, but it does seem to place the
development of associative memories in the frame of PCT
reorganization, rather than the frame of reinforcement theory, which
I think simplifies it within standard Perceptual Control Theory, and
thereby simplifies PCT itself.
Martin