[From Bruce Abbott (2016.09.15.1100 EDT]
I thought this might be a good time to show geometrically how the curvature of an arc at a given point P is derived. The figure below shows a curvy black line to which has been fit an “osculating circle” – a circle whose curvature is a good approximation to the curvature of the line at point P.
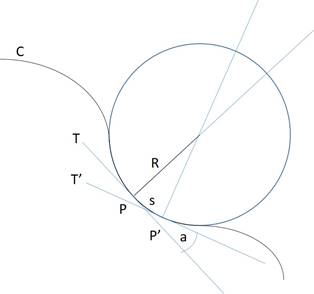T is the tangent to the circle at point P. At a right angle to this tangent line is the circle’s radius, R.
If we move along the line from P to point P’, we have covered a distance s along the arc of the line. T’ is the tangent to the circle at P’. Notice that the angle of the tangent has changed relative to its angle at point P. This change in angle is labeled a in the figure. How much this angle changes from P to P’ depends on (a) the distance along the arc between P and P’, and (b) the radius of the osculating circle, R. If we divide a by s, we get the change in tangent angle per unit distance, and this ratio will then depend only on the radius of the osculating circle: The larger the radius R, the smaller will be the change in angle a.
Now imagine removing the osculating circle from the diagram, leaving everything else in place. This is the situation in which we do not know the radius of the circle but must find it based on the curvature. The radius line extends at a right angle from the tangent line, but we do not know its length. However, given that we have two points, P and P’, we can find the radius – it will be the point at which the two radius-lines cross.
In the context of the present debate, it is important to note that there is no mention of time in this derivation. Curvature and the radius of curvature do not depend on distance traveled per unit of time, but rather on the rate at which the tangent angle changes per unit of distance along the perimeter of the circle.
In research on the power law, however, we have a curvy line being navigated at some velocity V, which may be constant or may vary from one moment to the next. We can measure this velocity along the path at regular time intervals. If V is being measured, say, every .01 seconds, then we can divide the velocity by .01 seconds to get the distance traveled between the initial position of the moving point, P, and its new position, P’. We can also use the changes in velocity and acceleration along the X and Y directions to estimate the change in the angle of the tangent line. When we take the ratio of these factors, time drops out and we are left with a pure measure of distance: the radius R of the osculating circle. This makes sense, because neither the radius of that circle nor its curvature should depend on the velocity with which the figure is drawn. These are pure measures of static shape.
I have presented this analysis in terms of moving a distance s along the line. Imagine that we shorten that line and compute the curvature again, and we keep doing it until we have almost an infinitely short distance, and associated with it, an almost infinitely small change in angle. Unless we are dealing with a straight line, we will be approaching a value for R or C “at the limit.” Using the calculus of differential equations, we can find these values as the distance s “goes to zero.” These will be our values for R and C. (R is just 1/C).
Because the formulas for curvature and radius of curvature are based on geometric properties that have nothing to do with the passage of time, it is simply not correct to solve the formulas for velocity (distance/time) and conclude that the changes in velocity over time must depend on curvature (or radius of curvature). Moving velocity to the left side of the equation leaves the other time-based factor (what Rick calls D) behind. If you regress V on D and R, you can only recover the original formula that was used to compute R. This will tell you nothing about how V and R are related in the observations. Furthermore, leaving D out of the equation just removes a crucial part of the formula, which together with V removes time from the computation. How the numerator and denominator change together is what determines curvature; curvature (or radius of curvature) does not determine velocity.
Bruce
