Continuing the discussion from Collective control as a real-world phenomenon:
Eetu said:
This quote from Powers seems really strange for me, especially the last sentence (italics by me):
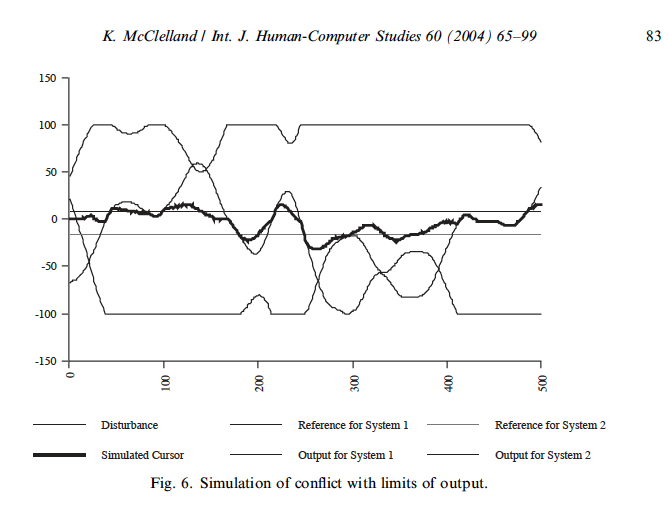
These two outputs, if about equal, will cancel, leaving essentially no net output to affect the controlled quality. Certainly the net output cannot change as the “controlled” quantity changes in this region between the reference levels, since both outputs remain at maximum.
This means there is a range of values over which the controlled quantity cannot be protected against disturbance any more. Any moderate disturbance will change the controlled quantity,…I think this should mean that if there is an arm wrestling and a tug of war going on between equally strong participants and the situation is frozen so that both participants pull or push with their full strength but the flag or clasped hands don’t move, then in that situation it should be possible for you (if you could do it invisibly) to move the hands or the flag easily back and forth. I really can’t believe this. Has anyone ever tried?
Actually, I did try it last Saturday when I was having dinner with Gary Cziko and his wife. Gary and I arm wrestled while his wife applied gentle disturbances to the position of our clasped hands and they seemed to move easily. So my description, based on Bill Powers’ description, of a Dead Zone that exists when there is a conflict, seems to have been correct. But Kent argues that there is no Dead Zone in his models of conflict. If this were true then Bill’s (and my) description of the Dead Zone was incorrect.
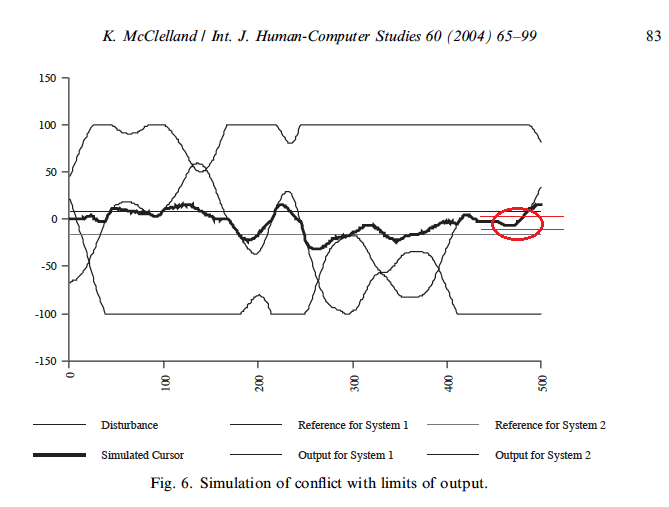
Kent presented the following data as evidence that there is no Dead Zone:
But this is not a proper test for the existence of a Dead Zone. The fact that the conflicted systems correct for disturbance even when limited in the maximum output they can produce does not disprove the existence of a Dead Zone. The Dead Zone is defined as a range of disturbance amplitudes that will not be resisted by control systems in conflict – a virtual control system - but will be resisted by an equivalent unconflicted control system.
I have developed a spreadsheet model that demonstrates the existence of a Dead Zone that exists when two control systems of equal strength – in terms of maximum possible output – are in conflict and does not exist for an equivalent unconflicted control system.
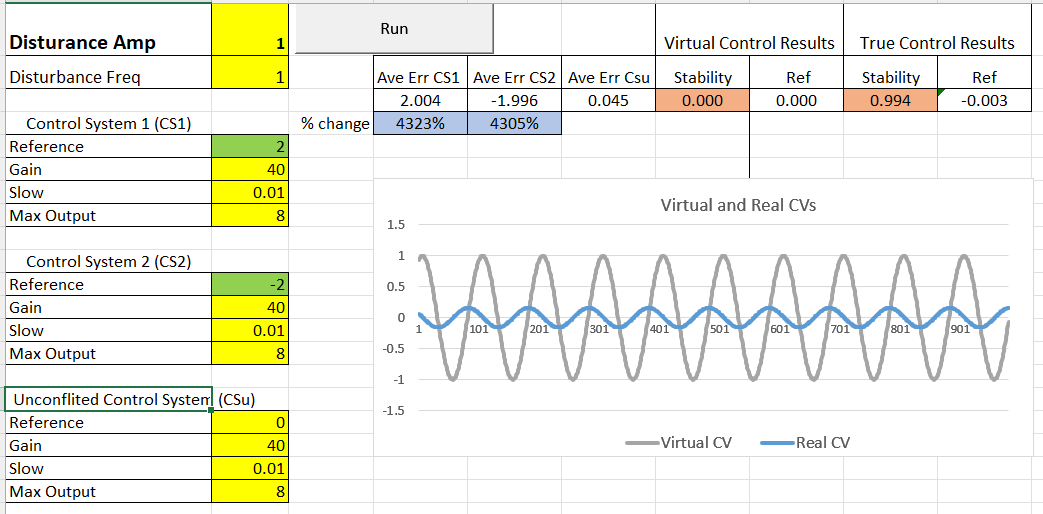
The spreadsheet opens to this display:
On the left, highlighted in yellow and green, are cells where you can enter values for the amplitude and frequency and frequency of the sine wave disturbance, and parameters for two control systems that are in conflict (CS1 and CS2) and an equivalent unconflicted contol system (CSu). The control systems are controlling the position of the same cursor in a tracking task; so the controlled variable is the same for both systems: cursor position.
To begin using the spreadsheet start by leaving all control system parameters as they are. The control systems are set to have equal strength in terms of Gain and Maximum Output. The conflicted control systems (CS1 and CS2) have references of 2 and -2, respectively, and the unconflicted control system (CSu) has a reference of 0, which is equivalent to the virtual reference of the two conflicted systems. . The disturbance is a sine wave with amplitude set to 1 unit and a frequency of 1 Hz.
Pressing the Run button simulates a 10 second run where both the two conflicted control systems and a single unconflicted control systems are controlling the position of a cursor under exactly the same conditions (the same disturbance). The results of that run, which are produced nearly instantaneously after pressing Run, are shown in the upper right of the display.
The most important results are the ones in light red – labeled “Stability” – which are measures of how well the conflicted and unconflicted control systems controlled the cursor. The stability measure (S) is calculated as:
S = 1 - sqrt(Var(C)/[(Var(D)+Var(O)])
Var(C) is a measure of the observed variance of the cursor; Var(D)+Var(O) is a measure of the expected variance of the cursor – expected if there were no control. To the extent that there is control the observed variance of the cursor will be much smaller than its expected variance and the Stability measure, S, will be close to 1.0. When there is no control the observed variance of the cursor will be equal to its expected variance and the stability measure will be 0.0.
The display above shows the results of a run with the disturbance amplitude set to 1. In this case the Stability measure for the conflicted system – the Virtual Control Results – is 0.0 while that for the unconflicted control system – the True Control Results – is .994!! So the conflicted control system was not resisting this disturbance at all - it was not controlling – while the equivalent unconflicted control system was resisting teh disturbance quite well – it was controlling nearly perfectly. This is shown in the graph below the results. The grey line shows that the cursor that is “controlled” by the conflicted control systems moves exactly in synch with the 1 unit disturbance while the blue line shows that the effects of the distrubance on the cursor were considerably attenuated by the actions of the unconflicted control system.
What you are seeing here is a complete lack of control by the conflicted control systems when the amplitude of the disturbance is in the Dead Zone. You are also seeing that there is no Dead Zone for the unconflicted (actual) control system – it acts to resist the same disturbance and keep the cursor under control.
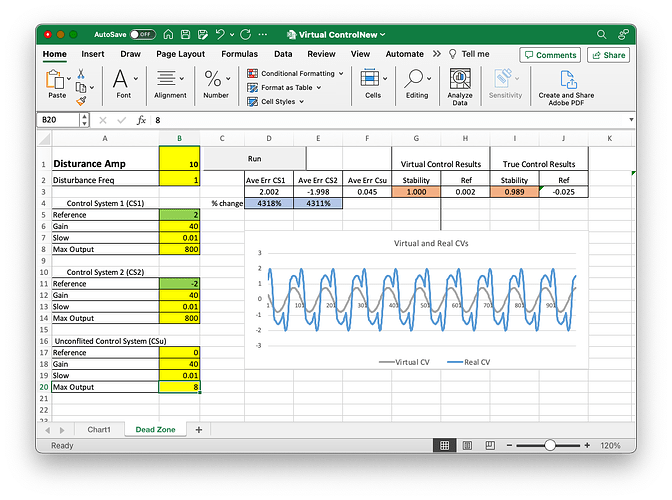
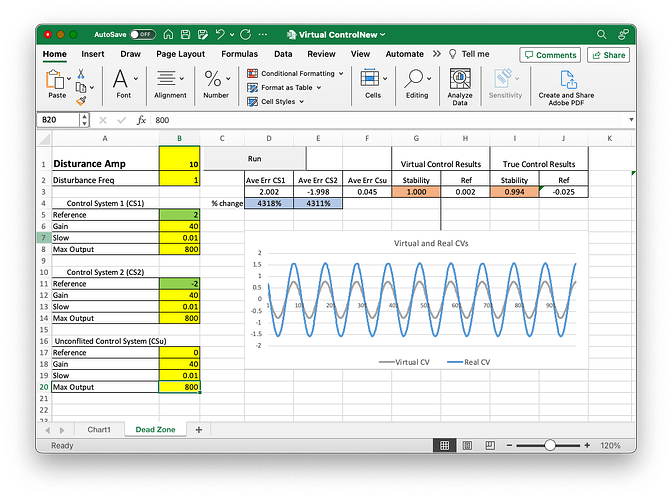
You can now use this spreadsheet to estimate the width of this Dead Zone by doing runs with varying values of disturbance amplitude and see which ones result in no control (Stability = 0.0) and which ones result in some amount of control (Stability>0.0). I’ve found that the Dead Zone for the conflicted systems of the strength entered into the spreadsheet (Gain = 40, Max Output = 8) seems to range from disturbance amplitudes of just over 0.0 to about 2 (0.0 amplitude can’t be used because it results in a denomintor of 0 for the stability calculation). Once the disturbance amplitude gets above two, the Stability measure becomes non-zero, as shown below, for a run when the disturbance amplitude is 3:
As you continue to increase the amplitude of the disturbance, the Stability measure for the conflicted control systems (the Virtual Control results) actually starts to increase; increased disturbance amplitude leads to better control! This is exactly the opposite of what happens with the unconflicted control system (the True Control results) where, as the amplitude of the disturbance increases, the Stability measure decreases; increased disturbance amplitude leads to worse control.
Thus, there are two ways to distinguish a virtually controlled variable – one controlled by conflicted systems – from a true controlled variable. A virtually controlled variable can be identified 1) by the existence of a Dead Zone where there is no resistance to disturbances with amplitudes in the Dead Zone range and 2) by the fact that increases in disturbance amplitude outside the Dead Zone range lead to increases in the ability to control the virtually controlled variable. For a true controlled variable there is 1) no Dead Zone and 2) increases in disturbance amplitude always lead to decreases in the ability to control a true controlled variable.
The above facts are true for a virtual controlled variable when the control systems "controlling’ it have equal Max Outputs. You can use the spreadsheet to see what happens when the Max Outputs of the two systems are unequal. I’ve done some explorations of what happens in this case but I’ll leave this for a separate post. For now, I developed this spreadsheet to see whether or not Bill Powers was right about the Dead Zone. And, once again, he was.