Equations of Control (was Re: Action and Behavior)

[MartinT]

[Martin Taylor 2013.06.30.17.03]

OK, Lloyd, here's an attempt to start what you are asking for. In

the following I’m trying to model a description targeted at someone
quite unaccustomed to the engineering approach to control, so please
will any grandmothers reading it please forgive my instructions on
egg-sucking technique (unless I have made some mistakes).

···

I’ve changed the subject line because this isn’t relevant to the
use of language in PCT, and because it could lead to a discussion
of how to approach teaching the engineering principles behind PCT.

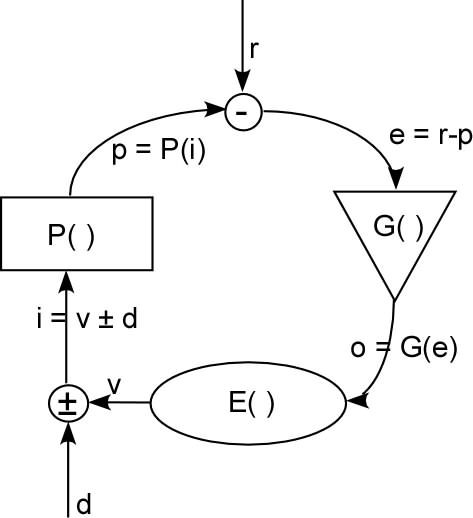
    [From Lloyd Klinedinst

(2013.06.30.1446)]

  The simple equations I have worked with from some early workshop

in PCT are: e = r - p and cv = a + d. Then I know something like
an equation needs to occur for cv to become i_q and
then get further transformed through the Input function to become
a p and get recycled. I look forward to CSGers confirming and
correcting these simple equations I have been working with. This
is why I would value PCT-standardized progressively simple to
complex sets of equations to express mathematically the scientific
core of PCT.

variables*.* *** we cannot ever write an equation that
relates the instantaneous values all around the loop at the same
moment in time.***
*** Any equation that takes account of the variation
in values of loop variables must also explicitly represent time.***
*** There are only two input variables to the loop ,“r”
and “d”,***

---

    One canno******t.***

[rsmarken]

[From Rick Marken (2013.07.02.0700)]

[Martin Taylor 2013.06.30.17.03]

MT: In the diagram, p = P(i), which means the effect of the Perceptual

Input Function operating on the input “i”. Typically, in simple
discussions of the control loop, P( ) is taken to just be a unity
multiplier, a straight-through connection. So let’s do that, and
say:

p = i.



p = i = v+-d   



Why the plus-minus? It is the difference between pursuit and

compensatory tracking.

RM: I don’t get this. First, where did v come from? If v and d are two environmental variables then how could either the sum or the difference be i? Aren’t v and d the inputs, i, and then, as tou say, p is a function if i so p = v + d or p = v-d. It’s the perceptions that differ, not the inputs. But actually I find that people seem to control the same perception in both compensatory and pursuit tracking: the difference between cursor and target position, c - t. The only difference is that in pursuit tracking t is variable; in compensatory tracking t is constant. Variatoins in t can are a disturbance to the controlled perception, c-t, in pursuit tracking; in compensatory tracking a variable disturbance is added to the subject’s output to produce c; so c = o + d in compensatory tracking. But the controlled perception is the the same in both cases. And as we’ve learned recently the controlled perception is actually not t - c but, rather the angle between t and c: arctan((t-c)/s).

Best

Rick

···

–
Richard S. Marken PhD
rsmarken@gmail.com
www.mindreadings.com

[MartinT]

[Martin Taylor 2013.07.02.10.56]

Here's the diagram again.

Does that answer your question?
Yes, you can think of it that way, but you can also think of it as
the diagram shows. I don’t think it makes any mathematical
difference. Where do you see the “cursor” in this diagram? If the perception
being controlled is “seeing the wife happy” and disturbances include
such things as a broken dish or the arrival of bad news, where is
“t”? The controller doesn’t oppose the breaking of the dish or
prevent the bad news from arriving, but acts so as to improve the
wife’s mood: v-d, compensatory tracking. The nearest thing I can see
for “t” is the reference value “wife perceived to be happy”.
Isn’t this true also of the classic on-screen following task? The
reference value for the cursor is that it be exactly on-target.
Where is the target? That’s a perception. By the action of
higher-level control systems it determines the reference value for
where the cursor should be, if the subject so chooses. So a more
correct way of diagramming pursuit tracking would not even have “d”
in the same loop. It would show up as a varying reference value.
That’s a complication I didn’t want in my “teach your grandmother to
suck eggs” level of explaining the steady-state equations. Using the
“plus-minus” approach is simpler and gives the same mathematical
result when the perceptual function is a unity multiplier.
The difference in the on-screen location-tracking task is that the
disturbance is added to the cursor in the compensatory task and to
the target in the pursuit task. That’s why the plus-minus in the
diagram.
We haven’t “learned” that yet. We may both believe it, but I’m still
working to try to demonstrate it. I decided to rewrite the whole
program to get rid of all the cruft that had adhered to it over
time, and last night the actual display and tracking component
worked.
In any case, how would it apply to any other tracking task? For
example, even in an on-screen task, how would it apply to keeping
one grey patch the same brightness as another? What would correspond
to the “angle” between the brightnesses?
Martin

···

[From Rick Marken (2013.07.02.0700)]

        [Martin Taylor

2013.06.30.17.03]

        MT: In the diagram, p = P(i), which means the effect of the

Perceptual Input Function operating on the input “i”.
Typically, in simple discussions of the control loop, P( )
is taken to just be a unity multiplier, a straight-through
connection. So let’s do that, and say:

        p = i.



        p = i = v+-d   



        Why the plus-minus? It is the difference between pursuit and

compensatory tracking.

  RM: I don't get this. First, where did v come from?

  But actually I find that people seem to control the

same perception in both compensatory and pursuit tracking: the
difference between cursor and target position, c - t.

  The only difference is that in pursuit tracking t is

variable; in compensatory tracking t is constant.

  Variatoins in t can are a disturbance to the

controlled perception, c-t, in pursuit tracking; in compensatory
tracking a variable disturbance is added to the subject’s output
to produce c; so c = o + d in compensatory tracking. But the
controlled perception is the the same in both cases. And as we’ve
learned recently the controlled perception is actually not t - c
but, rather the angle between t and c: arctan((t-c)/s).

[rsmarken]

[From Rick Marken (2013.07.02.0900)]

[Martin Taylor 2013.07.02.10.56]

[From Rick Marken (2013.07.02.0700)]

        [Martin Taylor

2013.06.30.17.03]

        MT: In the diagram, p = P(i), which means the effect of the

Perceptual Input Function operating on the input “i”.
Typically, in simple discussions of the control loop, P( )
is taken to just be a unity multiplier, a straight-through
connection. So let’s do that, and say:

        p = i.



        p = i = v+-d   



        Why the plus-minus? It is the difference between pursuit and

compensatory tracking.

  RM: I don't get this. First, where did v come from?

Here's the diagram again.



![loopFunctions7.jpg|473x518](upload://picaYS9iHfF5qyO3XTygEefdch6.jpeg)



Does that answer your question?

RM: Yes, the one about where v comes from. Thanks. the rest still makes no sense to me but, never mind. I haven’t got the time for this.

Best

Rick

···

  But actually I find that people seem to control the

same perception in both compensatory and pursuit tracking: the
difference between cursor and target position, c - t.

Yes, you can think of it that way, but you can also think of it as

the diagram shows. I don’t think it makes any mathematical
difference.

Where do you see the "cursor" in this diagram? If the perception

being controlled is “seeing the wife happy” and disturbances include
such things as a broken dish or the arrival of bad news, where is
“t”? The controller doesn’t oppose the breaking of the dish or
prevent the bad news from arriving, but acts so as to improve the
wife’s mood: v-d, compensatory tracking. The nearest thing I can see
for “t” is the reference value “wife perceived to be happy”.

Isn't this true also of the classic on-screen following task? The

reference value for the cursor is that it be exactly on-target.
Where is the target? That’s a perception. By the action of
higher-level control systems it determines the reference value for
where the cursor should be, if the subject so chooses. So a more
correct way of diagramming pursuit tracking would not even have “d”
in the same loop. It would show up as a varying reference value.
That’s a complication I didn’t want in my “teach your grandmother to
suck eggs” level of explaining the steady-state equations. Using the
“plus-minus” approach is simpler and gives the same mathematical
result when the perceptual function is a unity multiplier.

  The only difference is that in pursuit tracking t is

variable; in compensatory tracking t is constant.

The difference in the on-screen location-tracking task is that the

disturbance is added to the cursor in the compensatory task and to
the target in the pursuit task. That’s why the plus-minus in the
diagram.

  Variatoins in t can are a disturbance to the

controlled perception, c-t, in pursuit tracking; in compensatory
tracking a variable disturbance is added to the subject’s output
to produce c; so c = o + d in compensatory tracking. But the
controlled perception is the the same in both cases. And as we’ve
learned recently the controlled perception is actually not t - c
but, rather the angle between t and c: arctan((t-c)/s).

We haven't "learned" that yet. We may both believe it, but I'm still

working to try to demonstrate it. I decided to rewrite the whole
program to get rid of all the cruft that had adhered to it over
time, and last night the actual display and tracking component
worked.

In any case, how would it apply to any other tracking task? For

example, even in an on-screen task, how would it apply to keeping
one grey patch the same brightness as another? What would correspond
to the “angle” between the brightnesses?

Martin

–
Richard S. Marken PhD
rsmarken@gmail.com
www.mindreadings.com