Feedforward, feedback, and pure open loop

[BRUCE_STEPHANIE_ABBO]

[From Bruce Abbott
(2009.12.25. 1615 EST)]

Here’s a set of
diagrams that appear on Wikipedia distinguishing between pure open loop (“feednowhere”),
feedforward, and feedback systems, as defined in engineering:

Note that, in these systems,
the “input” is what we in PCT would call the reference signal and
the output is what we would call the input.

In the top (open loop)
diagram, the input might be the setting on a rheostat, which “controls”
the speed of a motor. (Motor speed is the output). A disturbance such as a load
on the motor will cause the motor speed to change from its speed setting and
this open loop system will do nothing about that. The motor will just slow to a
new equilibrium determined by the power setting and the load.

In the middle (feedforward)
system, there is an added component that senses the disturbance and passes its
value to a comparator (the circle with the “x” in it), where it is
subtracted (after suitable scaling) from the input. (Remember, the “input”
is equivalent to PCT’s reference.) The system is still open loop (there
is no feedback). Feedforward is scaled so as to take account of the known
effect of the disturbance on the output; if done correctly, the changing input
(reference) will be exactly sufficient to offset the effect of the disturbance.
For example, one might work out exactly by how much the motor slows under
various loads; the feedforward system would measure the load and change the
rheostat setting so as to boost the power exactly the right amount to
compensate for the load.

This system would be most
beneficial if you were dealing with a sluggish system and the disturbance could
be sensed enough in advance of its effect on the output to overcome the
sluggishness. (The effect of the disturbance on the output would also have to
be stable over time.)That is, the system would begin responding to the
disturbance before it arrived, giving time for the slow response to build up so
that it takes effect in time to prevent much change in the output. I’m
old enough to remember the Granatelli Indy turbine car that almost won the Indy
500 in 1967. The gas turbine engine, which had been designed for use in
helicopters, responded sluggishly to throttle changes. Parnelli Jones,
the driver of the car, stated that he had to learn to get off the accelerator
well ahead of each turn and then mash it down as he entered the turn –
something you definitely don’t want to do when driving a
piston-engine car! But the turbine’s lag was so great that it would only
begin to accelerate again as the car came out of the turn. Jones was not
actually behaving strictly as a feedforward system (as defined in the second
diagram), but one can see in this example the benefit of advancing the changes
in the reference signal when the system changes its output only after a
considerable delay. Although not “feedforward” according to this
strict engineering definition, it’s easy to see how the term might
actually be applied more generally, to any system that uses prediction as part
of its basis of action.

The bottom diagram shows the
usual negative feedback control system. The feedback is provided by a sensor
that determines the current state of the controlled variable (the output) and
subtracts this from the input. The resulting error signal causes actions that
oppose the effect of the disturbance. A “feedback regulated” motor
controller would have a sensor for motor speed. The input speed setting would
be compared to the actual motor speed as given by the sensor and the difference
between them would be used to generate changes in motor torque as needed to
compensate for changes in the load.

Bruce

[Bill_Powers1]

[From Bill Powers (2009.12.25.1830 MDT)]

Bruce Abbott (2009.12.25. 1615 EST) –

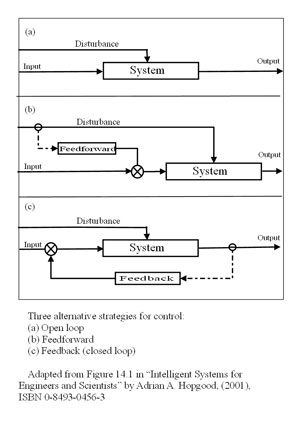
BA: Here’s a set of diagrams that appear on Wikipedia distinguishing
between pure open loop (“feednowhere”), feedforward, and feedback
systems, as defined in engineering:

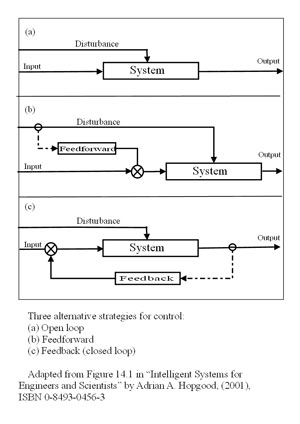
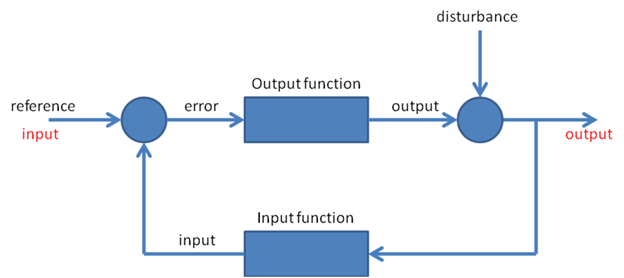
Note that, in these systems, the “input” is what we in PCT would call the
reference signal and the output is what we would call the input.

In the top (open loop) diagram, the input might be the setting on a
rheostat, which “controls” the speed of a motor. (Motor speed is the
output). A disturbance such as a load on the motor will cause the motor
speed to change from its speed setting and this open loop system will do
nothing about that. The motor will just slow to a new equilibrium
determined by the power setting and the load.

In the middle (feedforward) system, there is an added component that
senses the disturbance and passes its value to a comparator (the circle
with the “x” in it), where it is subtracted (after suitable scaling) from
the input. (Remember, the “input” is equivalent to PCT’s reference.) The
system is still open loop (there is no feedback). Feedforward is scaled
so as to take account of the known effect of the disturbance on the
output; if done correctly, the changing input (reference) will be exactly
sufficient to offset the effect of the disturbance. For example, one
might work out exactly by how much the motor slows under various loads;
the feedforward system would measure the load and change the rheostat
setting so as to boost the power exactly the right amount to compensate
for the load.

BP: This is a qualitative argument, as well as being circular. Of course
if you do the scaling “correctly” for offsetting the effect of
the disturbance, the effect of the changing reference “will be
exactly sufficient to offset the effect of the disturbance.” That is
what “correctly” means. But if you do it incorrectly, which is
almost inevitable when you try to accomplish this with a real system, the
sufficiency comes into doubt.

Adding to the input a signal indicating the size and direction of a
disturbance is not enough to counteract the effect of the disturbance on
the output. As in Cooper’s diagram, you need a computer in the link to
calculate the size of the effect of the disturbance on the output via the
system that is disturbed. You need to take into account the intervening
properties of the System, the system’s effect on the motor, and the
motor’s response given the current load. It is highly unlikely that in
any real system these computations can be reduced to a simple adjustment
of a constant of proportionality.

In a true feedback control system, the nonlinearity of the intervening
System, and disturbances both anticipated and unanticipated, do not have
to be known in advance. If the controller is stable, all that matters is
the loop gain and the accuracy of sensing the controlled output. The
output (CV) will have the magnitude set by the input (reference signal)
as accurately as the output can be sensed.

This system would be most
beneficial if you were dealing with a sluggish system and the disturbance
could be sensed enough in advance of its effect on the output to overcome
the sluggishness. (The effect of the disturbance on the output would also
have to be stable over time.) That is, the system would begin responding
to the disturbance before it arrived, giving time for the slow response
to build up so that it takes effect in time to prevent much change in the
output.

How would you adjust this system to have just the right effect? You would
have to operate it and see what the result was. If the result wasn’t
right, you would make an adjustment of gain, linearity, and lag to make
the result closer to the desired one. As you continued to use this
system, you would have to continue monitoring its performance, comparing
the performance with what was desired, and making further adjustments.
But it wouldn’t matter if the performance kept changing unpredictably
with time and rough usage; you could keep the performance close to the
desired level because this system would just be part of the feedback
function between your adjustments and the sensed performance. The
accuracy of control of performance would be determined by the accuracy of
sensing, not the accuracy of the processes connecting input to
output.

I’m old enough to remember the
Granatelli Indy turbine car that almost won the Indy 500 in 1967. The gas
turbine engine, which had been designed for use in helicopters,
responded sluggishly to throttle changes. Parnelli Jones, the driver of
the car, stated that he had to learn to get off the accelerator well
ahead of each turn and then mash it down as he entered the turn –
something you definitely don’t want to do when driving a
piston-engine car!

Right. Parnelli Jones was the negative feedback control system I am
talking about. He adjusted the way he produced output (timing and amount)
until the sluggish response was happening the way he wanted it to happen.
This required changing the relationship between the time of changing the
throttle setting and the desired time for the response to occur, and of
course between the amount of change of throttle setting and the amount of
response. This was not a set-it-and-forget-it adjustment; it went on
continuously, being affected, I would expect, by the changing weight of
the car, the condition of the tires, and the condition of the track
surface. The adjustment was done by negative feedback control of the
perceived result.

But the turbine’s lag was
so great that it would only begin to accelerate again as the car came
out of the turn. Jones was not actually behaving strictly as a
feedforward system (as defined in the second diagram), but one can see in
this example the benefit of advancing the changes in the reference signal
when the system changes its output only after a considerable delay.
Although not “feedforward” according to this strict engineering
definition, it’s easy to see how the term might actually be applied more
generally, to any system that uses prediction as part of its basis of
action.

And incorrectly, as I see it. I have given my reasoning in previous posts
today. What’s wrong with it?

The bottom diagram shows the
usual negative feedback control system. The feedback is provided by a
sensor that determines the current state of the controlled variable (the
output) and subtracts this from the input. The resulting error signal
causes actions that oppose the effect of the disturbance. A “feedback
regulated” motor controller would have a sensor for motor speed. The
input speed setting would be compared to the actual motor speed as given
by the sensor and the difference between them would be used to generate
changes in motor torque as needed to compensate for changes in the
load.

If you used a two-level controller as in chapter 5 of LCS3, you would
find that the changes in throttle setting would increase by a large
amount when the reference-speed was changed, far more than needed for the
actual speed change. This would greatly reduce the apparent lag in
response of the engine, and it would be safe because the lower-order rate
control would quickly reduce the setting as the speed approached the new
reference setting. A driver might be able to learn to do this, though an
automatic controller could probably react faster.

The main thing being overlooked here is that negative feedback control is
based on long-term perceptions as well as short-term ones. When a driver
pulls into the pit area for a steering adjustment, it’s not because he
noticed a little pull or understeer on the previous turn. It’s because he
has been noticing this effect on enough turns to be sure it’s happening.
The adjustment is made not all at once, but in steps, because
overadjusting is as bad as underadjusting. It’s a control process
happening over many repetitions of some behavior, not just one.

It’s time, as Gary Cziko put it, to “put a model where one’s mouth
is.”

Best,

Bill P.

[_Boris_Hartman]

Hi Bruce !

BA : Note that, in these systems, the �input� is what we in PCT would call
the reference signal and the output is what we would call the input.

BH : If I understand right there are 3 inputs :
1. Input as reference
2. Disturbance as input
3. Output as input

Please take into account that maybe I misunderstood something.

Best,

Boris

[BRUCE_STEPHANIE_ABBO]

Hi Boris,

BA : Note that, in these systems, the “input”
is what we in PCT would call

the reference signal and the output is what we would call
the input.

BH : If I understand right there are 3 inputs :

1. Input as reference

2. Disturbance as input

3. Output as input

That’s right. But the terms “input” and
“output” can be confusing when comparing their use in engineering
and in the standard PCT diagram.

Here is the PCT-style control system diagram with components
repositioned as normally shown in engineering diagrams. The red text indicates
labels used in the engineering diagram. This arrangement emphasizes the fact
that in engineering, the “input” is a control that an operator
could manipulate and the output is the variable whose value the operator would
be setting. For example, in a 5V regulator such as is found in computers and
other electronic devices, the input is the voltage that the designer wants the
regulator to produce and the output is the actual voltage produced. Because of
negative feedback (and especially if loop gain is high), the difference between
the desired and actual voltages will be small, and disturbances caused by various
electrical loads will be almost completely compensated for within the limits of
the system to do so.

The output (in red) is in this case the regulated voltage
and is used elsewhere to power the electronics. It is in this sense that the
regulated voltage is the output of the device. In the diagram, inputs and
outputs (in red) are external to the regulator. The disturbance is also
external to the regulator and thus, you are correct, it is also effectively an
input to the device.

It is also possible to define inputs and outputs to or from
components within the regulator. That’s how those terms are being
used in the PCT diagram. The input in the PCT diagram is the signal
representing the sensed state of the controlled variable, which serves as one
input to the comparator (the left circle in the diagram). The reference is the
second input to the comparator, and the effort signal is the comparator’s
output, which is transformed by the output function into a variable that can
oppose the effect of the disturbance on the controlled variable (the circle on the
right). That variable is the one labeled “output” in the PCT
diagram. The controlled variable has two inputs: the output from the output
function and the disturbance. The difference between them is the value of the
controlled variable, which is sensed by the input function.

If we consider the control system to be a single device, it
has two inputs (reference and disturbance) and one output: the controlled
variable. If we are looking at the individual components, then each component has
its own input or inputs and output. In the PCT diagram, what is labeled as “input”
is the perceived value of the controlled variable and is internal to the
control system, not something coming from outside of it. It is an input only to
the comparator.

Best wishes,

Bruce

[MartinT]

[Martin Taylor 2009.12.27.12.00]

Hi Bruce !
BA : Note that, in these systems, the “input” is what we in PCT would call
the reference signal and the output is what we would call the input.
BH : If I understand right there are 3 inputs :
1. Input as reference
2. Disturbance as input
3. Output as input
Please take into account that maybe I misunderstood something.

What you understand to be “input” depends on what you consider to be
“inside” and what you consider to be “outside”. Any signal (an effect
on a variable) that goes from “outside” to “inside” is an “input”.

For the canonical PCT control loop: there
are two inputs: R and D. The “output” (O) is a signal within the loop,
not an input to the loop.

However, if you are talking about input to the person from the
environment of the person, then there is only one input, S, which is a
combination of O and D, neither of which is independently an input to
the person from the environment. If you are talking about input to the
loop from its environment (which includes whatever in the person
provides the reference value) both R and S are inputs.

In the diagrams that Bruce presented, there are two inputs, “input” (=
PCT “reference”) and “disturbance”.

What you understand to be “input” depends on what you consider to be
“inside” and what you consider to be “outside”. Any signal (an effect
on a variable) that goes from “outside” to “inside” is an “input”. In
case of possible ambiguity, you should specify input to what from what.

Martin

[BRUCE_STEPHANIE_ABBO]

[From Bruce Abbott (2009.12.28.0830
EST)]

In my previous message,
replying to Boris Hartman, I presented a diagram of a control system with
components reoriented to resemble the way engineers typically present them.
After posting the diagram I spotted a minor error: the word “input”
(in black) that labels the arrow entering the comparator should have labeled
the arrow entering the input function box. In PCT, the arrow from input
function to comparator is of course called the perception. It is, however, an
input to the comparator.

If I made any other errors, I’m
sure that someone will point them out!

Bruce