Flip-flop

[MartinT]

[Martin Taylor 2017.12.20.13.29]

[From Rupert Young (2017.12.20 18.15)]

(Martin Taylor 2017.12.19.12.01]

[From Rupert Young (2017.12.19 16.05)]

      (Martin Taylor 2017.11.23.11.30]

        Here's a spreadsheet that implements a

two-way flip-flop. It’s not very elegant, and it may be
buggy, but it seems to work. I expect you could easily
improve on it in various ways, or make a one-way one (i.e.
with values never below zero).

      This appears to show a B output of > 1 even though B input

is zero. In that case shouldn’t B output always be zero?

    No. You have two inputs into each perceiver, the input from

below (which I call the “input”) and the feedback input from the
other output. So long as the feedback input is strong enough, it
doesn’t matter what the input from below does, the flip-flop
will maintain the same output high and the other zero. If Aout
has been high, it will stay high until Bin-Ain>some
threshold. At least that’s what it is supposed to do, if my
spreadsheet programming is correct, which is far from
guaranteed.

  Well, it seems strange that even though Bin is zero this would

provide a category of B. Are you sure that is what it is supposed
to do?

It is exactly what a flip-flop is supposed to do. I explained in my

previous message why the simple flip-flop is unlikely to be what you
want as a category recognizer. It is a category discriminator,
without a third “none-of-the-above” output. In words, it is 100%
certain that either A or B is true but not both, and the question is
which one it is. If Bout is positive when Bin is zero, that is
because Bin is greater than Ain, or if at this moment it is not, it
has been up to now and the excess of Ain is as yet insufficient to
say that things have changed.

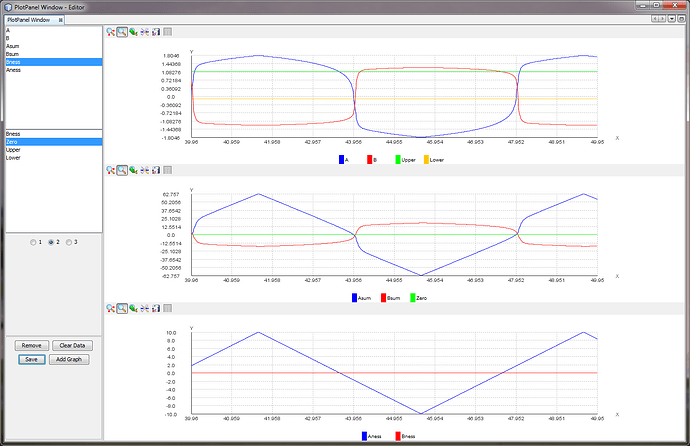
  Here's my replication of your spreadsheet model. Initially B is

suppressed such that it is -ve. Initially A is +ve, but when it
goes -ve it then increases Bsum due to the -ve weight. Perhaps
Bsum should not go above zero if Bin is zero?

No. That is exactly what it is supposed to do.

      How does this work if B input is not

zero, and has a different phase to A, and sometimes A=B? For
the latter shouldn’t only one output be non-zero?

    Yes, except for the transition period while the flip is

flopping. When A=B, whichever one was previously high stays high
until the imbalance of the inputs is sufficient to overwhelm the
cross-feedback loop effect, Then you have several samples of a
transient condition (in the analogue system that could be
pico-seconds, seconds, minutes, or years) while both are
non-zero until the flop is complete. In the spreadsheet, I used
a leaky integrator to smooth the transient. Without looking back
at the spreadsheet, I forget the leak rate, but it had to have a
time-constant of several samples.

  That's not what I am finding here. B has the same value as A,

albeit briefly.

Your diagrams show that it is what you find in your replication,

exactly what I said. During the transition period, both are briefly
positive, and there has to be a moment when both have the same
positive value.

  ![njnmaeeoekkpfmok.png|1392x900](upload://zM3CYMhTFbqdlZo5NyTK3PluqY9.png)





  In practice the model doesn't appear to be as straightforward as

the theory would seem to suggest,

Well, so far, it seems to be working in a very straightforward

manner as the theory says it should. What problem do you still see?

Do you want me to produce a polyflop demo instead? I was going to do

that, but I have to figure out how to program something like
subroutines in Excel so I don’t have to deal with thousands of lines
of the data for each sample moment and can simply produce graphs for
the inputs and outputs. Probably Excel isn’t the best language to
use, but I just wanted to show something quick and dirty that works
as intended. I can’t spend much time on programming a polyflop, as I
am spending most my time on PPC. A proper polyflop simulation
probably needs a parallel programming structure anyway, and that’s a
bit beyond me. Maybe a randomized order of updating per sample would
do. I don’t know, but it could be worth a try.

  so I don't think I can spare any more time on this myself.

However, if you are able to revisit the model I’d be very
interested to see that it can work.

You have that now. I suspect that the problem is that you were

looking for a circuit that is supposed to do something different.
You want to suppress the category output if there’s no analogue
variable to be categorized. If the flip-flop discriminates between
“Lion” and “Tiger” you want it to be inhibited if the analogue
perception of both are less than some threshold. It shouldn’t be too
hard to add an inhibitory connection based on the sum of Ain and
Bin. You might want to do that in a practical robot, but it’s simple
enough that I don’t think it’s worth doing as an addition to this
working simulation. However, as always I may change my mind
tomorrow.

Martin

···

  Rupert