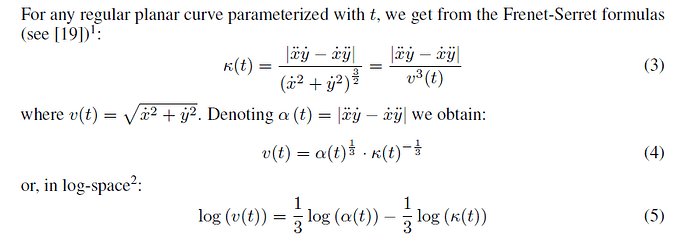[From Rick Marken (2018.08.17.06:00)]
[From Bruce Abbott (2018.08.16.0930 EDT)]
Â
[Rick Marken 2018-08-15_18:27:22]
 [From Bruce Abbott (2018.08.15.1030 EDT)]
Â
BA: Pollick and Shapiro (1995) performed an analysis of the velocity-based formula… Their analysis was essentially identical to yours (both add affine velocity to the regression equation as a separate factor) but their conclusion was not. …Â they concluded that the power coefficient of 2/3 will appear across observations only if the affine velocity is constant across observations…
RM: Maoz et al. (2006) also found what we had found and came to the same mistaken conclusion about what it meant as did Pollick and Shapiro (1995). We addressed this in our rebuttal:" [their conclusion]** amounts to assuming that one’s theory of the cause of the power law is correct and any deviation of data from the theory is the fault of the data. **
Â
BA: The fact that you just restated this misconception is proof that you either did not read, did not understand, or have chosen to ignore, the analysis I presented that should be the subject of your reply. That analysis is a refutation of the position you take above in the second bolded section.
RM: I don’t understand what there is to refute. Both Pollick and Shapiro (1995) and Maoz et al. (2006) found exactly what we did: that the degree of deviation of the power coefficient found by regressing curvature on velocity will deviate from the power law value  (1/3 or 2/3 depending on how the variables are measured) in proportion to the covariance between curvature and the omitted variable, affine velocity. The deviation from 1/3 or 2/3 will be zero when the covariance between curvature and velocity is zero, which will happen when affine velocity is constant throughout the trajectory.Â
RM: Maybe you think that “only if the affine velocity is constant across observations…” means something different than what I think it means. I think it means “constant across observations throughout a trajectory”. Maybe you think it means “constant across observations of different trajectories”. Is that it? If so, that is not what Pollick and Shapiro (1995),  Maoz et al. (2006) and Marken & Shaffer (2018) mean by constant affine velocity.
Â
RM: But ignoring the mathematics for now, I’m still interested in knowing what you think is the correct application of PCT to the power law…
Â
BA: Ignoring the mathematics? Let’s not try to duck the issue by changing the subject. At this point there are only two appropriate responses to the analysis I laid out: (1) admit that you have made a serious error of mathematical logic, or (2), provide a mathematical proof that invalidates my refutation. To be clear, the serious error to which I refer is the following: That the formula for curvature implies that for a time series of V,C pairs, “the true (mathematical) power coefficient (beta) relating these variables is 2/3.�
Here’ the proof that the true power coefficient (beta) relating V (called v(t) and C (which is here measured as k(t), which is proportional to the reciprocal of the Gribble Ostry equatoin for curvature measure as R) is -1/3 (from Maoz et al. ,2006).Â
And their version of the omitted variable analysis is:Â
RM: The last sentence basically confirms our conclusion: that any trajectory, regardless of how it is produced, where log (affine velocity) and log (curvature) are uncorrelated, will precisely correspond to the power law.Â
Â
BA: To get you started along this path, the first thing I need from you is evidence that you have read the argument against your conclusion and have understood it well enough to restate it correctly in your own words. In your reply, insert restatement here:
RM: I’m sure that I can’t provide such evidence even if I do. I think we’ve reached the point where this is getting us nowhere. My goal in this whole long debate was simply to try to get people to ignore the power law and do some PCT research – research aimed at testing to determine what perceptual variable people control wen they move. I think it’s pretty clear that no one wants to do this; they want to study the power law. So go ahead. Do the research, publish it and I’ll see what I think. Maybe you are all geniuses and I’m just a self- deluded moron. That will be OK. I’m still pretty rich and very good looking. So I’ll get by;-)
BestÂ
Rick
···
–
Richard S. MarkenÂ
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
                --Antoine de Saint-Exupery