Sorry Martin and Fred ![]()
···
From: Richard Marken (rsmarken@gmail.com via csgnet Mailing List) csgnet@lists.illinois.edu
Sent: Sunday, May 13, 2018 9:47 PM
To: csgnet@lists.illinois.edu
Subject: Re: On “variables” (was Re: Do we control “environmental variables”?)
[Rick Marken 2018-05-13_12:46:46]
[Martin Taylor 2018.05.12.23.38]
[From Fred Nickols (2018.05.11.0709 ET)]
FN: Rick: Your paragraph below leaves me completely confused. First you say “It is not environmental variables that are controlled but aspects(functions) of those variables that are controlled.� Then you say, “The aspects of the environment that are controlled are called controlled variables.� Which is it - aspects of variables or aspects of the environment? More important, please provide an example that illustrates the distinction you are trying to make.
MT: I’m not surprise he leaves you completely confused. “It is not environmental variables that are controlled, but aspects [functions] of those variables that are…called controlled variables” indeed! I don’t know what Rick is calling a “variable” these days, but for some unfathomable reason he has a long history of insisting that the result of a function of several variables is not itself a variable.
RM: Actually, I have never insisted that. In all of my research the aspects (functions) of environment variables that I have shown to be controlled are, of course, variables themselves. This fact is even clear from the little segment of my post that you quote: “It is not environmental variables that are controlled, but aspects [functions] of those variables that are…called controlled variables”. In other words functions of several environmental variables are themselves variables – controlled variables. You really don’t have to lie about me in order to get your misconceptions about PCT out there.
HB : If anybody have misconceptions about PCT out there is you Rick. You don’t understand PCT, you manipulate with PCT. It is probably everything what you probably do in your everyday life to achieve your goals. As Bill wrote, that people will do anything that they has to do, to achieve their goals. And that’s exactly what you are doing when you manipulate with PCT.
Boris
Best
Rick
The rest of us, I think, can safely use “variable” and “function” as does the rest of the world, which is rather less complicated. A “variable” is something that can change its value or magnitude, and can be represented by a number, (a “scalar variable”), an ordered set of numbers called a “vector” that has scalar numbers (or possibly other vectors) as its elements, or a label or an ordered set of labels (a vector that has labels as elements). Variables do not have “aspects”, though vectors do have “elements” that might in non-technical discourse be thought of as “aspects”. Each scalar number (or sub-vector) in a vector is an element of the vector. A “function” performs some manipulation on an input variable and produces another variable as its output or, in casual language, its product. Both input and output can be any of the three kinds of variable or a mixture of them.
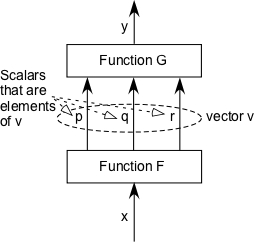
The Figure illustrates two functions, labelled “F” and “G”. Function F has a scalar input and a vector v as its output. Vector v has three scalar elements (p, q, r) . Function G has a vector of three scalars as input and a single scalar as output. We can write these as v = F(x) or {p, q, r} = F(x), and y = G(v) or y = G(p,q,r). Finally we can write y = F(G(x)), or we could define a function H(.) = G(F(.)), where the dot indicates an uncommitted variable.
In PCT, at least below the category level, the inputs of perceptual functions are always vectors (an ordered set of scalars) and the output is always a scalar number (of, say, neural firings per second), like Function G in the Figure. Scalar numbers do not have “aspects”. They just are what they are. In the case of perceptual functions, it may be that all the inputs derive ultimately from sensory data, some from imagination and some from sensory data, or all from imagination. If they are all from sensory data, then the perceptual function can determine an inverse function (like Function F in the figure) that converts x into the vector v = {p. q. r}. If the inverse is exact, then the equivalent of function H(.) = G(F(.)) is a unity transform and y = x. But The inverse need not be exact. For example H(.) may approximate log(.), as is usually (outside PCT, but sometimes within PCT) assumed to be the case. Always, however, if x is a function of time x = x(t), there is always a delay, so that y(t) = H(t-delta_t), and x ≠y except by momentary coincidence.
Properties of the environment may have labels such as height, aboveness, greenness, pressure, which are irrelevant when considering control, which is concerned with “how much” height (weight, temperature, speed, hardness, bigger-than, …), the property has, not with the label. All of those “how much” questions have scalar variables as answers, which could be the values of variables in a control loop.
“What is it” enters into control only because certain properties tend to go together often enough and usefully enough to have been reorganized into perceptual functions over either evolutionary time or the time of an individual’s life. Perceptual functions that do not have a corresponding property in the environment are likely to vanish during reorganization or diminished evolutionary fitness of the organism that bothers to control them.
Perceptual functions that do correspond to something real in the environment that is worth controlling are more likely than those that don’t to survive evolutionary or reorganizational stresses (I guess that statement approaches tautology :-). A transient perceptual function may not have the environmental equivalent of a function G, though it may determine one, but it can still be controlled through the real environment by influencing p, q, and r independently, as though a real x were being influenced. If the environmental “x” really exists, then influencing it is more efficient than influencing p, q, and r independently in the proper relationship. To make this more concrete, imagine the difference between getting six people to move a table, one on each leg and two at opposite sides holding the top. Now imagine those same six people trying to mime the actions of moving the table without having an actual table to move. Which is easier?
Solid objects then have a set of numbers that could be labelled height, width, depth, weight, redness, blueness, greenness, among other. These labels might be called “aspects”, but to PCT they are just the representation of the ordering of the elements of a vector of numbers, each of which, if it corresponds to a perceptual variable, may be a scalar variable in its own control loop. The scalar variables that correspond to x and y in the Figure are all that counts in any one loop, because the Powers version of PCT does not allow for vector variables as perceptions, or anywhere else that is usually represented by a single line in a diagram.
The above Figure can be recursively developed, because p, q, and r might each be a vector, and be split out into its separate components and later recombined by functions analogous to F and G. This kind of recursion can be carried forward indefinitely, but each of those levels of splitting and recombining can be subsumed in the analogue of function H.
I hope this helps clarify the relation between variables and functions. A function has one or more variables as inputs and one or more variables as outputs. Below the category level, perceptual functions have vectors as inputs and scalars as outputs, while the environmental functions they determine have scalars as inputs and vectors as outputs.
Martin
–
Richard S. Marken
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
–Antoine de Saint-Exupery