[From Rick Marken (2015.02.10.1120)]

···
Bruce Abbott (2015.02.09.1750)
RM: But I’ll correct it here. What I meant to say was:
RM: All that’s very interesting but what I have shown is that the disturbance to the mass in a mass spring system IS COMPLETELY EFFECTIVE, so for all intents and purposes, the gain of this negative feedback system is 0.
BA: Well, perhaps I didn’t read carefully enough, but that’s exactly what I TOOK you to be saying.
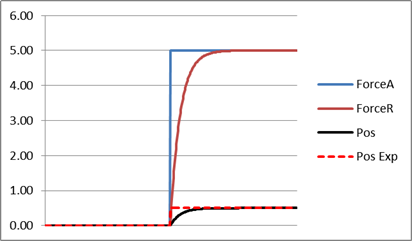
RM: OK, I re-read your story and it seems that you did understand that I said that there is no disturbance resistance in a mass spring system. The restoring force that is “generated” by the “disturbance” is just the reaction force of Newton’s third law: action - reaction. The action is the force, Fa, that you apply to the mass to displace it (what you call the “disturbance”); the reaction is the restoring force, Fr, that, according to the third law, is equal and opposite to the applied force: Fa = - Fr.
RM: So if the restoring force, Fr, in a mass-spring system is the disturbance resistance of a negative feedback system then so is the reaction force that exists when a force is applied to any mass. When you push on a large block of lead, for example, the block produces a reaction force, Fr, that is equal and opposite to your applied force, Fa. Because all matter is somewhat elastic, the force you apply to the block displaces its surface just as the force you apply to a mass on a spring displaces the spring. However, the spring constant of the block is very large so the displacement produced by the applied force is infinitesimally small. That is, by Hooke’s law, the displacement, x, produced by Fa is x = 1/k*Fa. Clearly, if k is close to being infinitely large, x will be close to being infinitesimally small. But the displacement, x, exists so when you stop pushing on the block of lead the reaction force, Fr, “restores” the surface to its original position.
BA: You can see this illustrated in my little dialog, where Obi Wan explains to Luke an implication of the disturbance being completely effective (i.e., no resistance being developed to it whatsoever): coffee cups falling through the table and non-supportive floors.
RM: Apparently Obi Wan didn’t know about Newton’s third law.
BA: So, the rest of my post is relevant and shouldn’t be ignored on the basis of irrelevance. My bottom line: your conclusion is total nonsense, for all the reasons I’ve already given.
RM: And I think Obi Wan’s conclusion is nonsense for the reasons I just gave. If he considers the reaction force that keeps a coffee cup from going through the table to be an example of disturbance resistance then he really needs some tutoring in basic physics.
RM: But the real problem with the “equilibrium theory” approach isn’t that it mistakes Newton’s third law for disturbance resistance. The real problem is that it is trying to account for control – purposeful behavior – using causal models. This game was finally given away when you posted this closed-loop model of a mass-spring system:
RM: This diagram shows that you consider an equilibrium system to be a purposeful system – a control system – as indicated by your inclusion of a reference position in the model. What this model says is that you consider the mass spring system to have a purpose; its purpose is to have the mass to be at the resting position. This is simply animism – attributing purpose to purposeless systems – disguised with some fancy math and terminology.
RM: My simulations demonstrated that this model of a mass spring system is incorrect, and that it is incorrect because of the inclusion of the reference. But anyone should have been able to tell that just from looking at the diagram. This is a diagram of a system that has a purpose (goal) – the reference for the position of the mass. Even without knowing PCT I think we can all agree that masses on springs are not purposeful systems. And it is also clear that even though you can legitimately call them negative feedback systems (as per my earlier post) they don’t resist disturbances. All they do is react (per Newton’s Third law), a fact that is easily demonstrated by simply pushing the mass to a new position and noting that you can hold it in that “disturbed” position and the system does nothing about; it just produces a reaction force equal and opposite to your applied force (the 3rd law). The mass spring system doesn’t compensate for disturbances because it doesn’t care what happens to the position of the mass; it doesn’t want the mass to be in the resting state.
RM: The problem with this 'equilibrium theory" game of using non-purposeful systems, like the mass spring system, as examples of systems that can produce purposeful behavior, beside the fact that it is completely wrong, is that it gives ammunition to those who, as Bill used to say, have an allergic reaction to the concept purpose in behavior and, therefore, argue that PCT is not needed to explain (purposeful) behaviors, such as limb movements. Therefore, I have no idea why Bruce and Martin are so enamored of equilibrium theory. I would really like to hear what they think “equilibrium theory” has to contribute to PCT. As far as I can see, all it has to contribute is confusion.
RM: PCT is about the fact that purposeful behavior is the control of perception. Understanding purposeful behavior, then, is a matter of understanding what perceptions organisms are controlling and how they control them. This was Bill’s incredibly important contribution to our understanding of the nature of living systems. I don’t see how the study of equilibrium systems – which neither perceive nor control – fits into this vision.
Best
Rick
–
Richard S. Marken, Ph.D.
Author of Doing Research on Purpose.
Now available from Amazon or Barnes & Noble