[From Rick Marken (2010.05.22.1430)]
Martin Taylor (2010.05.21.23.17) --
Rick Marken (2010.05.19.2300)--
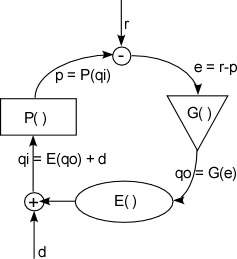
Bill's derivations are on pp. 145-146 of LCS I; for the closed-loop case he
gets (using your notation):�qo = 1/E (r - d)
This makes no sense, since in most analyses that are shown on CSGnet, E() is
the identity function, which would giveqo = 1/(r-d)
You must be thinking of E(), then, as the function relating the
disturbance to the controlled variable. I thought that you had been
equating E() to the feedback function. In terms of the equation on p.
139 in LCS I, which says:
qi = g(qo)+h(qd)
I assumed that, in our current notation, this maps to
qi = E(qo) + d
with h() as the identity operator transforming the disturbance
variable into qi. The behavioral illusion is then the appearance that
an observed relationship between qo and d reflects the system
function,
qo = F(d)
rather than the feedback function, as in
qo= 1/E(r-d)
The question is whether one who observes an S-R relationship (the
�relationship between d and qo) will conclude that this relationship reflects
�F(), the organism function, or 1/E(), the inverse of the feedback function.
�Obviously, conventional researchers take an observed relationship between d
�and qo to be a reflection of F().So far, I'm with you. This is indeed the question.
Great.
�But if the system under study is closed loop, the the observed relationship
�between d and qo actually reflects 1/E(). That's the behavioral illusion.This would be true if control were perfect.
I don't think so. At least it isn't true in my simulation. The
behavioral illusion, where the relationship between d and qo reflects
only the feedback function, not the system function, occurs for both
very low and very high settings of gain in a simple integral control
model.So it occurs whether control is good or poor.
Let's do the simple analysis
with all the functions being the identity function excepot for the output
gain G.qi = qo + d
qo = Ge = G(r-p) = G(r -qi) = G(r - qo - d)qo/G = r - d - qo
qo(1+G)/G = r - dqo = G(r-d)/(1+G)
The factor G/(1+G) is the sensitivity of qo to changes in d, or the
"compliance" of the system. That compliance, when E() is the identity
function, is purely a property of I(), since in this case I() == G().
I'm better at computer simulations than math. I have written a
simulation of a linear control system (simple integrator) with a
linear feedback function. You can vary the gain (G) of the control
system and the coefficient of the feedback function (E). The model is
very simple. The control system model is:
qo := qo + G(r-qi)
The environment function is:
qi := E(qo) + d
I've run this simulation using different values for G and E while
manipulating d (the IV) and measuring the resulting qo (DV). In every
case, there is a linear relationship between d and qo with a slope
equal to -1/E, the negative inverse of the feedback function. It is
never equal to G, no matter what the value of G is (for G>0).
I'm going to work on improving this spreadsheet and then I'll
distribute it. It's a simple and (I think) pretty clear demonstration
of the behavioral illusion (for linear systems; I might also try a
non-linear system). The simulation shows that the observed
relationship between d and qo, when studying a closed loop system,
reflects_only_ the feedback connection from qo to qi, which is E (in
the form -1/E). The system function, G, that goes from qi to qo, is
completely invisible.
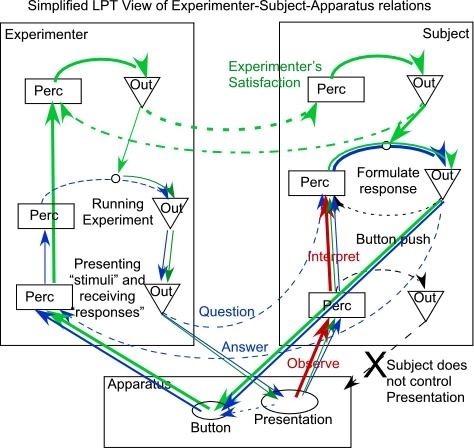
A person doesn't become open loop when they are in a psychophysical
experiment.True. A _person_ doesn't become open loop in a psychophysical experiment.
But the relation betwenn the presentation on trial N and the response choice
on trial N is most definitely open-loop. We thrashed all this out a year or
more ago.
But we apparently got nowhere, which I expect will continue now.
Nevertheless, I'll give it another try. The "presentation" in a
psychophysical experiment is an environmental vaiable, like a tone,
that is independent of the actions of the subject. It is therefore a
disturbance, d. The response is an output, qo. There is never a
connection between qo and d in a control loop. The loop is closed due
to the effect of qo on qi (the controlled variable) where qi is
affected by both qo (closing the loop) and d.
In a psychophysical experiment, qi is usually a relationship between d
(the stimulus) and qo (the response) that the subject is asked to
maintain (control). For example, the subject is asked to say "yes"
when a tone is present and "no" when it's not. The disturbance
variable, d, values are "tone" or "no tone"; the output (qo) variable
values are"yes" and "no". qi is the logical relationship between d and
qo. The subject is asked to keep the following logical relationship
"true" (control for "true"): if d="tone then qo = "yes"; if d = "no
tone" then qo = "no".
My "Power Law" paper (http://www.mindreadings.com/BehavioralIllusion.pdf)
shows how the closed loop might work in a magnitude estimation experiment.Yes, I've referenced this before, several times. But even there, there is no
way that the subject's saying "27" can affect the loudness of the tone to
which the subject has assigned that number.
Of course not. The subject's response, qo, affects the state of the
controlled variable (a relationship between the stimulus, d, and the
response, qo). The control system is closed loop through the
controlled variable, not through the disturbance.
Good, but unless your experiment is set up so that the subject's choice
influences the physical presentation that leads to the choice, that critical
element is open loop.
This "critical element" is always open loop. There is never a direct
effect of qo on d in a control loop.
I'll try to get the behavioral illusion spreadsheet ready soon.
Best
Rick
···
--
Richard S. Marken PhD
rsmarken@gmail.com
www.mindreadings.com