In the linear case, the model
takes the general form:x(k+1) = A x(k) + B u(k) + w(k)where
x is the state of the process (in general avector).
u is some set of parameters of the process that youcan set – operating
knobs and levers. A and B are matrices, constituting a model of thesystem.
w is a random variable with zero mean and knownstandard deviation.
w is sometimes called “system noise”, but what it really is is
a model of the unmodelled behaviour of x.
The Kalman filter says that you
should estimate x by a series y given by:y(k+1) = y(k) + K (z(k+1) - y(k))K is called the Kalman gain, and
says how much faith you should put in the observed value z(k+1) vs. your
previous estimate y(k). (The process gets started by just picking
any value for y(0).)The mathematics of Kalman filters gives a way of computing a value of K
that is optimal, in the sense of minimising the expected error. If
the standard deviation of v is large compared with w, K should be small,
so that you trust the model and only slowly update it from the noisy
observations. If it is the other way round, K should be close to 1,
putting more trust in the observations than in the
model.
The control problem is then to
calculate what trajectory u should take in order to make C x(k) follow a
desired trajectory. This is model-based control. The
fundamental problem of model-based control is the imperfection of
models. Kalman filters are a fix for that, given a model of the
imperfections of the model. An example would be a cruise missile
navigating by GPS.
[From Bill Powers (2007.11.25.0140 MST)]
Richard Kennaway (2007.11.21.1447 GMT) –
…
That makes K into EXACTLY the slowing factor that we use in the output
function of our simple control system models! When I saw a plot of the
actual (noisy) plant state vector versus the predicted state, I thought,
“Shoot, that looks as if they’re just smoothing the noise out
of the state vector.” Now you’re telling me that’s exactly what
they’re doing:
So that part of Modern Control Theory is just concerned with bad models
and noisy observations. I thought it was much more than that, allowing
calculation of the best weights to use for affecting the individual
variables in the state vector and so on, according to various partial
derivatives.
What would I do without you? If that’s all the Kalman filter is about, we
can forget it. We’re back to the basic mistake of trying to calculate
inverse kinematics and inverse dynamics to find the best form for u[k] to
bring some controlled variable its desired state along some preselected
trajectory.
Now we can see how the MCT approach fits into the PCT approach – if I
have this right, I’m going to put this in the book, with reference to a
more rigorous discussion in your appendix, which I hereby request you to
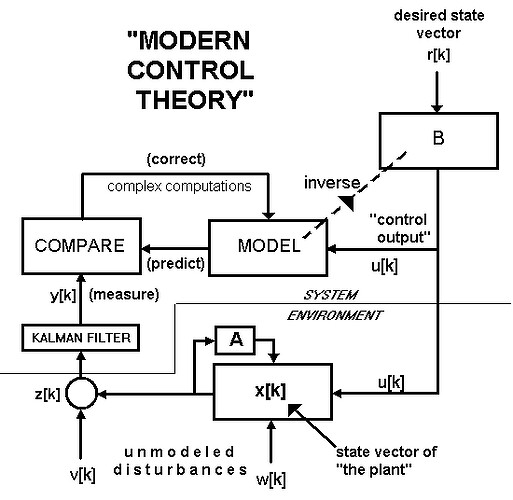
write. Here is the diagram I get from your description. Please correct it
…
The “plant” is the environmental feedback function. The
“state vector” x[k] is the set of variables internal to this
block in the diagram. The vector w[k] is the “system noise”
resulting from internal unmodeled disturances inside the environmental
feedback function. The state vector at time k+1 is the matrix A times
(x[k] + w[k]).
These internal variables, added to external disturbances v[k], generate
an observation vector z[k] = (x[k] + w[k]) + v[k]
The observed state of x[k] is compared with a model’s state, and the
difference is used to correct the model (by calculations not shown in
this diagram). Then the inverse of the model equations is found, and used
to create B, a matrix that converts the desired value r into the
“control output” u[k] that will make x[k] = r[k].
I don’t see any
relevance of the Kalman filter to classical negative feedback control,
other than as a means of noise reduction separate from the control
problem. All the references I’ve found dealing with Kalman filters
and control are about model-based control.
Yes, it looks like a very complicated way to control something, and this
method has to assume that the disturbances are gaussian with a mean of
zero – this system can’t counteract even the low-frequency part of the
disturbance spectrum, because the noise has to be filtered out before the
comparison used to adjust the model.
Does the above diagram fit your understanding of model-based
control?
Best,
Bill P.