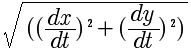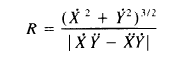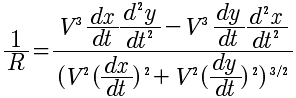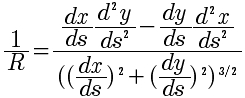[Martin Taylor 2016.08.16.13.13]
[From Rick Marken(2016.08.19.2100)]
I suppose that if you ignore the relevant mathematics and say it's
irrelevant when it is presented to you in outline and also when it
is given in excruciating detail, I suppose you could say that. You
shouldn’t, but there you go. Nothing anyone but you can do anything
about it.
For the few who still might be interested, here's both overview and
detail approaches rolled into one.
Point 1. No description of shape can depend on anything but measures
of space. Time and velocity cannot enter into them.
----- detail follows----
There is a mathematical description of curvature in a Euclidean (x
vs. y) space. Curvature is defined as 1/R, where R is a radius of
curvature (the radius of an “osculating circle”, the circle
equivalent of a tangent straight line).
In the following formulae, "s" means distance along the curve, and
(x, y) is a location in the space. the differential ds in terms of x
and y is given by ds = (dx2 + dy2)1/2 from
basic Euclidean geometry. One can do as is done in the Wikipedia
article on Curvature, divide through this equation by ds and define
an “intermediate variable” or “formal variable” which I will call
“w”. The definition of “w” is

The basic expression for curvature (it's based on computing the
tangent vector acceleration, which we don’t need to go into. If you
re interested, you could look up the actual derivation) is

so we can write
---- end detail----

If we do as Rick does, call the numerator of this fraction "D" and
transpose, we get
w<sup>3</sup> = D*R
or
w = D<sup>1/3</sup>*R<sup>1/3</sup>
Notice that nothing at all in this derivation has any relationship
to time or velocity. Those should not and do not enter into any
formula that is purely about the shape of a curve. And yet we arrive
at a formula for “w” that Rick calls a velocity. Not only that, but
Rick claims “w” to be the velocity that the “power law researchers”
measure in their experiments.
Point 2. Right at the start of this curious set of exchanges, we
pointed out to Rick that he had made a very excusable mistake,
figuring that correcting the mistake would end that particular
discussion, but we were sadly mistaken. The reason that the mistake
is easy to make is that the derivatives in the formula have been
represented in the “dotty” Newtonian notation, and are often taken
to be derivatives with respect to time.
----detail follows----
The problem with this is that the formulae do work if you use time
derivatives, but they do so if and only if you prespecify a velocity
profile along the track of the curve. You can set V as a function of
t (time) or of s (distance along the curve), because they convert
into each other, but you have to set it before you do any other
manipulations. It can be anything, provided that it defines a
one-to-one mapping between t and s.
V(t)<sub>t= t0</sub> = (ds/dt)<sub>t=t0
</sub>or<sub>
</sub>V(s)<sub>s=s0</sub> = (ds/dt)<sub>s=s0</sub>
If you integrate V(t) after time t0 or V(s) after point s0, you get
a mapping of t onto s. For each moment in time there is a
corresponding point along the curve. Those values depends on the
arbitrarily defined V function of t or s, So let’s see (once again)
what we arrive at when we use this arbitrary mapping of t onto s,
starting with the formulae when you take the dot notation as
signifying differentiation with respect to time.
The first formula, which defined our intervening variable "w" now is

The curvature formula becomes

It is perhaps worth noticing at this point that it would be formally
correct to multiply top and bottom by (dt)3 to avoid
having time mentioned in a formula for a description of space, but
we won’t do that because we want to see whether the formula as
written is correct on the assumption that we have specified a
velocity function of either time or distance along the curve. What
we will do is note that in calculus generally, dx/dy = dx/dzdz/dy
and d2x/dy2 = d2x/dz(dz/dy)2 ,
and use these equalities to show that the equation is correct by
deriving it from the second equation above, the basic formula for
curvature, repeated here.
<img alt="" src="cid:part2.EA82C6B3.58EF46B9@mmtaylor.net" height="98" width="245">
Using the equivalences just mentioned, we can write this as

And cancelling out the ds's we get the formula above
<img alt="" src="cid:part5.534D9446.66DB2731@mmtaylor.net" height="98" width="245">
Q.E.D.
Provided we have chosen some arbitrary velocity in advance as a
function of time or space, so that ds/dt has a value, the equation
for curvature with the time derivatives is correct.
----end detail---
It is very easy to ignore the requirement to specify an arbitrary
V(t) or V(s) and think that the two equations, one for the velocity
and one for the curvature, are independent. That’s exactly what Rick
did when he noticed that the denominator of this formula is actually
V3 . He thought that he could then do as we did above for
the formal variable “w”, which has no relation to velocity. So we
follow Rick and do it here, for V, but now we do it knowing that we
pre-set V. Rick calls the numerator of the fraction “D”, so the
equation becomes
1/R = D/V<sup>3</sup>
which immediately gives Rick's favourite equation for determining(!)
the already arbitrarily specified V.
V = D<sup>1/3</sup>*R<sup>1/3</sup>
Notice here that V is the same as the "w" variable we found earlier,
except that the equations were based on time derivatives instead of
distance derivatives. They are incorporated in the “D” variable.
The equation is true, but we can't use it to determine V because in
order to create the equation we had to create the arbitrary V
function before we started. The equation tautologically has V on
both sides, as the proof of correctness of the time-based formula
demonstrates. Alex pointed this out as soon as Rick introduced this
so-called equation, this tautology, but to no avail.
In other words, none of it, since you continue to claim that the
arbitrarily preset variable “V” in the equation above is what people
measure. They don’t. They measure how fast people and other
organisms move along a curving track. Quite a different thing.
Not in the slightest. It
says that your so-called test is a cheat because it uses reference
trajectories whose speed along the curve is defined by the power
law. When you use real data, as you seem to do below, you get what
Alex and many other have found. And what Alex would like to have
explained.
No, there's no implied
relationship between the shape and the speed. There may well be a
relationship in practice, as Alex said when he asked the original
question. His question was why this relation is found in practice
when there is no analytically determined reason for it. One can,
in principle, choose to go fast around the sharp curves and go
slow when there is a flat section. Apparently people don’t usually
do that, and I assume that your data contribute to the mass of
evidence that this is so.
That's good. Without
knowing what you actually calculate, I can’t judge whether these
betas are what is usually computed, but I’ll take your word that
they are. I wonder whether your apparatus had some equivalent of
viscosity?
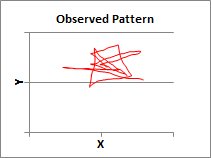
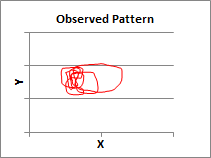
The problem is that your sine waves are sine waves with as a
function of time. The squiggle shapes have no connection with time,
so your comment (and your spreadsheet and your analysis) fails to
make the connection. You don’t need different disturbances, you need
different disturbance velocities . As I have suggested
several times, there are several easy ways to do this without
changing the shapes of either the target squiggle or the
disturbances. You shouldn’t need any new instructions how to do it.
Well, you are saying the same thing in different words. Yes you
must, and no you don’t, or haven’t yet.
You have not, so far as I know, ever demonstrated that your model
produces the power law when the along-track velocity of the target
squiggle does not.
I agree that's what you *should* do. I keep asking you do do
it. I don’t mind if you refuse to do it. I do mind that you keep
claiming that you have done it. It confuses the readership, and I’d
prefer that the CSGnet readership were treated to honest PCT
discussions rather than ones that depend on a mathematical
misunderstanding, however easy that misunderstanding is to make.
Martin
···
Martin Taylor 2016.08.19.14.00)–
MT: But where is the velocity? It's the
along-track velocity of the reference squiggle that is
critical, not its shape.
RM: You say it's "critical". Yet the model accounts for
the data without it.
So as the electrified Dylan said to the fan who yelled
“Judas”, “I don’t believe you”.
MT: But I ask for
the Nth time, where is the along-track speed variation
in the reference trace in your spreadsheet?
RM: Where is it in your model? As I said, there
is no need to put an along-track speed variation in the
reference trace into the PCT model in order to account for
the data (power law). The reference trace is actually a
trajectory – variation over time – not just a shape, by
the way. So a regular old PCT model with fixed or variable
reference accounts for all of the power law data with
which I am familiar.
MT: In the one you
distributed, you use a reference track that, by its
construction from x and y variations that are composed
of sine-waves over time, imposes a 1/3 power law on the
cursor velocity.
RM: This
implies that you accept my explanation of the power law.
RM: Your
statement is also consistent with my explanation of
the power law because it implies that the power
coefficient that is observed in power law studies
depends on the movement pattern (trajectory)
produced.
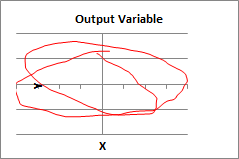
And, indeed, it
does, as can be seen by pressing the “Scribble”
button over and over (which should work on your Mac;
just the “Data collection” macro doesn’t work on the
Mac) and seeing the different estimates of beta for
the different scribbles in the upper right corner.
Just now I got estimates of beta for the different
scribbles that ranged from .25 to .38. The average
for 10 trials was .31.
MT: Bruce says that
even the disturbances are made the same way, so that the
output of any decent control system must conform to the
same power law. It’s forced by the construction, and is
not a property of the movement control system.
RM: It looks to me like you are complaining about the
fact that the model accounts for the data. But maybe you
are saying that somehow the fit to the data is forced by
my choice of disturbances. Perhaps, like Bruce, you think
the use of sine wave disturbances has something to do with
it. So I’d be happy to use different disturbances; let me
know what you would like me to use. But remember Fourier’s
theorem; every disturbance waveform can be represented as
the sum of sine waves of different phases and frequencies.
MT: To test the
model you MUST use a reference track in which the
along-track velocity is independent of the local
curvature.
RM: No, to test the model you must compare the model's
behavior to the behavior of the systems whose behavior you
are trying to understand.
If the model doesn't fit the behavior, perhaps it's
because you haven’t done what you say (used a reference
track in which the along-track velocity is independent of
the local curvature). But my model does fit the data so
your emphatic “MUST” is simply not true.
MT: It's easy to do.
Here’s anothe method to add to the ones suggested
previously. You could have a “squiggle-like” column
listing some arbitrarily varying local velocity in x and
in y, and integrate that to produce the reference
squiggle. If the cursor speed conforms to the 1/3 power
law when the reference speed does not, then you would
really have a significant advance in answering Alex’s
question.
RM: This is not the way I test models. I test models
against actual observations, not against what someone says
should be but hasn’t yet been observed.