More Questions

[Bill_Powers1]

[From Bill Powers (2011.06.17.0723 MDT)]

bob hintz 2011.6.16

I would like to suggest that the controlled variable is the relationship between the participants in the conversation and that the relationship between the speech acts is the method of controlling this relationship.

BP: That is certainly a possible controlled variable. What I diagrammed was the conveyance of a meaning from one person to another, where I am defining meaning as a nonverbal perception indicated by a word or a sentence or a conversation. I say "Is that an orange on the table?" You answer "No, the table is brown," which I perceive as not being an answer to my question. I realize that you didn't hear "on the", so I say it again, enunciating "ON THE" louder and more carefully, and you say ""Oh, sorry, yes, I think that's an orange." Your answer was a disturbance which generated an error, and I tried to correct the error by altering something about my speech output, and your reply then satisfied me that you were answering the question I asked.

A similar thing happened to you: when I asked (apparently) if that is an orange table, you take that as a request for information. Being cooperative, you emit a communciation which to you sounds like an answer to my question. When I say the question again more clearly, you realize that your answer doesn't match the question (wrong relationship of meanings), and correct the error by changing your answer. Since I'm satisfied too, that exchange ends with no error on either side.

I've told this one before but it's relevant. A comedian is asked to do his act for an audience in a Chinese theater. Horrible experience: the comedian complains to his Chinese friend that he couldn't see the audience because of the lighting and absolutely nothing got any laughs. Friend says, "This is my mother. Tell her your best joke." Comedian does. Mother shows huge smile, rocks back and forth holding her sides, doesn't make any noise.

The controlled variable there is a relationship between meanings. The joke hinges on an unexpected meaning, and the expected return communication is applause and laughter. The meaning of silence, when the audience can't be seen, is dislike of the joke. Note that one side of this communication is almost completely nonverbal.

I think it would take a real linguist to look for categories of controlled variables in communications. I can think of examples all day long, but they're probably not all of different kinds. I think the number of different kinds of CVs is probably greater than 2 and less than 100,O00. But Bruce Nevin can probably narrow it down even further.

Best,

Bill P.

[Bob_Hintz]

bob hintz 2011.6.16

The diagram of communication proposed earlier would be much clearer if a t1 is attached to the arrow when the first speaker hears himself speak at the same time that the first listener hears him speak and t2 is attached to the arrows that indicate that the second speaker (formerly the first listener) hears himself speak and the second listener (formerly the first speaker) at the same time hears speak.

In your example, you assumed that the other person was providing an answer and you worked backward to guess at what question it might have been an answer to in order to try again. If he had said, “Today is Tuesday”, you might have wondered if he heard you at all. If you look up and notice that he has a phone to his ear, you may develop a different hypothesis regarding the sense of his speaking.

Anytime we address another person we are organizing our output in the context of some conception of our relationship to that person. Their response will necessarily reveal something about their conception of that same relationship. If their response makes sense to me, I do not experience any error and have no reason to revise my conception. If my initial action made sense to the other person, they experience no error and have no reason to revise their conception either.

Much conversation is primarily focused on confirming, revising or expanding our shared understanding of our on-going relationship with each other. As Boris points out there are lots of different possibilities at any given moment that could be selected by the other person as relevant to understanding any specific speech act and we routinely try to inform others about the context of our talk. This is much easier if we are in the same general space and can point to specific items like a picture.

I have not yet learned how to add drawing to my messages.

bob

···

On Fri, Jun 17, 2011 at 8:57 AM, Bill Powers powers_w@frontier.net wrote:

[From Bill Powers (2011.06.17.0723 MDT)]

bob hintz 2011.6.16

I would like to suggest that the controlled variable is the relationship between the participants in the conversation and that the relationship between the speech acts is the method of controlling this relationship.

BP: That is certainly a possible controlled variable. What I diagrammed was the conveyance of a meaning from one person to another, where I am defining meaning as a nonverbal perception indicated by a word or a sentence or a conversation. I say “Is that an orange on the table?” You answer “No, the table is brown,” which I perceive as not being an answer to my question. I realize that you didn’t hear “on the”, so I say it again, enunciating “ON THE” louder and more carefully, and you say "“Oh, sorry, yes, I think that’s an orange.” Your answer was a disturbance which generated an error, and I tried to correct the error by altering something about my speech output, and your reply then satisfied me that you were answering the question I asked.

A similar thing happened to you: when I asked (apparently) if that is an orange table, you take that as a request for information. Being cooperative, you emit a communciation which to you sounds like an answer to my question. When I say the question again more clearly, you realize that your answer doesn’t match the question (wrong relationship of meanings), and correct the error by changing your answer. Since I’m satisfied too, that exchange ends with no error on either side.

I’ve told this one before but it’s relevant. A comedian is asked to do his act for an audience in a Chinese theater. Horrible experience: the comedian complains to his Chinese friend that he couldn’t see the audience because of the lighting and absolutely nothing got any laughs. Friend says, “This is my mother. Tell her your best joke.” Comedian does. Mother shows huge smile, rocks back and forth holding her sides, doesn’t make any noise.

The controlled variable there is a relationship between meanings. The joke hinges on an unexpected meaning, and the expected return communication is applause and laughter. The meaning of silence, when the audience can’t be seen, is dislike of the joke. Note that one side of this communication is almost completely nonverbal.

I think it would take a real linguist to look for categories of controlled variables in communications. I can think of examples all day long, but they’re probably not all of different kinds. I think the number of different kinds of CVs is probably greater than 2 and less than 100,O00. But Bruce Nevin can probably narrow it down even further.

Best,

Bill P.

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.06.18.14.57NZT)

[From Bill Powers
(2011.06.17.0723 MDT)]

bob hintz 2011.6.16

BP: I think

the number of different kinds of CVs is probably
greater than 2 and

less than 100,O00. But Bruce Nevin can probably
narrow it down even further.

Brilliant, I have created
a drawing to communicate (I agree Bill
there is no better way), what I’m a trying to do. I have shown potentially
as many environmental disturbances I can think of.

I would love to get Bruce’s
narrowed down versions so I can match it up to this diagram.

For multiple individuals just
imagine layers connected back on to each other (maybe like a doughnut) with the
outputs going to multiple individual potential disturbances and back through
the cycle again. Pretty complicated and difficult to picture (I will make a drawing).
That is individual output variables can only connect to multiple individual disturbances.

In this drawing it also allows
for individuals in a feedback relationship just with the natural world. What is
the relationship between D_B
and D_A.? Shrink, destroyed, hit back, sort
of depicts our relationships with the earth at present.

What is the relationship
with D_B and D_A
when control systems are controlling is a very interesting
question?

Would some like to start
adding specific output variables (any) and controlled variables (any)?

Can we start creating a
database of potential controlled variables??

I think we can only
imagine (control in us) of our world if there are disturbances otherwise we can’t
control anything? Disturbances are the environment??? What do you think?

After all it’s all
perception?? (right???).

Regards

Gavin

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz
2011.06.20.12.46NZT)

[From Bill Powers
(2011.06.18.0725 MDT)]

Gavin
Ritz 2011.06.18.14.57NZT

I
have created a drawing to communicate (I agree Bill there is no
better way), what I’m a trying to do. I have shown potentially as many
environmental disturbances I can think of.

I would love to get Bruce’s
narrowed down versions so I can match it up to this diagram.

For multiple individuals just imagine layers connected back on to each other
(maybe like a doughnut) with the outputs going to multiple individual potential
disturbances and back through the cycle again. Pretty complicated and difficult
to picture (I will make a drawing). That is individual output variables can
only connect to multiple individual disturbances.

I don’t think this diagram is right, but you’re making me think about some
things that have just slipped past before.

I agree there’s something not quite
right. There’s also a problem with how the environment will respond. There’s
a sort of discontinuity. In this drawing it will have to flip-flop. As per your
control system nothing can circumvent the controlled variable prior to the
input. I am going to study your response and see if I can understand it.

And will come back with some questions.

Much appreciated, thank you.

Regards

Gavin

In my diagram I have shown one person’s sentences as disturbances of the other
person’s inputs. In yours, however, you have shown a wide variety of
disturbances other than the sentences, and in fact you’ve left out the
connection from one person’s controlled variable to the other one’s
perceptions. I can see the reason for this: I have drawn diagrams that are
quite similar to this (I mistyped that as “disagrams,” but that’s not
a bad word for a disfunctional diagram).
Here’s the problem. A sentence, for its utterer, is a controlled variable. We
monitor the written or spoken sentences we’re producing, often editing them
by saying them again with better wording or organization, sometimes
seeing bad interpretations and adding more sentences to rule them out. There
are lots of environmental variables acting as disturbances, just as you have
drawn them, but we make corrections as we go to keep those disturbances from
affecting the overall communication that we perceive and that goes to the other
person. So a sentence acting as a disturbance to another person’s perceptions
is more than that: it’s a controlled
disturbance. The sentence itself is protected against most disturbances, so it
arrives at the other person’s ears in the same form in which it left the
speaker’s mouth, or reasonably so.
At the same time, of course, there can be uncontrolled disturbances reaching
the listener’s ears – a jackhammer starts pounding on concrete nearby drowns
out the sentences, earwax in the listener’s ears attenuates the sound, echos in
a bare room jumble the sound-waves before they get to the ear. These
disturbances are not affected by the speaker or the listener.
There can also be disturbances at different levels. The tone of voice in which
the sentence is uttered can be perceived as insulting or mocking, the meaning
of the sentence can itself be a disturbance to some other systems: “Do I
smell smoke?”
And of course there are many disturbances that affect other variables the
listener is controlling, such as balance, nutrition, brightness, wealth, the
ecology, and so forth. But in analyzing communication itself, we aren’t talking
about those other control systems.
Now the missing connection, from the controlled variable of the speaker to the
input function of the listener. Look at my diagram, here with some added
detail:
This diagram shows two amorphous clouds of other environmental variables
affected by the speaker and affecting inputs to the listener at some level,
going both ways between communicators. These are uncontrolled effects of the speech and uncontrolled causes of effects on the
listener – uncontrolled by either party shown in the diagram, that is. These
other disturbances have to be removed for the communication to be
“pure”.

I’ve also moved the “cv” designation to the perceptual signal. Now
the little circles in the environment indicate some group of input quantities
(like sound waves or printed characters) involved in control of the CV and
which affect both the speaker and the listener. The little circles can also
represent groups of lower-level perceptions, the environment then including the
lower-level systems below the ones shown. Now the CV can be defined at any
level with less confusion. I have not shown any direct connection from one
speaker’s output to the other’s input, though that could be one case. It would
still be uncontrolled because the speaker does not perceive the effect.

With these additions, we can see that each little circle is a set of variables
involved in controlling a CV, and that if the input functions of the two
parties are organized the same way, the circles will each be perceived as the
same CV by both parties. Of course great confusion arises when the two input
functions are not organized the same way.

What is new about this diagram is mainly that the communication goes not from
the output of one system to the input of the other, but from the input
quantities of one system to the input functions of both systems. As Bob Hintz
noted, the two inputs to each system are really sequential, with memory being
involved so they can be compared: what I’m hearing now in relation to what I
said before. Children soon learn that if they speak while someone else is
talking, they aren’t heard. That’s a lower-level kind of disturbance.

···

[BUSINESS_GAVIN_HERMA]

[From Bill Powers
(2011.06.18.0725 MDT)]

Gavin Ritz 2011.06.18.14.57NZT

I
have created a drawing to communicate (I agree Bill there is no better
way), what I’m a trying to do. I have shown potentially as many
environmental disturbances I can think of.

I would love to get Bruce’s
narrowed down versions so I can match it up to this diagram.

For multiple individuals just imagine layers connected back on to each other
(maybe like a doughnut) with the outputs going to multiple individual potential
disturbances and back through the cycle again. Pretty complicated and difficult
to picture (I will make a drawing). That is individual output variables can
only connect to multiple individual disturbances.

I don’t think this diagram is right, but you’re making me think about some
things that have just slipped past before.
In my diagram I have shown one person’s sentences as disturbances of the other
person’s inputs. In yours, however, you have shown a wide variety of
disturbances other than the sentences, and in fact you’ve left out the
connection from one person’s controlled variable to the other one’s
perceptions. I can see the reason for this: I have drawn diagrams that are
quite similar to this (I mistyped that as “disagrams,” but that’s not
a bad word for a disfunctional diagram).
Here’s the problem. A sentence, for its utterer, is a controlled variable. We
monitor the written or spoken sentences we’re producing, often editing them
by saying them again with better wording or organization, sometimes
seeing bad interpretations and adding more sentences to rule them out. There
are lots of environmental variables acting as disturbances, just as you have
drawn them, but we make corrections as we go to keep those disturbances from
affecting the overall communication that we perceive and that goes to the other
person. So a sentence acting as a disturbance to another person’s perceptions
is more than that: it’s a controlled
disturbance. The sentence itself is protected against most disturbances, so it
arrives at the other person’s ears in the same form in which it left the
speaker’s mouth, or reasonably so.
At the same time, of course, there can be uncontrolled disturbances reaching
the listener’s ears – a jackhammer starts pounding on concrete nearby drowns
out the sentences, earwax in the listener’s ears attenuates the sound, echos in
a bare room jumble the sound-waves before they get to the ear. These
disturbances are not affected by the speaker or the listener.
There can also be disturbances at different levels. The tone of voice in which
the sentence is uttered can be perceived as insulting or mocking, the meaning
of the sentence can itself be a disturbance to some other systems: “Do I
smell smoke?”
And of course there are many disturbances that affect other variables the
listener is controlling, such as balance, nutrition, brightness, wealth, the
ecology, and so forth. But in analyzing communication itself, we aren’t talking
about those other control systems.
Now the missing connection, from the controlled variable of the speaker to the
input function of the listener. Look at my diagram, here with some added
detail:
This diagram shows two amorphous clouds of other environmental variables
affected by the speaker and affecting inputs to the listener at some level,
going both ways between communicators. These are uncontrolled effects of the speech and uncontrolled causes of effects on the
listener – uncontrolled by either party shown in the diagram, that is. These
other disturbances have to be removed for the communication to be
“pure”.

I’ve also moved the “cv” designation to the perceptual signal. Now
the little circles in the environment indicate some group of input quantities
(like sound waves or printed characters) involved in control of the CV and
which affect both the speaker and the listener. The little circles can also
represent groups of lower-level perceptions, the environment then including the
lower-level systems below the ones shown. Now the CV can be defined at any
level with less confusion. I have not shown any direct connection from one
speaker’s output to the other’s input, though that could be one case. It would
still be uncontrolled because the speaker does not perceive the effect.

With these additions, we can see that each little circle is a set of variables
involved in controlling a CV, and that if the input functions of the two
parties are organized the same way, the circles will each be perceived as the
same CV by both parties. Of course great confusion arises when the two input
functions are not organized the same way.

What is new about this diagram is mainly that the communication goes not from
the output of one system to the input of the other, but from the input
quantities of one system to the input functions of both systems. As Bob Hintz
noted, the two inputs to each system are really sequential, with memory being
involved so they can be compared: what I’m hearing now in relation to what I
said before. Children soon learn that if they speak while someone else is
talking, they aren’t heard. That’s a lower-level kind of disturbance.

···

-----Original Message-----
From: Control Systems Group
Network (CSGnet) [mailto:CSGNET@LISTSERV.ILLINOIS.EDU] On Behalf Of Bill Powers
Sent: Sunday, 19 June 2011 3:03
a.m.
To: CSGNET@LISTSERV.ILLINOIS.EDU
Subject: Re: More Questions

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz
2011.06.21.14.30NZT)

[From Bill Powers
(2011.06.18.0725 MDT)]

Gavin
Ritz 2011.06.18.14.57NZT

I don’t think this diagram is right, but you’re making me think about some
things that have just slipped past before.

In my diagram I have shown one person’s sentences as disturbances of the other
person’s inputs. In yours, however, you have shown a wide variety of
disturbances other than the sentences, and in fact you’ve left out the
connection from one person’s controlled variable to the other one’s perceptions.
I can see the reason for this: I have drawn diagrams that are quite similar to
this (I mistyped that as “disagrams,” but that’s not a bad word for a
disfunctional diagram).

Here’s the problem. A sentence, for its utterer, is a controlled variable.

Okay. Is not everything a controlled variable
then? Because if a person is not controlling then nothing happens, so no
controlled variable. If a person is not controlling then there is a controlled variable.
So maybe then there is no such thing as any output variables that effect the
environment. It’s only the controlled variable that disturbs the environment.
Like in the amended drawing, below.

What are all the possible key identities
for the output variable?

Another thing I’m still concerned
about is the nature of individual perceptual disturbances and individual perceptual
environments. Da and Db, because maybe disturbances are very individual as per
the drawing. Not of the nature of the relationship between Da and Db.

For example when two tennis players play
against each other the control is the interval between ball and players (with racket),
so tennis player one sends the ball back (disturbs) player 2, thru Db and the
second player disturbs player one thru Da. The rules are an agreement between
Da and Db that player 1 and player 2 agree to control for.

I don’t know this is not so easy.

We monitor the written or
spoken sentences we’re producing, often editing them by
saying them again with better wording or organization, sometimes seeing bad
interpretations and adding more sentences to rule them out. There are lots of
environmental variables acting as disturbances, just as you have drawn them,
but we make corrections as we go to keep those disturbances from affecting the
overall communication that we perceive and that goes to the other person. So a
sentence acting as a disturbance to another person’s perceptions is more than
that: it’s a controlled
disturbance. The sentence itself is protected against most disturbances, so it
arrives at the other person’s ears in the same form in which it left the
speaker’s mouth, or reasonably so.

At the same time, of course, there can be uncontrolled disturbances reaching
the listener’s ears – a jackhammer starts pounding on concrete nearby drowns
out the sentences, earwax in the listener’s ears attenuates the sound, echos in
a bare room jumble the sound-waves before they get to the ear. These
disturbances are not affected by the speaker or the listener.

Yes okay, but is it possible that even
these uncontrolled disturbances are being controlled, by minor fluctuations in
bodily responses.

There can also be disturbances at different levels. The tone of voice in which
the sentence is uttered can be perceived as insulting or mocking, the meaning

of the sentence can itself be a disturbance to some other systems: “Do I
smell smoke?”

Okay

And of course there are many disturbances that affect other variables the
listener is controlling, such as balance, nutrition, brightness, wealth, the
ecology, and so forth. But in analyzing communication itself, we aren’t talking
about those other control systems.

Yes, okay I see what you mean so minor fluctuations
of control can be ignored.

Now the missing connection, from the controlled variable of the speaker to the
input function of the listener. Look at my diagram, here with some added detail:
This diagram shows two amorphous clouds of other environmental variables
affected by the speaker and affecting inputs to the listener at some level,
going both ways between communicators. These are uncontrolled effects of the speech and uncontrolled causes of effects on the
listener – uncontrolled by either party shown in the diagram, that is. These
other disturbances have to be removed for the communication to be
“pure”.

I’ve also moved the “cv” designation to the perceptual signal. Now
the little circles in the environment indicate some group of input quantities
(like sound waves or printed characters) involved in control of the CV and
which affect both the speaker and the listener. The little circles can also
represent groups of lower-level perceptions, the environment then including the
lower-level systems below the ones shown. Now the CV can be defined at any
level with less confusion. I have not shown any direct connection from one
speaker’s output to the other’s input, though that could be one case. It would
still be uncontrolled because the speaker does not perceive the effect.

Not so sure I’m following
this. With the multiple arrows coming from the disturbance and the other
person’s CV it looks like the feedback loop is being circumvented.

With these additions, we can see that each little circle is a set of variables
involved in controlling a CV, and that if the input functions of the two
parties are organized the same way, the circles will each be perceived as the
same CV by both parties. Of course great confusion arises when the two input
functions are not organized the same way.

What is new about this diagram is mainly that the communication goes not from
the output of one system to the input of the other, but from the input
quantities of one system to the input functions of both systems.

I’m a bit confused. Because it does
seem the feedback loop of the control system is being circumvented.

Kind regards

Gavin

···

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.06.21.14.30NZT)

[From
Bill Powers (2011.06.18.0725 MDT)]

Gavin
Ritz 2011.06.18.14.57NZT

I don’t think this diagram is right, but you’re making me think about some
things that have just slipped past before.

In my diagram I have shown one person’s sentences as disturbances of the other
person’s inputs. In yours, however, you have shown a wide variety of
disturbances other than the sentences, and in fact you’ve left out the
connection from one person’s controlled variable to the other one’s
perceptions. I can see the reason for this: I have drawn diagrams that are
quite similar to this (I mistyped that as “disagrams,” but that’s not
a bad word for a disfunctional diagram).

Here’s the problem. A sentence, for its utterer, is a controlled variable.

Okay. Is
not everything a controlled variable then? Because if a person is not
controlling then nothing happens, so no controlled variable.

This should read: If a
person is controlling then there is a controlled variable.

So maybe
then there is no such thing as any output variables that effect the
environment. It’s only the controlled variable that disturbs the
environment. Like in the amended drawing, below.

What are
all the possible key identities for the output variable?

Another
thing I’m still concerned about is the nature of individual perceptual
disturbances and individual perceptual environments. Da and Db, because maybe
disturbances are very individual as per the drawing. Not of the nature of the
relationship between Da and Db.

For
example when two tennis players play against each other the control is the
interval between ball and players (with racket), so tennis player one sends the
ball back (disturbs) player 2, thru Db and the second player disturbs player
one thru Da. The rules are an agreement between Da and Db that player 1
and player 2 agree to control for.

I
don’t know this is not so easy.

We monitor the written or
spoken sentences we’re producing, often editing them by saying them again
with better wording or organization, sometimes seeing bad interpretations and
adding more sentences to rule them out. There are lots of environmental
variables acting as disturbances, just as you have drawn them, but we make
corrections as we go to keep those disturbances from affecting the overall
communication that we perceive and that goes to the other person. So a sentence
acting as a disturbance to another person’s perceptions is more than that: it’s
a controlled disturbance. The
sentence itself is protected against most disturbances, so it arrives at the
other person’s ears in the same form in which it left the speaker’s mouth, or
reasonably so.

At the same time, of course, there can be uncontrolled disturbances reaching
the listener’s ears – a jackhammer starts pounding on concrete nearby drowns
out the sentences, earwax in the listener’s ears attenuates the sound, echos in
a bare room jumble the sound-waves before they get to the ear. These
disturbances are not affected by the speaker or the listener.

Yes
okay, but is it possible that even these uncontrolled disturbances are being
controlled, by minor fluctuations in bodily responses.

There can also be disturbances at different levels. The tone of voice in which
the sentence is uttered can be perceived as insulting or mocking, the meaning

of the sentence can itself be a disturbance to some other systems: “Do I
smell smoke?”

Okay

And of course there are many disturbances that affect other variables the
listener is controlling, such as balance, nutrition, brightness, wealth, the
ecology, and so forth. But in analyzing communication itself, we aren’t talking
about those other control systems.

Yes,
okay I see what you mean so minor fluctuations of control can be ignored.

Now the missing connection, from the controlled variable of the speaker to the
input function of the listener. Look at my diagram, here with some added
detail:
This diagram shows two amorphous clouds of other environmental variables
affected by the speaker and affecting inputs to the listener at some level,
going both ways between communicators. These are uncontrolled effects of the speech and uncontrolled causes of effects on the
listener – uncontrolled by either party shown in the diagram, that is. These
other disturbances have to be removed for the communication to be
“pure”.

I’ve also moved the “cv” designation to the perceptual signal. Now
the little circles in the environment indicate some group of input quantities
(like sound waves or printed characters) involved in control of the CV and
which affect both the speaker and the listener. The little circles can also
represent groups of lower-level perceptions, the environment then including the
lower-level systems below the ones shown. Now the CV can be defined at any
level with less confusion. I have not shown any direct connection from one
speaker’s output to the other’s input, though that could be one case. It would
still be uncontrolled because the speaker does not perceive the effect.

Not so
sure I’m following this. With the multiple arrows coming from the
disturbance and the other person’s CV it looks like the feedback loop is
being circumvented.

With these additions, we can see that each little circle is a set of variables
involved in controlling a CV, and that if the input functions of the two
parties are organized the same way, the circles will each be perceived as the
same CV by both parties. Of course great confusion arises when the two input
functions are not organized the same way.

What is new about this diagram is mainly that the communication goes not from
the output of one system to the input of the other, but from the input
quantities of one system to the input functions of both systems.

I’m
a bit confused. Because it does seem the feedback loop of the control system is
being circumvented.

Kind
regards

Gavin

···

[Bill_Powers1]

[From Bill Powers (2011l.05.21.0754)]

Gavin Ritz 2011.06.21.14.30NZT –

BP: Here’s the problem. A
sentence, for its utterer, is a controlled variable.

GR: Okay. Is not
everything a controlled variable then? Because if a person is not
controlling then nothing happens, so no controlled variable.

This should
read: If a person is controlling then there is a controlled variable.

BP: That is true.

GR: So maybe then
there is no such thing as any output variables that effect the
environment. It’s only the controlled variable that disturbs the
environment. Like in the amended drawing, below.

BP: The output variable is the means by which control is carried
out. However,

any output has more than one effect – soundwaves heat the air and reach
other people with whom you aren’t communicating, and physical actions
have even more side-effects. That is what all those other arrows are
about.

GR: What are all the
possible key identities for the output variable?
GR: Another thing I’m still
concerned about is the nature of individual perceptual disturbances and
individual perceptual environments. Da and Db, because maybe disturbances
are very individual as per the drawing. Not of the nature of the
relationship between Da and Db.

BP: That depends on the level of organization you’re talking about. If
you’re talking about the lowest level of behavior, the controlled
variable is a force pulling on a tendon attached to a bone or tissue, and
the output variable is the degree of contraction of a muscle attached to
and stretching the tendon and connective tissues. The force is sensed by
Golgi tendon organs located in and around the tendon’s attachments. The
sensory signals travel to spinal motor neurons where they inhibit the
spinal motor neurons that generate the (error) signals that enter the
same muscle. The reference signal enters the spinal motor neuron from
sources closer to the brain, in the excitatory sense.

At higher levels, the output variable may be a movement of a limb like an
arm with a hand, and the controlled variable something like the angle of
a steering wheel. The feedback is proprioceptive and visual. At a still
higher level, the output might be the reference signal sent to the
steering wheel control system, and the controlled variable the visual
relationship of the car to the road as seen through the windshield. And
at a still higher level, the output variable could be the reference
signal specifying where the car should be steered, and the controlled
variable the relationship of the car and driver to a destination city. Of
course at every level of organization there are many different variables
being controlled at the same time, in parallel, by many control
systems.

BP: Disturbances are simply physical variables in the environment that
can affect variables that an organism is controlling. They are the main
reason that control is required in the first place – if there were no
control, they would cause random variations in the variables. The outputs
of the control systems prevent most of those variations from becoming
significant by acting directly on the controlled variables in opposition
to the effects of disturbing variables. When control is good, you would
never know there are any disturbances just from watching (or hearing) the
controlled variables. Demosthenes supposedly practiced locution by
speaking with stones in his mouth. If you’re riding in a car with an
expert driver, you would never know that there is a strong crosswind (a
disturbing variable) blowing the car toward the side of the road –
except by watching the steering wheel, which is turned into the wind by
amounts that vary as the wind varies. The car itself seems unaffected,
precisely because of those variations in steering wheel angle.

GR: For example when
two tennis players play against each other the control is the interval
between ball and players (with racket), so tennis player one sends the
ball back (disturbs) player 2, thru Db and the second player disturbs
player one thru Da. The rules are an agreement between Da and Db
that player 1 and player 2 agree to control for.

BP: It’s a conflict because both players want to win and only one
can do so. Each player tries to hit the ball in such a way that the other
player can’t return it or has to return it in a way that makes it easy to
hit a winner back, which disturbs the other player is trying to
accomplish – the same thing.

BP earlier :
At the same time, of course,
there can be uncontrolled disturbances reaching the listener’s ears – a
jackhammer starts pounding on concrete nearby drowns out the sentences,
earwax in the listener’s ears attenuates the sound, echos in a bare room
jumble the sound-waves before they get to the ear. These disturbances are
not affected by the speaker or the listener.

GR: Yes okay, but is it possible that even these uncontrolled
disturbances are being controlled, by minor fluctuations in bodily
responses.

BP: Yes, of course. It’s not the uncontrolled disturbances
themselves that are controlled, but the variables that the disturbances
might alter. The driver doesn’t control the crosswind, but the position
of the car in its lane, which the crosswind would otherwise affect. And
the fluctations in body response aren’t necessarily minor – they can
require almost all the effort one can generate. The only disturbance
controlled by the speaker is the spoken sentence which is heard by both
speaker and listener. Now that I think of it, the uncontrolled
disturbances should also be shown acting on the speaker’s perceptions.
That would make the di

BP earlier: There can also be
disturbances at different levels. The tone of voice in which the sentence
is uttered can be perceived as insulting or mocking, the meaning

of the sentence can itself be a disturbance to some other systems:
“Do I smell smoke?”

GR: Okay

BP earlier: And of course there are many disturbances that affect other
variables the listener is controlling, such as balance, nutrition,
brightness, wealth, the ecology, and so forth. But in analyzing
communication itself, we aren’t talking about those other control
systems.

GR: Yes, okay
I see what you mean so minor fluctuations of control can be
ignored.

BP: They are kept minor by the varying outputs of the control
systems.

BP earlier: Now the CV can be defined
at any level with less confusion. I have not shown any direct connection
from one speaker’s output to the other’s input, though that could be one
case. It would still be uncontrolled because the speaker does not
perceive the effect.

GR: Not so
sure I’m following this. With the multiple arrows coming from the
disturbance and the other person’s CV it looks like the feedback loop is
being circumvented.

BP: No, it’s just being affected by disturbances. But the CV itself is
varied (by changing the reference signal) if a higher system sees that
the disturbances are distorting the communication. In a noisy
environment, the higher system might increase the loudness of the
sentences, or hyperarticulate to make them more easily understood – or
even write them on pieces of paper, using a different method of
communication, and hold them up for the other person to see.

BP earlier: What is new about
this diagram is mainly that the communication goes not from the output of
one system to the input of the other, but from the input quantities of
one system to the input functions of both systems.

GR: I’m a bit
confused. Because it does seem the feedback loop of the control system is
being circumvented.

BP: It can be circumvented by overwhelming disturbances. When that
happens, higher systems look for a different way of accomplishing the
goals – by writing, or gesturing, or pulling the other person to another
place where communication is more possible. Or by giving up on enlisting
the other person’s aid and doing whatever is to be done without
help.

Best,

Bill P.

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz
2011.06.22.10.44NZT)

[From Bill Powers
(2011l.05.21.0754)]

Gavin
Ritz 2011.06.21.14.30NZT –

GR:
I’m a bit confused. Because it does seem the feedback loop of the control
system is being circumvented.

BP: It can be circumvented by overwhelming disturbances. When that happens,
higher systems look for a different way of accomplishing the goals – by
writing, or gesturing, or pulling the other person to another place where
communication is more possible. Or by giving up on enlisting the other person’s
aid and doing whatever is to be done without help.

GR: This is the part that really confuses
me. If I look at your canonical control system (the one you posted a few days
ago), there is no possibility of any forces coming into the control system
other than directly where the Controlled Variable is. If it goes directly into the
input function (as in the drawing in the last email) the feedback loop is
compromised (it’s outside the feedback loop) and then it’s not a control
feedback system any more.

Overwhelming (and unforeseen) disturbances
looks like to me potential severing of the feedback loop or total blockage of
the feedback loop at the controlled variable. So even if the output variables
are affecting the environment the disturbances from the environment must still
connect to the controlled variable. Otherwise the control system’s
integrity is compromised. (Ie it’s not a control system anymore).

We need to build a model to test these
diagrams?

Or am I missing something?

Regards

Gavin

[Bill_Powers1]

GR: Overwhelming (and
unforeseen) disturbances looks like to me potential severing of the
feedback loop or total blockage of the feedback loop at the controlled
variable.
[From Bill Powers (2011.06.21.2140 MDT)]

Gavin Ritz
2011.06.22.10.44NZT –

GR: This is the part
that really confuses me. If I look at your canonical control system (the
one you posted a few days ago), there is no possibility of any forces
coming into the control system other than directly where the Controlled
Variable is. If it goes directly into the input function (as in the
drawing in the last email) the feedback loop is compromised (it’s outside
the feedback loop) and then it’s not a control feedback system any
more.

BP: When I draw multiple arrows going into the input function,
they stand for multiple inputs v1, v2 … vn. The input function
is

p = Fi(v1, v2 … vn).

In words, this says that the perceptual signal is some function of that
set of input variables. At lower levels, a simple function is a weighted
sum, so the form of Fi could be

p = k1v1 + k2v2 + … kn*vn

If k1 = 1 and k2 = -1 and there are only two inputs, the perceptual
signal is just

p = v1 - v2.

When some of the variables are affected by the actions of the control
system we can designate them as v’s, while other variables that are not
affected by those actions (thus being disturbances) are designated as
d’s. Then the general form of the input function is given this
way:

p = Fi(v1,v2,…vn, d1, d2, … dm)

where there are n “variables” and m
“disturbances”.

That’s how we can indicate that the perception depends on some set of
variables that is part of the feedback loop and some set of disturbances
that is not affected by the output of the control system.

BP: “Severing” and “blockage” are not normally what
disturbances do, but that can happen. Disturbances simply add their
effects to the effects of the system’s own outputs on the controlled
perception. A crosswind from the right results in a force on the car
pushing it to the left. Turning the steering wheel toward the right
results in another force pushing the car to the right. The net rightward
force acting on the car would depend on the steering force minus the wind
force. When the two are equal the car goes in a straight line. A steering
control system automatically works that way. It varies the steering wheel
angle until the steering force equals and opposes the disturbing force
and the car is going straight (or curving in the desired way).

In this kind of case we can draw a controlled variable, the car’s left or
right velocity, as if it were in the environment, and represent it as a
little circle with another arrow from the circle into the input function
of a control system. We would say the input function is detecting the
car’s sidewise velocity and that the control system keeps it at zero, as
if the velocity actually exists in the environment and is simply being
sensed.

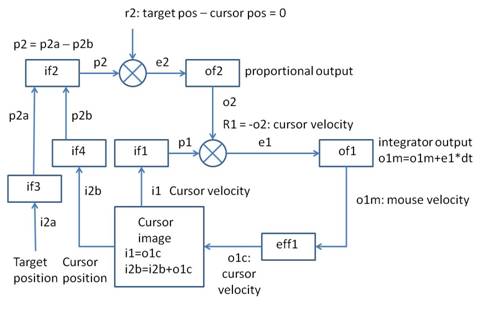
In tracking, we have a cursor that the person can affect with a mouse,
and a target that moves independently of the mouse. Now the controlled
variable is the distance from the cursor to the mouse. We can again
represent this distance as if it were really in the environment, as a
little circle, and show the cursor position as one variable affecting the
distance and the target position as a second variable affecting the
distance. If the target moves upward and is below the cursor, the
distance is decreased, while if the cursor moves upward the distance is
increased. So to compute the distance we say

distance = CursorPosition - TargetPosition

where positive positions are measured in the upward direction from the
origin of the coordinate system. Note that the target position is
formally a “disturbance” because it varies independently of the
action of the control system.

But there is no actual single variable in the environment called a
“distance.” In this case we might say that the input function
receives two variables, one representing the target position and the
other the cursor position. The signal representing one is subtracted from
the signal representing the other to produce a perceptual signal we call
“perceived distance.” Now there is no little circle in the
environment – the subtraction happens inside the input function. That’s
the kind of situation I am representing when I draw multiple input arrows
going into the input function.

Mathematically, it makes no difference whether we show two effects
converging on a little circle in the environment where the effects add
algebraically, or show the two effects entering an input function where
we assume the sensory representations are added in the same way. The
perceptual signal’s magnitude would turn out to be equal to the
algebraic sum of the effects (the sum including the sign of the
variables) in either case.

An “overwhelming” disturbance is simply one that has such a
large magnitude that the control system is physically incapable of
producing the same amount of effect in the opposite direction. In that
special case the control system will generate the maximum output it can
produce, but if the disturbance (and the error) gets even larger, the
control system can’t produce more opposing output. In that case, control
is lost; variations in the disturbance can no longer be met by equal and
opposite variations in the system’s output action until the disturbance
decreases enough. You might then say that the disturbance is
“blocking” or “severing” or “compromising”
control.

GR: So even if
the output variables are affecting the environment the disturbances from
the environment must still connect to the controlled variable. Otherwise
the control system’s integrity is compromised. (Ie it’s not a control
system anymore).

We need to build a model to test these diagrams?

I have tested many models of this kind. In LCS3, Demo 6-1,
“LiveThree”, illustrates it for three control systems, each
affecting and sensing the same three environmental variables which are
also affected by three disturbances. Despite the disturbances and the
strong interactions among the perceptual effects, each control system can
make its own perception closely match any arbitrary reference value while
the other two systems do the same thing with different or the same
reference values.

I have another demo in which up to 500 control systems work the same way:
each system senses a different weighted sum of all 500 environmental
variables, and acts by affecting all 500 variables through another set of
output weighting factors, while maintaining independent control of its
perceptual signal without creating conflict with the other 499
systems.

When you play with demo 6-1 you will see how this works in a simpler
setting. It looks quite impossible, quite magical, but it’s neither. All
that’s required is that the matrix of input weights over all the systems
be the transpose of the matrix of output weights. The transpose of a
matrix is the same matrix with rows and columns interchanged. Richard
Kennaway has shown that this is indeed a sufficient condition for
allowing independent control. I came across it by accident but Richard
actually understands it.

I have also shown that reorganization of the output weights will result
in the same condition of independence given any random selection of
weights in the input function as long as the input matrix is not
singular. I haven’t yet shown that this makes the output matrix the
transpose of the input matrix, but some day we’ll get around to
that.

I hope this is making the meaning of my diagrams clearer, or at least
gives you the sense that there is some fairly well-developed
justification for them. I admit that they’re somewhat ambiguous until
explained in some detail. The problems you see simply show that you’re
trying to understand in some detail, too.

Best,

Bill P.

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.06.23.13.2

[From Bill Powers
(2011.06.21.2140 MDT)]

Gavin Ritz 2011.06.22.10.44NZT –

We need to build a model to test these diagrams?

I have tested many models of this kind.

What I mean is not single individual models
like in Demo 6.1, but multiple individual models interacting together. (Like
the one drawn below).

I have made some comments on your drawing
and made another drawing too for clarity.

What confuses me by your drawing is the
arrows are all outside the control loop, so I can’t see how there can be
any control if this is the case. So I have made another drawing to show what mean.

If we say the controlled variables are
nested, for example I’m going on a journey from A to B in a car. The immediate
controlled variable (CV) is keeping car steady (distance from kerb lets say),
then the intermediate CV is position now to destination B, the major CV meet
friend. Then all CV’s can just be defined as CV’s and the order (or
level) of CV’s can be defined as per mission.

So there is a relationship with the disturbance
variables and the controlled variables (I have just called it for communication
sake) disturbance function. There is also a relationship between Da and Db that
can also be called the personal (or societal function) environmental function. (I
have not drawn that, it’s just a link between Da and Db).

In the drawing I’m trying to keep person
A and B’s control system’s integrity. Dashed area surrounding
person A and person B.

So what this diagram is really saying is that
Perceptual Control Theory says all of science and human knowledge and understanding
are the perceptual relationships between individual environmental disturbances (Da
and Db’s) and the perceptual relationships between perceptual individual disturbances
and individual controlled variables.

Regards

Gavin

···

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.23.17.22NZT)

[From Bill Powers
(2011.06.21.2140 MDT)]

Gavin Ritz 2011.06.22.10.44NZT

···

–

But there is no actual single variable in the environment called a
“distance.”

I think it may well be an actual variable,
in Relativity (or Geometrodynamics) it’s called interval, it’s both
space and time together. Many of our controlled variables see to be “interval”.
Control of Space-time. I sent Galileo’s test to Rick some months ago about control
in relation to the flyball paper he wrote but I don’t think he believed
me.

But you already know this because “Events”
(level 5 HPCT) and interval are also directly related.

Elliot Jaques has found (with tests and evidence) there is a direct relationship
with Time and declarative statements (in language); too, so none of this is too
surprising.

What is surprising and exciting to me is that
PCT may well be able to explain some very confusing paradoxical problems.

In this case we might say
that the input function receives two variables, one representing the target
position and the other the cursor position. The signal representing one is
subtracted from the signal representing the other to produce a perceptual
signal we call “perceived distance.” Now there is no little circle in
the environment – the subtraction happens inside the input function. That’s
the kind of situation I am representing when I draw multiple input arrows going
into the input function.

Mathematically, it makes no difference whether we show two effects converging
on a little circle in the environment where the effects add algebraically, or
show the two effects entering an input function where we assume the sensory
representations are added in the same way. The perceptual signal’s
magnitude would turn out to be equal to the algebraic sum of the effects
(the sum including the sign of the variables) in either case.

Yes I see what you mean, but if speech is
a CV then it is also potentially a perceptual disturbance for person B, C, D or
a whole society. (See my drawing in the last email).

For example “Using Facebook”
is the “output variable” and the controlled variables are “interval”,
“written and photographic language”, the lower order quantities and
the higher order quantities (remains to be worked out). But Facebook (and the
web) is also the medium for disturbances in this case.

An “overwhelming” disturbance is simply one that has such a large
magnitude that the control system is physically incapable of producing the same
amount of effect in the opposite direction. In that special case the control
system will generate the maximum output it can produce, but if the disturbance
(and the error) gets even larger, the control system can’t produce more
opposing output. In that case, control is lost; variations in the disturbance
can no longer be met by equal and opposite variations in the system’s output
action until the disturbance decreases enough. You might then say that the
disturbance is “blocking” or “severing” or
“compromising” control.

Yes that is what I’m saying.

What it looks like to me is that there is
a flowing action from control system to environment to other control systems
and interactions going through different mediums. Sound, light, heat, space-time etc and PCT sort of
allows for any potential flow from control system-environment-control system.

This is a very elegant theory.

Kind regards

Gavin

[Bill_Powers1]

[From Bill Powers (2011.06.23.0017 MDT)]

Gavin Ritz 2011.06.23.13.2 –

BP: I have tested many
models of this kind.

GR: What I mean is not single individual models like in Demo 6.1, but
multiple individual models interacting together. (Like the one drawn
below).
GR: If we say the controlled
variables are nested, for example I’m going on a journey from A to B in a
car. The immediate controlled variable (CV) is keeping car steady
(distance from kerb lets say), then the intermediate CV is position now
to destination B, the major CV meet friend. Then all CV’s can just be
defined as CV’s and the order (or level) of CV’s can be defined as per
mission.

BP: I described one demo in which 500 control systems are simultaneously
affecting a common environment with 500 environmental variables in it,
each system controlling a different function of the same 500
environmental variables.

GR: What confuses me
by your drawing is the arrows are all outside the control loop, so I
can’t see how there can be any control if this is the case. So I have
made another drawing to show what mean…

BP: The arrows are not ALL outside the control loop, but many
definitely are. They influence the controlled variables of each system,
but each system itself produces output with even more effect on those
controlled variables (if they don’t, then as you say the control systems
can’t control). This is realistic. Almost every variable we control is
subject to multiple disturbances. But when we succeed in controlling, we
succeed because we have more effect on the variable than all the
disturbances combined have. That pretty much defines the limits on what
we can control.

BP: What you have to get used to is that every one of these CVs is being
acted upon by multiple unpredictable disturbances at the same time the
driver is steering the car to the destination to meet the friend. It is
hard to see how there could be control when the driver isn’t the only
agency that can apply forces to the car or otherwise disturb the plan.
But that is exactly the beauty of negative feedback control. Just by
monitoring the controlled variable and acting according to deviations
from the reference condition, the driver can keep the variable very close
to its reference condition without even knowing what is causing the
deviations. A good control system can do this so precisely that it’s hard
to notice that there are actually any disturbances present, even though
they may be quite large.

Control is not a matter of producing a specific output that will make the
CV behave as desired. That has been the main idea behind behavioral
models and theories for hundreds of years, but it’s wrong. Control is
carried out by VARYING the output in whatever way is required to cancel
the sum of all effects from multiple disturbances, while producing in
addition the amount of effect needed to maintain the controlled variable
in a specific reference condition. Such a complex-seeming result! But
it’s achieved in an extraordinarily simple way by a closed negative
feedback loop.

GR: So there is a
relationship with the disturbance variables and the controlled variables
(I have just called it for communication sake) disturbance function.

BP: This is exactly what there is NOT when control is working well. The
crosswind blows faster and slower from this direction and that, yet the
position of the car in its lane, if the driver is Mario Andretti’s
offspring, hardly varies at all. All the disturbance function does is to
allow you to compute how the CV would change when disturbed if there
were no control system acting. But it does not change that way.

GR: There is also a
relationship between Da and Db that can also be called the personal (or
societal function) environmental function. (I have not drawn that, it’s
just a link between Da and Db).
GR:In the drawing I’m trying to
keep person A and B’s control system’s integrity. Dashed area surrounding
person A and person B.
GR: So what this diagram is
really saying is that Perceptual Control Theory says all of science and
human knowledge and understanding are the perceptual relationships
between individual environmental disturbances (Da and Db’s) and the
perceptual relationships between perceptual individual disturbances and
individual controlled variables.

BP: How the disturbances are related to each other makes no difference to
the control system. All that matters is the sum of all disturbances that
are acting on the CV – what they do to each other is irrelevant. In PCT
all control systems are assumed to control just one dimension of
variation; for control of position or velocity or force in three
dimensions, for example, three control systems are required. This means
that disturbances, however many there are or how they interact, can only
tend to increase or decrease the value of the controlled variable. And
the action of the control system needs only to decrease or increase the
value of the controlled variable to leave a zero net change. Nearly
zero.

BP: You’re trying to shield the control systems from disturbances, but
you don’t need to do that. The whole point is that they can control in
spite of disturbances, and they don’t even have to know what is causing
the unwanted changes in the CV. They detect the changes and act to oppose
them before the changes have become significant. It looks as if the
disturbances aren’t reaching the controlled variable, but they are. Their
effects are just being cancelled by equal and opposite changes in the
control system’s output.

BP: It’s a little early in human history for such grand sweeping
generalizations, especially when they ignore all kinds of knowledge that
doesn’t fit them (like the orbit of Mars). On the other hand, you can
define your terms so they will fit any situation at all, but that makes
the generalization worthless. It can’t differentiate one situation from
another.

It’s better to try to understand things a little at a time, because when
you do that you find that what you’re trying to understand changes before
you actually reach that goal and you end up somewhere you hadn’t
anticipated – usually a better place.

Best,

Bill P.

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.06.24.11.06NZT)

[From Bill Powers
(2011.06.23.0017 MDT)]

Gavin Ritz 2011.06.23.13.2 –

BP: I have tested many
models of this kind.

GR: What I mean is not single individual models like in Demo 6.1, but multiple
individual models interacting together. (Like the one drawn below).

BP: I described one demo in which 500 control systems are simultaneously
affecting a common environment with 500 environmental variables in it, each
system controlling a different function of the same 500 environmental
variables.

Yes I see that but it’s not
interacting control systems. I want to see what the environmental interactions look
like. Probably the same I guess.

GR: What confuses me by your drawing is the
arrows are all outside the control loop, so I can’t see how there can be
any control if this is the case. So I have made another drawing to show what
mean…

BP: The arrows are not ALL outside the control loop, but many
definitely are. They influence the controlled variables of each system, but
each system itself produces output with even more effect on those controlled
variables (if they don’t, then as you say the control systems can’t control).
This is realistic. Almost every variable we control is subject to multiple
disturbances. But when we succeed in controlling, we succeed because we have
more effect on the variable than all the disturbances combined have. That
pretty much defines the limits on what we can control.

Yip got it

GR: If
we say the controlled variables are nested, for example I’m going on a
journey from A to B in a car. The immediate controlled variable (CV) is keeping
car steady (distance from kerb lets say), then the intermediate CV is position
now to destination B, the major CV meet friend. Then all CV’s can just be
defined as CV’s and the order (or level) of CV’s can be defined as
per mission.

BP: What you have to get used to is that every one of these CVs is being acted
upon by multiple unpredictable disturbances at the same time the
driver is steering the car to the destination to meet the friend. It is hard to
see how there could be control when the driver isn’t the only agency that can
apply forces to the car or otherwise disturb the plan. But that is exactly the
beauty of negative feedback control. Just by monitoring the controlled variable
and acting according to deviations from the reference condition, the driver can
keep the variable very close to its reference condition without even knowing
what is causing the deviations. A good control system can do this so precisely
that it’s hard to notice that there are actually any disturbances present, even
though they may be quite large.

Control is not a matter of producing a specific output that will make the CV
behave as desired. That has been the main idea behind behavioral models and
theories for hundreds of years, but it’s wrong. Control is carried out by
VARYING the output in whatever way is required to cancel the sum of all effects
from multiple disturbances, while producing in addition the amount of effect
needed to maintain the controlled variable in a specific reference condition.
Such a complex-seeming result! But it’s achieved in an extraordinarily simple
way by a closed negative feedback loop.

Yes I’ve got this.

GR: So
there is a relationship with the disturbance variables and the controlled
variables (I have just called it for communication sake) disturbance function.

BP: This is exactly what there is NOT when control is working well. The
crosswind blows faster and slower from this direction and that, yet the
position of the car in its lane, if the driver is Mario Andretti’s
offspring, hardly varies at all. All the disturbance function does is to allow
you to compute how the CV would change when disturbed if there were no control system acting.
But it does not change that way.

Okay.

GR:
There is also a relationship between Da and Db that can also be called the
personal (or societal function) environmental function. (I have not drawn that,
it’s just a link between Da and Db).

BP: How the disturbances are related to each other makes no difference to the
control system. All that matters is the sum of all disturbances that are acting
on the CV – what they do to each other is irrelevant. In PCT all control
systems are assumed to control just one dimension of variation; for control of
position or velocity or force in three dimensions, for example, three control
systems are required. This means that disturbances, however many there are or
how they interact, can only tend to increase or decrease the value of the
controlled variable. And the action of the control system needs only to
decrease or increase the value of the controlled variable to leave a zero net
change. Nearly zero.

Yip okay

GR:In
the drawing I’m trying to keep person A and B’s control
system’s integrity. Dashed area surrounding person A and person B.

BP: You’re trying to shield the control systems from disturbances, but you
don’t need to do that. The whole point is that they can control in spite of
disturbances, and they don’t even have to know what is causing the unwanted
changes in the CV. They detect the changes and act to oppose them before the
changes have become significant. It looks as if the disturbances aren’t
reaching the controlled variable, but they are. Their effects are just being
cancelled by equal and opposite changes in the control system’s output.

Yip I got this too.

GR: So
what this diagram is really saying is that Perceptual Control Theory says all
of science and human knowledge and understanding are the perceptual
relationships between individual environmental disturbances (Da and Db’s)
and the perceptual relationships between perceptual individual disturbances and
individual controlled variables.

BP: It’s a little early in human history for such grand sweeping
generalizations, especially when they ignore all kinds of knowledge that
doesn’t fit them (like the orbit of Mars). On the other hand, you can define
your terms so they will fit any situation at all, but that makes the
generalization worthless. It can’t differentiate one situation from another.

It’s better to try to understand things a little at a time,
because when you do that you find that what you’re trying to understand changes
before you actually reach that goal and you end up somewhere you hadn’t
anticipated – usually a better place.

That’s what in essence PCT says. It’s
all perception albeit agreed or disagreed in control of perception. No matter
what angle I look from that’s what PCT says. Unless I have it totally
wrong.

Orbit of Mars I thought was well worked
out and any deviations from classical mechanics are well explained by Geometrodynamics.
Do you know what doesn’t fit the orbit of Mars?

Regards

Gavin

[Bill_Powers1]

[From Bill Powers (2011.06.26.1100)]

Gavin Ritz 2011.06.24.11.06NZT –

GR:
Orbit of Mars I
thought was well worked out and any deviations from classical mechanics
are well explained by Geometrodynamics. Do you know what doesn’t fit the
orbit of Mars?

What doesn’t fit the orbit of Mars is this:

"GR: So what
this diagram is really saying is that Perceptual Control Theory says all
of science and human knowledge and understanding are the perceptual
relationships between individual environmental disturbances (Da and Db’s)
and the perceptual relationships between perceptual individual
disturbances and individual controlled variables. "

That wouldn’t get you very far toward sending a probe to land on
Mars. And what the heck is geometrodynamics?

Best,

Bill P.

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.06.28.10.35NZT)

[From Bill Powers
(2011.06.26.1100)]

Gavin Ritz 2011.06.24.11.06NZT –

GR: Orbit of Mars I thought was well worked out and any deviations from
classical mechanics are well explained by Geometrodynamics. Do you know what
doesn’t fit the orbit of Mars?

What doesn’t fit the orbit of Mars is this:

"GR: So what this diagram is really saying is that
Perceptual Control Theory says all of science and human knowledge and
understanding are the perceptual relationships between individual environmental
disturbances (Da and Db’s) and the perceptual relationships between
perceptual individual disturbances and individual controlled variables. "

That wouldn’t get you very far toward sending a probe to land on
Mars.

Well you said it, and I’m agreeing
in just a slightly strange manner. It’s all perception.

And what the heck is
geometrodynamics?

The study of gravitation using Einstein’s Theory of
Relativity. The most common text book on this is Gravitation by Wheeler, Misner
and Thorne.

I guess that that’s just perception;
you were unaware of this field, so it was no disturbance for you. So my
statement above is not that weird, in fact it bares out this point rather
nicely.

Regards

Gavin

Best,

Bill P.

[BUSINESS_GAVIN_HERMA]

(Gavin Ritz 2011.06.28.15.17NZT)

[From Bill Powers
(2011.06.26.1100)]

Gavin Ritz 2011.06.24.11.06NZT –

"GR: So what this diagram is really saying
is that Perceptual Control Theory says all of science and human knowledge and
understanding are the perceptual relationships between individual environmental
disturbances (Da and Db’s) and the perceptual relationships between
perceptual individual disturbances and individual controlled variables. "

I relation to this statement, I was trying
to build mathematical categories of the external environment, which is important
(well I think so), to the other discussions on economics. I am trying to create
a mathematical model of the external environment and it shows the environmental
feedbacks really quite well from the drawing you did.

Here is the very strange thing moving from
the internal part of the control system to the external part in interaction with
another control system, I found that there is an impasse in terms of the sets (objects)
and their variables (elements) and the functional transformation (arrows) of
these elements. Almost like a flip-flop the variables sort of become the function,
this is totally strange and impossible. And my first thoughts went to the problem
of Heraclitus (Becoming) and Parmenides (Being). Which also relates to the first bookkeeping rule of
conceptual mathematics (objects and arrows)?

I have no way of trying to resolve this
problem.

Maybe we live in a mirage. (That’s a
joke).

Anyway I forgot to mention this some days
ago, been a bit snowed under moving my business to Sydney Australia.

Regards

Gavin

[chadtgreen]

[From Chad Green (2011.06.30.1213 EDT)]

Gavin, to my mind you are describing the paradoxical nature of reality.

Its manifestation has many forms depending on when, where and how you care to look for it.

To explore the concept further, I'd recommend this article by David Snowden:

Complex acts of knowing: Paradox and descriptive self-awareness
http://www.cognitive-edge.com/ceresources/articles/13_Complex_Acts_of_Knowing_paradox_and_descriptive_self-awareness.pdf

Here's a question for you: What exists beyond paradox?

Perhaps you can enlighten the rest of us if you spend some time exploring the inner product spaces: Space (mathematics) - Wikipedia.

Warm regards,
Chad

Chad Green, PMP
Program Analyst
Loudoun County Public Schools
21000 Education Court
Ashburn, VA 20148
Voice: 571-252-1486
Fax: 571-252-1633

Gavin Ritz <garritz@XTRA.CO.NZ> 6/27/2011 11:37 PM >>>

(Gavin Ritz 2011.06.28.15.17NZT)

[From Bill Powers (2011.06.26.1100)]

Gavin Ritz 2011.06.24.11.06NZT --

"GR: So what this diagram is really saying is that Perceptual Control Theory
says all of science and human knowledge and understanding are the perceptual
relationships between individual environmental disturbances (Da and Db's)
and the perceptual relationships between perceptual individual disturbances
and individual controlled variables. "

I relation to this statement, I was trying to build mathematical categories
of the external environment, which is important (well I think so), to the
other discussions on economics. I am trying to create a mathematical model
of the external environment and it shows the environmental feedbacks really
quite well from the drawing you did.

Here is the very strange thing moving from the internal part of the control
system to the external part in interaction with another control system, I
found that there is an impasse in terms of the sets (objects) and their
variables (elements) and the functional transformation (arrows) of these
elements. Almost like a flip-flop the variables sort of become the function,
this is totally strange and impossible. And my first thoughts went to the
problem of Heraclitus (Becoming) and Parmenides (Being). Which also relates
to the first bookkeeping rule of conceptual mathematics (objects and
arrows)?

I have no way of trying to resolve this problem.

Maybe we live in a mirage. (That's a joke).

Anyway I forgot to mention this some days ago, been a bit snowed under
moving my business to Sydney Australia.

Regards
Gavin

[Bill_Powers1]

[From Bill Powers (2011.06.15.2230 M<DT)]

Gavin Ritz 2011.06.16.16.20NZT –

GR: This is the only
way I can see two independent Control Systems interacting and keeping the
other Control Systems integrity intact.???

Help guys ???

So multiple control systems should look like a layered honey
comb???, kneaded and folded too???

BP: Interesting. As you draw it, the input variable each person is
controlling (some aspect of a communication) does not affect the other
person. Only the outputs that produce the communication do. It’s very
helpful to see this drawn out.

The basic problem here is that control is multi-layered and when only a
single layer is shown, you have to specify what level is represented. If
we say that the controlled variable is the meaning of a sentence, then
each person adjusts the sentences being emitted until the meaning
perceived by the person sending the message represents the intended
meaning (a meaning being some nonverbal perception, usually). In the
diagram below I assume one more implicit level: a relationship between
the meaning one person intends to send and the meaning derived from what
the other person sends. The perceptual signal is shown at the
relationship-between-meanings level. So the (multi-layered) perceptual
input function of each person receives two inputs consisting of
sentences, one the sentences that the person is transmitting, and the
other the sentences being transmitted by the other person. Each sentence
input is converted into a meaning in the input function box and the
output of the box is a relationship between the meanings. So there are
lots of levels below the ones actually shown in this diagram. This is
very similar to Martin Taylor’s Layered Protocol diagrams but perhaps
with more detail shown.

I’ve shown the CV for each system as a circle in the environment between
them, but that’s just a convenient fiction since CV is always defined by
the input function in use. We can say that the circles represent some
collection of physical variables in the environment from which the input
functions ultimately derive the states of the respective CVs.

So the story now is that each person is controlling a relationship
between the meanings they are trying to communicate to the other person
and the meanings derived from sentences the other person is communicating
back. Technically, the latter communication is a disturbance, because it
affects the controlled relationship between meanings independently of the
receiving person’s own outputs. Each person can correct errors in the
relationship between meanings by altering the meanings that person is
sending to himself and – he hopes – the other person.

How should we say this? How about: Each person emits sentences that
affect meanings perceived by the other, and receives from the other
person sentences perceived as meanings, and at some level is trying to
control a relationship between meanings. That seems to wrap up the
essentials in a general way – a more specific organization would need
levels to be shown in each person.

Obviously when more than two actors are involved things rapidly get more
complex. Each person derives meanings from sentences by referring to his
own private experiences, which may or may not have a close resemblance to
the experiences of others. We’ve all seen one sort of result of this on
TV: a collection of experts all yelling simultaneously at each other and
producing noisy chaos. Another example is one person lecturing to a room
full of other people, the words evoking different private meanings taken
from the experiences of each member of the audience. This is one reason I
always organize my talks around demonstrations; there’s a better chance
that we’re all translating the words into similar experiences if we don’t
just rely on words.

Incidentally, this also explains why you got a more informative response
this time – you showed us what you meant. A picture is worth a thousand
words.

Best,

Bill P.

(Attachment 4d244a.jpg is missing)

(Attachment 4d262e.jpg is missing)

[Bill_Powers1]

[From Bill Powers (2011.0.6.16.0925 MDT)]

Gavin Ritz 2011.06.16.18.04NZT

I can only
see it working like this if it is to be consistent with your Control
System. They way you have it below confuses me because the feedback is
severed, like that.

Here it is in more detail. I’ve labeled the two control loops. The
middle part of the diagram is in the environment. Each person perceives
both his own and the other person’s spoken sentences. Each person varies
the sentence he is emitting so as to maintain the desired relationship
between the meaning he perceives in his output sentences and the meaning
he perceives in the sentences the other person is emitting. Only the
highest level in each person is shown, with lower levels and their
control loops being hidden. The reference input is the desired or
intended relationship.

Note that still a higher level would be needed to control for
“understanding” on the part of the other person, which would be
perceived in many instances of (remembered) relationships between one’s
own sentences and the other person’s.

Best,

Bill P.

(Attachment 648769.jpg is missing)