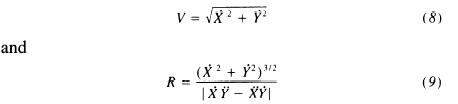···
Alex Gomez-Marin (2016.09.08. 2244)
AGM: Rick, that is what you are doing with your derivation. Let’s suppose that Y=aX^3 (I just made up this equation). Now you say that d=aX and write Y=d*X^2, so then you think you proved that there is a power-law of exponent 2 between Y and X?! If so, then you can rearrange any equation by defining a term “d”, then forget that it is NOT a constant, and get whatever Y-X relation.
RM: It’s not quite the same as what I do. I didn’t factor d out of another expression. But I can use your equation as an analogy to the problem with the power law. You new expression can be written as a linear equation by taking the log of both sides:
log (Y) = 1.0* log (d) + 3 * log(X)
RM: To make this analogous to the power law case we will make a variable along with X so that d is the product of two variables: d = X * a. Now let’s say some researchers have reason to believe that there is a power relationship between d and Y with a coefficient that is >1.0. So they measure d and Y and do a log-log regression using the following regression equation:
log (Y) = a + b*log(d)
RM: What they will find is that the coefficient, b, of log (d) is always > 1.0. The regression always gives a biased estimate of the coefficient of d (1.0) because Y is a function of both d and X. So leaving X out of the regression equation results in the wrong estimate of the true coefficient of d, which is 1.0.
RM: This is exactly analogous to what is happening in the case of the power law. The true relationship (in linear form) between R and V is:
log (V) = 1/3* log(R) + 1/3*log(V^3/R)
RM: In this case I’ve written D as V^3/R since that way R shows up as part of both predictor variables. Power law researchers are doing this regression using only the variable R:
log (V) = a + b*log(R)
RM: The result is that they are getting a biased estimate of the true value of the coefficient of R, which s 1/3. The regression using only R as a predictor will give an accurate estimate of this coefficient – 1/3 – only for data (trajectories) where the covariance of R with V^3/R (the variable formerly known as D) is 0.0.
AGM: And, yes, my original question is what Martin just rephrased.
RM: Well, then it’s not a good question because it makes an assumption that goes beyond the data (the data being the power law). The assumption it makes is that the observed phenomenon is a result of controlling some variable. But there is no evidence in the data that control is going on.
AGM: But if you think your kindergarten flawed mathematics combined with the ad hoc decision that any power-law is more than an illusion, but a phenomenon not worthy of study, then why all this fuzz?
RM: Because power law researchers interpret the power law as a slowing of action in response to increased curvature when it’s not. They are succumbing to a version of the behavioral illusion and developing complex mathematical models to explain why action slows at curves when this is not what is actually happening. A control theory analysis of the situation shows that this couldn’t be what they are seeing (you can’t see the disturbance – curvature-- and the reaction to that disturbance – velocity – in the variations of a single variable) and my statistical analysis shows what they actually are seeing.
AGM: One thing is clear, given the empirical non-trivial relation between speed and curvature found in humans for more than 40 years now, and my recent discovery in another species (the fly), there is a huge opportunity to find out the perceptual origin of that motor relation.
RM: But both Kent and I have presented the perceptual control model that produces movement trajectories that result in a power law relationship between curvature and velocity. It’s just that no body seemed to like it. Well, they did like it when Kent presented it but they like Kent better than me;-)
Best regards
Rick
–
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers
VH: Sorry! The planets velocity is higher with increasing curvature! This is dangerous topic?!
From: Huddy, Vyv
Sent: 08 September 2016 21:18
To: csgnet@lists.illinois.edu
Subject: Re: My Dinner with Andre
Vyv Huddy (2016.8.9.2016)
[From Rick Marken (2016.09.08. 1300)]
RM: The power law is a property of movement trajectories, having nothing to do with how those trajectories are produced. You will find a nice 1/3 power law, for example, for the orbits of the planets. The cause of that movement trajectory, as I’m sure
you know, is gravity.
VH: Not sure about that the orbital speed of Mercury is faster than that of planets further out? Which gradually move more slowly? That is velocity is lower with increasing curvature?
http://nssdc.gsfc.nasa.gov/planetary/factsheet/
VH: Is this to with Kepler’s third law, which the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit? So I think this
is the opposite of the biological power law?
Best
Rick
On Thursday, 8 September 2016, Martin Taylor mmt-csg@mmtaylor.net wrote:
[Martin Taylor 2016.09.07.23.15]
Answering two e-mails in one.
[From Rick Marken (2016.09.07.1420)]
That’s probably true, but it has nothing to do with the problem. Nobody has asked how organisms produce movement trajectories.
If how organisms produce particular trajectories is a problem you want to address, that’s great, but I thought we had all this time been talking about Alex’s question, which can be paraphrased as “Given that an organism produces a particular trajectory, and
that under some conditions the velocity of motion along the trajectory at a point is correlated with a power function of the local curvature at that point, under what conditions does that power function take on any particular value when the correlation is
high, and what is being controlled that makes this happen?”
[From Rick Marken (2016.09.07.1710)]
I don’t know anyone who has said it is false. I certainly haven’t, because it is demonstrably correct. It says V = V, because D is V3/R. It’s just irrelevant.
Which is what everyone has been telling you for goodness knows how long. It’s irrelevant because the V in the formula for curvature is a purely arbitrary variable inserted only so that people can more easily think about movement along the trajectory, and it
also helps one to visualize the concept of “angular velocity” (V(s)/R(s)). V(s) can take on any value at any point “s” on the curve and the algebra still works. V = V everywhere.
The question being asked has to do not with a generic and arbitrary V(s), but with just one observation of how some organism speeded up and slowed down during one particular pass along the trajectory. Since the algebra works for any V(s) at all, it is tells
you nothing about this particular V(s). We have to look elsewhere for the reason why this V(s) happened to be the function of “s” that was observed.
Martin
–
Richard S. Marken
“The childhood of the human race is far from over. We have a long way to go before most people will understand that what they do for others is just as important to their well-being as what they do for themselves.” – William T. Powers
RM: The first step in the study of how organisms produce movement trajectories should be the determination of whether or not the trajectories that are observed are purposefully produced – whether or not the movement trajectory or some
aspect thereof is a controlled variable.
Alex Gomez-Marin (2016.09.07.1134)
AGM: Rick, I really really liked what you say in the last email until you jump from a conscious and clear explanation onto an ad hoc statement which is false: "It turns out that there is a mathematical relationship between the different measures of the controlled variable – curvature and velocity–
that perfectly accounts for the “power law” relationship between these variables that is observed in studies of movement trajectories.
" FALSE FALSE FALSE! But you don’t care.
RM: I do care. But no one has shown me that what I’ve found is false. I would be grateful if you would try to show me again why my derivation is false. Again, I assume these are the formulae that can be used to compute V and R:
RM: Replacing V^2 in the numerator for R I end up with the formula that everyone seems to think is wrong:
V = D1/3 *R1/3 (1)
where D is |dX/dtd2Y/dt -d2X/dtdY/dt| ,
RM: I think the algebra is unquestionably correct. But what also convinces me that this is a correct analysis is that I have replicated all the results reported in the power law papers using the above as the computational formulae for V and R above and
equation (1) explains all the deviations of the observed power coefficients from 1/3.
RM: But I would like to know why you (and nearly everyone else apparently) thinks this mathematical analysis is false.