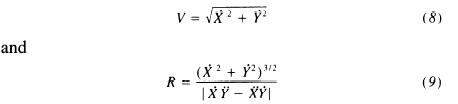My Dinner with Andre

[rsmarken]

[From Rick Marken (2016.09.03.1455)]

RM: Actually it was my wife and I who had dinner with Gary Cziko and his lovely wife. But after dinner Gary and I broke away to have our own “Dinner with Andre” discussion because it turns out Gary has been monitoring the power law discussion on CSGNet (he said he even posted some comments on it but I haven’t seen any; has anyone else?) and he asked some very challenging questions about my analysis, which I am still mulling. But the most important thing I learned from our discussion was that as radius of curvature, R, increases, curvature decreases! So now I know why everyone keeps saying that the power law shows that movement slows down through curves. The power law says that as R increases tangential velocity, V, increases. But since an increase in R is actually a decrease in curvature, the power law means that as curvature decreases velocity increases (or, conversely, velocity decreases as curvature increases, just as everyone says).

RM: [There is still a problem for me with the fact that the power relationship between curvature, measured as C (1/R), and angular velocity, measured as A (V/R), still seems to show an increase in velocity (A) with curvature © since larger values of C now mean greater curvature and larger values of A mean greater speed around a curve). But one thing at a time for me (Gary can apparently handle many things at a time, being as he is, an incredible polymath – multi-instrument musician, multi-sport sportsman, multi-language linguist, multi -book writer and multi-grandchild grandfather ; ironically the only thing he stinks at is math;-)

RM: Just to check things out, when I got home I used my spreadsheet to create ellipses where the velocity of movement was fast through the most curved part of the ellipse and slow through the least curved part. I used an ellipse because when I create elliptical movement in the usual way – by plotting a sine and cosine wave of different amplitude against each other – I get an estimate of the power coefficient relating R to V of exactly .33 with an R^2 of 1.0. When I speed up movement through the curve the power coefficient relating R to V is -.71, which is consistent with the fact that speed was increased through the curves. But the R^2 for the fit of this power law was only .05!! When the D variable (what Richard Kennaway described as “the magnitude of the cross product of V =
(Xdot,Ydot) and the acceleration Vdot = (Xdotdot,Ydotdot)” ) was included in the analysis, the power coefficient of R was .33 and R^2 was 1.0.

RM: Since it is perfectly possible for people to move fast through tight curves and more slowly through gradual curves, this little experiment shows that it is mathematical properties of the movement itself and not how the movement was produced that determines whether or not the movement is fit by a power law – and what the coefficient of the power law will be. What seems to determine the fit of the power law to any movement depends on how the aspect of that movement that is measured as D – the cross product of velocity and acceleration – varies throughout the movement. But now my aim is to demonstrate that this is true with real movement data and figure out what it is about movements that leads to variations in the cross product (D) that affect the fit of the power law to the data.

Best regards

Rick

···

Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[MartinT]

[Martin Taylor 2016.09.04.16.00]

[From Rick Marken (2016.09.03.1455)]

      RM: Actually it was my wife and I who had dinner with Gary

Cziko and his lovely wife. …But the most important thing I
learned from our discussion was that as radius of curvature,
R, increases, curvature decreases! …

      RM: [There is still a problem for me with the fact that the

power relationship between curvature, measured as C (1/R), and
angular velocity, measured as A (V/R), still seems to show an
increase in velocity (A) with curvature (C) since larger
values of C now mean greater curvature and larger values of A
mean greater speed around a curve).

These are two rather shocking statements, considering that both of

the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months
that your analysis of the situation was the only correct one.

It seems that an introductory explanation is in order, simpler than

Bruce and I have offered before, when we (or at least I) believed
you understood these elementary fundamental facts about curvature.
It’s no wonder that our explanations rolled off like water off a
duck’s back! So here goes.

Curvature is _defined_ as 1/R where R is the radius of curvature of

what is called an “osculating circle”. What is an osculating circle?
It has a similar relation to the curve as does a tangent line.

![OsculatingCircle.jpg|630x641](upload://71ZapFYqLdzMfm51Fu8k9qkuDXz.jpeg)

The "curve" in this diagram is a parabola, but that's irrelevant to

the issues at hand. The figure shows an osculating circle for that
particular curve at the point we may call “s=0”. "s, then is the
distance along the curve from that point. It so happens that the
circle matches the parabola very closely for quite a long distance
away from the actual tangent point, a fact that might be relevant to
Alex’s problem.

At some small distance "ds" along the curve (the diagram shows ds as

a large distance, for clarity), the angle at the centre of the
circle between the radii that meet the circle at s=0 and at s=ds is
dθ. dθ in radians is exactly equal to ds/R, by the definition of a
radian. At the point on the curve where s = ds, the tangent forms an
angle dθ (the same dθ) with the tangent at s = 0, so the rate of
change of theta as s increases is by definition dθ/ds.

Since dθ = ds/R, dθ/ds = 1/R, which is the curvature C, but it's

also the “Angular Velocity” of the tangent direction as a function
of s. It’s not really a “velocity” since time is not involved. In a
message I never posted (or I think I didn’t) I called it “telocity”,
thinking the use of “Velocity” might lead other people to make
Rick’s mistake. The “Angular Telocity” is another way of saying
“curvature”. I like “curvature” much better

Now what Alex measured was the true Angular Velocity of something

moving through time along the curve. we haven’t introduced time up
to this point, but we do now. He labelled Angular Velocity “A”. His
A was a function of time and distance, not of pure distance along
the curve. How fast θ changes as a function of time depends on how
fast the thing Alex was watching moves around the curve, which can
be symbolized as V = ds/dt. There’s no constraint on V. It can be
whatever the moving thing chooses.

There's a basic identity in calculus called the "chain rule". It

says that if you have dy/dx and you are interested in dy/dt instead,
dy/dt = (dy/dx)(dx/dt). This means we can write dθ/dt, which is
Alex’s “A”, as (dθ/ds)(ds/dt) or V/R where V is the linear velocity
along the curve. One can equally well write it as A = VC or V =
AR. Obviously, if V is constant, A is proportional to C – Angular
velocity is proportional to curvature if the linear velocity is
constant. There’s really no mystery about it at all.

I guess that's enough for now. There's no real need to go into all

the stuff with Rick’s “D” variable, which is just C/V³ ,
whatever V might happen to be at the point where C is measured. It’s
really irrelevant to the problem, which was that Alex wondered why
the quite freely chosen V should so often be a power function of R
(or equivalently, of C).

Martin

[Alex_Gomez-Marin]

I agree with Martin.

And without wanting to make “more wood out of the fallen tree” (Spanish idiom), let me say that it is absolutely amazing that an endless rephrasing of Powers’ insights is put forth automatically and ruthlessly in order to decide ex-cathedra that the subtle issue of the speed-curvature power-law phenomenon is an illusion when one does not even understand, from the very beginning, the very basic of the mater: C=1/R. Amazing to then claim that 40 years of a whole field of motor control is rubbish (aka, needs to go to the basket) not even understanding the relationship between radius of curvature and curvature. This is the sort of PCT-chauvinism that puts so many people off.

···

On Sun, Sep 4, 2016 at 11:59 PM, Martin Taylor mmt-csg@mmtaylor.net wrote:

[Martin Taylor 2016.09.04.16.00]

[From Rick Marken (2016.09.03.1455)]

      RM: Actually it was my wife and I who had dinner with Gary

Cziko and his lovely wife. …But the most important thing I
learned from our discussion was that as radius of curvature,
R, increases, curvature decreases! …

      RM: [There is still a problem for me with the fact that the

power relationship between curvature, measured as C (1/R), and
angular velocity, measured as A (V/R), still seems to show an
increase in velocity (A) with curvature (C) since larger
values of C now mean greater curvature and larger values of A
mean greater speed around a curve).

These are two rather shocking statements, considering that both of

the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months
that your analysis of the situation was the only correct one.

It seems that an introductory explanation is in order, simpler than

Bruce and I have offered before, when we (or at least I) believed
you understood these elementary fundamental facts about curvature.
It’s no wonder that our explanations rolled off like water off a
duck’s back! So here goes.

Curvature is _defined_ as 1/R where R is the radius of curvature of

what is called an “osculating circle”. What is an osculating circle?
It has a similar relation to the curve as does a tangent line.

The "curve" in this diagram is a parabola, but that's irrelevant to

the issues at hand. The figure shows an osculating circle for that
particular curve at the point we may call “s=0”. "s, then is the
distance along the curve from that point. It so happens that the
circle matches the parabola very closely for quite a long distance
away from the actual tangent point, a fact that might be relevant to
Alex’s problem.

At some small distance "ds" along the curve (the diagram shows ds as

a large distance, for clarity), the angle at the centre of the
circle between the radii that meet the circle at s=0 and at s=ds is
dθ. dθ in radians is exactly equal to ds/R, by the definition of a
radian. At the point on the curve where s = ds, the tangent forms an
angle dθ (the same dθ) with the tangent at s = 0, so the rate of
change of theta as s increases is by definition dθ/ds.

Since dθ = ds/R, dθ/ds = 1/R, which is the curvature C, but it's

also the “Angular Velocity” of the tangent direction as a function
of s. It’s not really a “velocity” since time is not involved. In a
message I never posted (or I think I didn’t) I called it “telocity”,
thinking the use of “Velocity” might lead other people to make
Rick’s mistake. The “Angular Telocity” is another way of saying
“curvature”. I like “curvature” much better

Now what Alex measured was the true Angular Velocity of something

moving through time along the curve. we haven’t introduced time up
to this point, but we do now. He labelled Angular Velocity “A”. His
A was a function of time and distance, not of pure distance along
the curve. How fast θ changes as a function of time depends on how
fast the thing Alex was watching moves around the curve, which can
be symbolized as V = ds/dt. There’s no constraint on V. It can be
whatever the moving thing chooses.

There's a basic identity in calculus called the "chain rule". It

says that if you have dy/dx and you are interested in dy/dt instead,
dy/dt = (dy/dx)(dx/dt). This means we can write dθ/dt, which is
Alex’s “A”, as (dθ/ds)(ds/dt) or V/R where V is the linear velocity
along the curve. One can equally well write it as A = VC or V =
AR. Obviously, if V is constant, A is proportional to C – Angular
velocity is proportional to curvature if the linear velocity is
constant. There’s really no mystery about it at all.

I guess that's enough for now. There's no real need to go into all

the stuff with Rick’s “D” variable, which is just C/V³ ,
whatever V might happen to be at the point where C is measured. It’s
really irrelevant to the problem, which was that Alex wondered why
the quite freely chosen V should so often be a power function of R
(or equivalently, of C).

Martin

[rsmarken]

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

RM: But the most important thing I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …
RM: [There is still a problem for me with the fact that the
power relationship between curvature, measured as C (1/R), and angular
velocity, measured as A (V/R), still seems to show an increase in velocity (A)
with curvature (C) since larger values of C now mean greater curvature and larger values of A mean greater speed around
a curve).

MT: These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months that your
analysis of the situation was the only correct one.

RM: Well, then you’ll be really shocked to know that I still think my analysis is correct. Your tutorial on what the variables R, V, C and A represent was very helpful but my analysis doesn’t depend on knowing, for example, that curvature increases as R decreases. Knowing this just helped me understand why you think that the power law shows that movement slows down through curves. And this helps me understand why you (and power law researchers) are so taken in by the illusion that the power law tells us something about how movement trajectories are produced; the power law is a quantitative representation of what we all think is true intuitively; we slow down through curves.

RM: My analysis is based on recognition of the fact that when you observe a movement trajectory you are looking at the (possibly controlled) result of an agents’ actions . (The fact that power law researchers never test to see whether the movement under study is actually a controlled result of action or not should have tipped you off right away that this research had little to contribute to our understanding of how organisms produce purposeful behavior – how they control). If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself. So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the combined result of the actions of the system and disturbances to that variable. So you can’t tell anything about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being produced – “looking at” it in terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. So a control theory analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced movement trajectories. Yet, power law researchers do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a 2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between these variables (and correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V = D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is |dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables that accounts for the variance in the criterion variable is omitted from the analysis.

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve. But my analysis shows that the power law finding has nothing to do with biology or physics. It is a statistical artifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two aspects of the movement will tell you nothing about how the movement is produced. But when the measures you use are R and V (or C and A) you will often see a power relationship between these variables (with a coefficient close to 1/3 or 2/4). But this is a statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

···

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[MartinT]

[Martin Taylor 2016.09.05.14.57]

[Martin Taylor 2016.09.05.15.01]

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

            RM: But the most important thing

I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …

            RM: [There is still a problem for

me with the fact that the
power relationship between curvature, measured as C
(1/R), and angular
velocity, measured as A (V/R), still seems to show an
increase in velocity (A)
with curvature (C) since larger values of C now mean
greater curvature and larger values of A mean greater
speed around
a curve).

                        MT:

These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical
in Alex’s
experiment, and yet you have been insisting for nearly two
months that your
analysis of the situation was the only correct one.

          RM: Well,

then you’ll be really shocked to know that I still think
my analysis is correct.

Shocked, yes; surprised, no.

Martin

[Alex_Gomez-Marin]

AGM: any evidence, be it A or not-A, shall always further confirm Rick’s claims, cause they were right regardless of any evidence… So now that I learned that the power law can only be an illusion and Rick learned some basic maths, can we move forward and find whence it comes?

···

On Monday, 5 September 2016, Martin Taylor mmt-csg@mmtaylor.net wrote:

[Martin Taylor 2016.09.05.14.57]

[Martin Taylor 2016.09.05.15.01]

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

            RM: But the most important thing

I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …

            RM: [There is still a problem for

me with the fact that the
power relationship between curvature, measured as C
(1/R), and angular
velocity, measured as A (V/R), still seems to show an
increase in velocity (A)
with curvature (C) since larger values of C now mean
greater curvature and larger values of A mean greater
speed around
a curve).

                        MT:

These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical
in Alex’s
experiment, and yet you have been insisting for nearly two
months that your
analysis of the situation was the only correct one.

          RM: Well,

then you’ll be really shocked to know that I still think
my analysis is correct.

Shocked, yes; surprised, no.



Martin

[Huddy_Vyv]

[Vyv Huddy (2211.05.09.2016)]

[From Rick Marken (2016.09.05.1045)]

RM: If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself.

VH: What are the disturbances referred to here? I looked at the spreadsheet model and couldn’t find these? Perhaps I misunderstanding what’s included there but I thought it was the
PCT model in the figure? In the figure the disturbances are environmental but if someone is drawing on a flat stable surface then I’m not sure what they might be?

VH: I can understand a distrubance be at higher levels perception, like a reference to perceive elipse configuration might be disturbed by a blank piece of paper I think?? If the instruction
is to draw an elipse?

So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the
combined result of the actions of the system and disturbances to that variable. So you can’t tell anything
about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being
produced – “looking at” it in
terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful
movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. ** So a control theory analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced
movement trajectories.** Yet, power law researchers
do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a
2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found
for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law
research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature
and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between
these variables (and correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the
relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature
and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V = D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is |dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the
criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables
that accounts for the variance in the criterion variable is omitted from the analysis.

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is
based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance
in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve.
But my analysis shows that the power law finding has nothing to do with biology or physics. It is a statistical artifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that
contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it
is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two
aspects of the movement will tell you nothing about how the movement is produced. But when the measures you use are R and V (or C and A) you will often see a power relationship between these variables (with a coefficient close to 1/3 or 2/4). But this is a
statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation
of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

···

–

Richard S. Marken

“The childhood of the human race is far from over. We have a long way to go before most people will understand that what they do for others is just as important to their well-being as what they do for themselves.”
– William T. Powers

[rsmarken]

[From RIck Marken (2016.09.05.1850)]

···

Vyv Huddy (2211.05.09.2016)–

RM: If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself.

VH: What are the disturbances referred to here? I looked at the spreadsheet model and couldn’t find these? Perhaps I misunderstanding what’s included there but I thought it was the
PCT model in the figure? In the figure the disturbances are environmental but if someone is drawing on a flat stable surface then I’m not sure what they might be?

RM: Disturbances are variations in environmental variables that affect controlled variables independently of the effect that the system has on these variables. When you are drawing (or writing) on a flat, stable surface the controlled variable is the X, Y position of the pen tip. Disturbances to that variable are things like variations in the texture of the paper, in the wetness of the pen tip, in the the push-down force you are exerting on the pen; variations in any physical variables that affect the movement of the pen across the paper. In the spreadsheet model the disturbances are the variables dx and dy, which affect the position of the cursor (variables X and Y) for both the person and the model.

RM: All behavior is produced in a disturbance prone world. A causal model can’t behave in such a world like an organism does. PCT is the only model that can behave like an organism does in the real world of unpredictable (and typically invisible) disturbances. It does this, of course, by controlling its inputs rather than its outputs.

Best

Rick

VH: I can understand a distrubance be at higher levels perception, like a reference to perceive elipse configuration might be disturbed by a blank piece of paper I think?? If the instruction
is to draw an elipse?

So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the
combined result of the actions of the system and disturbances to that variable. So you can’t tell anything
about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being
produced – “looking at” it in
terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful
movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. ** So a control theory analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced
movement trajectories.** Yet, power law researchers
do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a
2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found
for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law
research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature
and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between
these variables (and correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the
relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature
and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V = D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is |dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the
criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables
that accounts for the variance in the criterion variable is omitted from the analysis.

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is
based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance
in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve.
But my analysis shows that the power law finding has nothing to do with biology or physics. It is a statistical artifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that
contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it
is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two
aspects of the movement will tell you nothing about how the movement is produced. But when the measures you use are R and V (or C and A) you will often see a power relationship between these variables (with a coefficient close to 1/3 or 2/4). But this is a
statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation
of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

–

Richard S. Marken

“The childhood of the human race is far from over. We have a long way to go before most people will understand that what they do for others is just as important to their well-being as what they do for themselves.”
– William T. Powers

–

Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[wmansell]

Rick, I agree with you right up to the bit where you think the relationship must be an artefact of mathematics. One can find relationships between variables for reasons other than this (physical, biological) without questioning your first assertion that the power law tells us nothing about how the movements are produced. I don’t think Alex wants us to believe this anyway. It can work the other way round - a PCT model can show how a power law relationship emerges just as it can show how an apparent stimulus-response relationship emerges, despite the PCT model making it clear it is nothing of the sort, but actually a disturbance-output relationship within a closed loop that would not exist without the closed loop.

Warren

···

On 5 Sep 2016, at 18:47, Richard Marken < rsmarken@ gmail.com> wrote:

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

RM: But the most important thing I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …
RM: [There is still a problem for me with the fact that the
power relationship between curvature, measured as C (1/R), and angular
velocity, measured as A (V/R), still seems to show an increase in velocity (A)
with curvature (C) since larger values of C now mean greater curvature and larger values of A mean greater speed around
a curve).

MT: These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months that your
analysis of the situation was the only correct one.

RM: Well, then you’ll be really shocked to know that I still think my analysis is correct. Your tutorial on what the variables R, V, C and A represent was very helpful but my analysis doesn’t depend on knowing, for example, that curvature increases as R decreases. Knowing this just helped me understand why you think that the power law shows that movement slows down through curves. And this helps me understand why you (and power law researchers) are so taken in by the illusion that the power law tells us something about how movement trajectories are produced; the power law is a quantitative representation of what we all think is true intuitively; we slow down through curves.

RM: My analysis is based on recognition of the fac
t that when you observe a movement trajectory you are looking at the (possibly controlled) result of an agents’ actions . (The fact that power law researchers never test to see whether the movement under study is actually a controlled result of action or not should have tipped you off right away that this research had little to contribute to our understanding of how organisms produce purposeful behavior – how they control). If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself. So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the combined result of the actions of the system and disturbances to that variable. So you can’t tell anything about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being produced – “looking at” it in terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. ** So a control theo
ry analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced movement trajectories.** Yet, power law researchers do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a 2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between these variables (and
correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V = D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is |dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables that accounts for t
he variance in the criterion variable is omitted from the analysis.

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve. But my analysis shows that the power law
finding has nothing to do with biology or physics. It is a statistical artifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two aspects of the movement will tell you nothing about how the movement is produced. But when the meas
ures you use are R and V (or C and A) you will often see a power relationship between these variables (with a coefficient close to 1/3 or 2/4). But this is a statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[MartinT]

[Martin Taylor 2016.09.06.09.10]

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

            RM: But the most important thing

I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …

            RM: [There is still a problem for

me with the fact that the
power relationship between curvature, measured as C
(1/R), and angular
velocity, measured as A (V/R), still seems to show an
increase in velocity (A)
with curvature (C) since larger values of C now mean
greater curvature and larger values of A mean greater
speed around
a curve).

                        MT:

These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical
in Alex’s
experiment, and yet you have been insisting for nearly two
months that your
analysis of the situation was the only correct one.

          RM: Well,

then you’ll be really shocked to know that I still think
my analysis is correct…

I have never complained about the correctness of your mathematics

that produced the tautology V=V. So far as I can see, it is
perfectly correct, and the result is plausible.

Most long disputes are based in some kind of misunderstanding, and I

wonder if this one might be another example. I think I know what you
are claiming that I have been saying is wrong – to me it has seemed
pretty clear, but I could have been wrong all this time. If we could
be more sure we aren’t talking at cross-purposes, there might be a
path forward to an agreement. It might be helpful if you could say
in four lines or less of non-mathematical text just what it is that
you think you are right about, because I’m pretty sure it isn’t that
V=V.

No maths, just a short and clear statement of claim, please.

Martin

[Alex_Gomez-Marin]

i think rick’s statement so far isn’t more than what he would have said before even knowing that the speed-curvature relation existed in humans and flies: the any invariant between output degrees of freedom is not behavior.

now, the question is: from what behavior does that invariant come from?

so, 2 months after my initial email, we are back to where we started (V=V and output=illusion). time to kick ass in the motor control literature with some juicy perceptual control insights…!!!

···

On Tuesday, 6 September 2016, Martin Taylor mmt-csg@mmtaylor.net wrote:

[Martin Taylor 2016.09.06.09.10]

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

            RM: But the most important thing

I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …

            RM: [There is still a problem for

me with the fact that the
power relationship between curvature, measured as C
(1/R), and angular
velocity, measured as A (V/R), still seems to show an
increase in velocity (A)
with curvature (C) since larger values of C now mean
greater curvature and larger values of A mean greater
speed around
a curve).

                        MT:

These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical
in Alex’s
experiment, and yet you have been insisting for nearly two
months that your
analysis of the situation was the only correct one.

          RM: Well,

then you’ll be really shocked to know that I still think
my analysis is correct…

I have never complained about the correctness of your mathematics

that produced the tautology V=V. So far as I can see, it is
perfectly correct, and the result is plausible.

Most long disputes are based in some kind of misunderstanding, and I

wonder if this one might be another example. I think I know what you
are claiming that I have been saying is wrong – to me it has seemed
pretty clear, but I could have been wrong all this time. If we could
be more sure we aren’t talking at cross-purposes, there might be a
path forward to an agreement. It might be helpful if you could say
in four lines or less of non-mathematical text just what it is that
you think you are right about, because I’m pretty sure it isn’t that
V=V.

No maths, just a short and clear statement of claim, please.



Martin

[FredNickols]

[From Fred Nickols (2016.09.06.1632 ET)]

Alex:

I’ll echo Martin’s request. Would you please start putting a date-stamp on your posts to the list? That’s a key feature of this list and it enables searching and reconstructing threads.

Fred Nickols

···

From: Alex Gomez-Marin [mailto:agomezmarin@gmail.com]
Sent: Tuesday, September 06, 2016 12:36 PM
To: csgnet@lists.illinois.edu
Subject: Re: My Dinner with Andre

i think rick’s statement so far isn’t more than what he would have said before even knowing that the speed-curvature relation existed in humans and flies: the any invariant between output degrees of freedom is not behavior.

now, the question is: from what behavior does that invariant come from?

so, 2 months after my initial email, we are back to where we started (V=V and output=illusion). time to kick ass in the motor control literature with some juicy perceptual control insights…!!!

On Tuesday, 6 September 2016, Martin Taylor mmt-csg@mmtaylor.net wrote:

[Martin Taylor 2016.09.06.09.10]

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

RM: But the most important thing I learned from our discussion was that as radius of curvature, R, increases, curvature decreases! …

RM: [There is still a problem for me with the fact that the power relationship between curvature, measured as C (1/R), and angular velocity, measured as A (V/R), still seems to show an increase in velocity (A) with curvature (C) since larger values of C now mean greater curvature and larger values of A mean greater speed around a curve).

MT: These are two rather shocking statements, considering that both of the things you didn’t know are absolutely critical in Alex’s experiment, and yet you have been insisting for nearly two months that your analysis of the situation was the only correct one.

RM: Well, then you’ll be really shocked to know that I still think my analysis is correct…

I have never complained about the correctness of your mathematics that produced the tautology V=V. So far as I can see, it is perfectly correct, and the result is plausible.

Most long disputes are based in some kind of misunderstanding, and I wonder if this one might be another example. I think I know what you are claiming that I have been saying is wrong – to me it has seemed pretty clear, but I could have been wrong all this time. If we could be more sure we aren’t talking at cross-purposes, there might be a path forward to an agreement. It might be helpful if you could say in four lines or less of non-mathematical text just what it is that you think you are right about, because I’m pretty sure it isn’t that V=V.

No maths, just a short and clear statement of claim, please.

Martin

[rsmarken]

[From Rick Marken (2016.09.06.1445)]

···

On Tue, Sep 6, 2016 at 4:11 AM, Warren Mansell wmansell@gmail.com wrote:

WM: Rick, I agree with you right up to the bit where you think the relationship must be an artefact of mathematics.

RM: Gee, that’s the best bit!

WM: One can find relationships between variables for reasons other than this (physical, biological) without questioning your first assertion that the power law tells us nothing about how the movements are produced. I don’t think Alex wants us to believe this anyway.

RM: I don’t understand. What does Alex not want us to believe?

WM: It can work the other way round - a PCT model can show how a power law relationship emerges just as it can show how an apparent stimulus-response relationship emerges,

RM: But that’s what I have shown, though the PCT model shows that the power law doesn’t “emerge” in the same way as the stimulus-response illusion. It emerges from thinking that what we would call disturbance and output are visible in the behavior of a controlled variable (the observed movement trajectory).

WM: despite the PCT model making it clear it is nothing of the sort, but actually a disturbance-output relationship within a closed loop that would not exist without the closed loop.

RM: Yes, but in this case the measures of curvature and velocity are not measures of disturbance and output.

RM: Your question made me realize that there is a way to test my PCT explanation of the power law! The PCT analysis shows that the observed power relationship between curvature and velocity is completely determined by the nature of the movement trajectory itself. So according to this analysis, the reason power law researchers typically find power coefficients of approximately 1/3 or 2/3 (and occasionally of approximately 1/4 and 3/4) is because the movement trajectories they’ve observed in their studies are one’s that will yield estimates of the power coefficient that are close to those values when log curvature is regressed on log velocity. And from my experience most curvy movement trajectories yield power coefficients close to 1/3 and 2/3. But I have been able to generate trajectories that yield power coefficients that deviate considerably from 1/3 and 2/3 (such as -1/2). I predict that if I use these trajectories as target tracks in a pursuit tracking task, the movement trajectory made by the person doing the tracking will yield power coefficients that deviate considerably from the 1/3 and 2/3 values typically found in power law research. Such a result would show that the power law does not reflect a constraint on movement production. If I don’t get that result – if the power law estimate is still close to 1/3 or 2/3 – then the power law researchers have, indeed, discovered a real constraint on movement;-)

Best

Rick

On 5 Sep 2016, at 18:47, Richard Marken rsmarken@gmail.com wrote:

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

RM: But the most important thing I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …
RM: [There is still a problem for me with the fact that the
power relationship between curvature, measured as C (1/R), and angular
velocity, measured as A (V/R), still seems to show an increase in velocity (A)
with curvature (C) since larger values of C now mean greater curvature and larger values of A mean greater speed around
a curve).

MT: These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months that your
analysis of the situation was the only correct one.

RM: Well, then you’ll be really shocked to know that I still think my analysis is correct. Your tutorial on what the variables R, V, C and A represent was very helpful but my analysis doesn’t depend on knowing, for example, that curvature increases as R decreases. Knowing this just helped me understand why you think that the power law shows that movement slows down through curves. And this helps me understand why you (and power law researchers) are so taken in by the illusion that the power law tells us something about how movement trajectories are produced; the power law is a quantitative representation of what we all think is true intuitively; we slow down through curves.

RM: My analysis is based on recognition of the fact that when you observe a movement trajectory you are looking at the (possibly controlled) result of an agents’ actions . (The fact that power law researchers never test to see whether the movement under study is actually a controlled result of action or not should have tipped you off right away that this research had little to contribute to our understanding of how organisms produce purposeful behavior – how they control). If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself. So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the combined result of the actions of the system and disturbances to that variable. So you can’t tell anything about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being produced – “looking at” it in terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. So a control theory analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced movement trajectories. Yet, power law researchers do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a 2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between these variables (and correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V = D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is |dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables that accounts for the variance in the criterion variable is omitted from the analysis.

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve. But my analysis shows that the power law finding has nothing to do with biology or physics. It is a statistical artifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two aspects of the movement will tell you nothing about how the movement is produced. But when the measures you use are R and V (or C and A) you will often see a power relationship between these variables (with a coefficient close to 1/3 or 2/4). But this is a statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[wmansell]

Hi Rick, I predict you will find that result, to the degree that the traces are accurate measures of the reference trace, but that still doesn’t explain why your traces flout the law. They flout the law because you are a complex, wise perceptual control system who is actively challenging the tendency for biophysiological constraints to make you conform with the law. You are using CVs other than the ones typically used by animals and humans that normally entail that the ‘slowing down at curves’ typically gets you the higher level goals you want (possibly energy conservation; highest mean on track velocity along the path; highest accuracy of trace - just hypotheses). If you do a TCV on yourself as you generate the anomalous traces, there is one PCT model, and the other is the power law-conforming default. If a study compares the two models and
gets the contrast, there is the result that PCT can contribute.

RSVP,

Warren

···

On Tue, Sep 6, 2016 at 4:11 AM, Warren Mansell wmansell@gmail.com wrote:

WM: Rick, I agree with you right up to the bit where you think the relationship must be an artefact of mathematics.

RM: Gee, that’s the best bit!

WM: One can find relationships between variables for reasons other than this (physical, biological) without questioning your first assertion that the power law tells us nothing about how the movements are produced. I don’t think Alex wants us to believe this anyway.

RM: I don’t understand. What does Alex not want us to believe?

WM: It can work the other way round - a PCT model can show how a power law relationship emerges just as it can show how an apparent stimulus-response relationship emerges,

RM: But that’s what I have shown, though the PCT model shows that the power law doesn’t “emerge” in the same way as the stimulus-response illusion. It emerges from thinking that what we would call disturbance and output are visible in the behavior of a controlled variable (the observed movement trajectory).

WM: despite the PCT model making it clear it is nothing of the sort, but actually a disturbance-output relationship within a closed loop that would not exist without the closed loop.

RM: Yes, but in this case the measures of curvature and velocity are not measures of disturbance and output.

RM: Your question made me realize that there is a way to test my PCT explanation of the power law! The PCT analysis shows that the observed power relationship between curvature and velocity is completely determined by the nature of the movement trajectory itself. So according to this analysis, the reason power law researchers typic
ally find power coefficients of approximately 1/3 or 2/3 (and occasionally of approximately 1/4 and 3/4) is because the movement trajectories they’ve observed in their studies are one’s that will yield estimates of the power coefficient that are close to those values when log curvature is regressed on log velocity. And from my experience most curvy movement trajectories yield power coefficients close to 1/3 and 2/3. But I have been able to generate trajectories that yield power coefficients that deviate considerably from 1/3 and 2/3 (such as -1/2). I predict that if I use these trajectories as target tracks in a pursuit tracking task, the movement trajectory made by the person doing the tracking will yield power coefficients that deviate considerably from the 1/3 and 2/3 values typically found in power law research. Such a result would show that the power law does not reflect a constraint on movement production. If I don’t get that result – if the power law estimate i
s still close to 1/3 or 2/3 – then the power law researchers have, indeed, discovered a real constraint on movement;-)

Best

Rick

On 5 Sep 2016, at 18:47, Richard Marken rsmarken@gmail.com wrote:

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

RM: But the most important thing I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …
RM: [There is still a problem for me with the fact that the
power relationship between curvature, measured as C (1/R), and angular
velocity, measured as A (V/R), still seems to show an increase in velocity (A)
with curvature (C) since larger values of C now mean greater curvature and larger values of A mean greater speed around
a curve).

MT: These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months that your
analysis of the situation was the only correct one.

RM: Well, then you’ll be really shocked to know that I still think my analysis is correct. Your tutorial on what the variables R, V, C and A represent was very helpful but my analysis doesn’t depend on knowing, for example, that curvature increases as R decreases. Knowing this just helped me understand why you think that the power law shows that movement slows down through curves. And this helps me understand why you (and power law researchers) are so taken in by the illusion that the power law tells us something about how movement trajectories are produced; the power law is a quantitative representation of what we all think is true intuitively; we slow down through curves.

RM: My analysis is based on recognition of the fac
t that when you observe a movement trajectory you are looking at the (possibly controlled) result of an agents’ actions . (The fact that power law researchers never test to see whether the movement under study is actually a controlled result of action or not should have tipped you off right away that this research had little to contribute to our understanding of how organisms produce purposeful behavior – how they control). If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself. So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the combined result of the actions of the system and disturbances to that variable. So you can’t tell anything about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being produced – “looking at” it in terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. ** So a control theo
ry analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced movement trajectories.** Yet, power law researchers do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a 2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between these variables (and
correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V =
D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is <
span style=“font-size:10pt;line-height:15.3333px”>|dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables that accounts for the variance in the criterion variable is omitted from the analysis. <
/span>

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve. But my analysis shows that the power law finding has nothing to do with biology or physics. It is a statistical ar
tifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two aspects of the movement will tell you nothing about how the movement is produced. But when the measures you use are R and V (or C and A) you will often see a power relations
hip between these variables (with a coefficient close to 1/3 or 2/4). But this is a statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[rsmarken]

[From Rick Marken (2016.09.07.1040)]

···

On Tue, Sep 6, 2016 at 10:32 PM, Warren Mansell wmansell@gmail.com wrote:

WM: Hi Rick, I predict you will find that result, to the degree that the traces are accurate measures of the reference trace, but that still doesn’t explain why your traces flout the law.

RM: No, it would simply show that there is no law. We already know that the “law”, in terms of the power coefficient and R^2 value of the best fitting regression equation, differs depending on the nature of the movement trajectory being analyzed.

WM: They flout the law because you are a complex, wise perceptual control system who is actively challenging the tendency for biophysiological constraints to make you conform with the law.

RM: So doing this experiment would be a waste of time. Can you propose anothe way to test my explanation of the power law?

WM: You are using CVs other than the ones typically used by animals and humans

that normally entail that the ‘slowing down at curves’ typically gets you the higher level goals you want (possibly energy conservation; highest mean on track velocity along the path; highest accuracy of trace - just hypotheses).

RM: I don’t agree with your proposed CVs but I agree that I am controlling different variables when I do pursuit tracking (where I control the distance from target to cursor) versus when I am producing the same pattern from memory (where I control the optical position of the cursor in visual space). But I would design the experiment so that it uses only pursuit tracking with targets that are predictably consistent or inconsistent with the power law and show whether or not the power law is found depends on the movements of the target and has nothing to dowith how they are generated.

WM: If you do a TCV on yourself as you generate the anomalous traces, there is one PCT model, and the other is the power law-conforming default. If a study compares the two models and
gets the contrast, there is the result that PCT can contribute.

RM: I have no idea what this means, but I will use just one PCT model – the one that controls for keeping a cursor (t) aligned with a moving target (t) so that the CV is always t - c. And I predict that both the model and the human will make movements consistent with the power law for target movements consistent with the power law (like the an ellipse) and that are not consistent with the power law for target movements that are inconsistent with the power law.

Best

Rick

RSVP,

Warren

On 6 Sep 2016, at 22:48, Richard Marken rsmarken@gmail.com wrote:

[From Rick Marken (2016.09.06.1445)]

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

On Tue, Sep 6, 2016 at 4:11 AM, Warren Mansell wmansell@gmail.com wrote:

WM: Rick, I agree with you right up to the bit where you think the relationship must be an artefact of mathematics.

RM: Gee, that’s the best bit!

WM: One can find relationships between variables for reasons other than this (physical, biological) without questioning your first assertion that the power law tells us nothing about how the movements are produced. I don’t think Alex wants us to believe this anyway.

RM: I don’t understand. What does Alex not want us to believe?

WM: It can work the other way round - a PCT model can show how a power law relationship emerges just as it can show how an apparent stimulus-response relationship emerges,

RM: But that’s what I have shown, though the PCT model shows that the power law doesn’t “emerge” in the same way as the stimulus-response illusion. It emerges from thinking that what we would call disturbance and output are visible in the behavior of a controlled variable (the observed movement trajectory).

WM: despite the PCT model making it clear it is nothing of the sort, but actually a disturbance-output relationship within a closed loop that would not exist without the closed loop.

RM: Yes, but in this case the measures of curvature and velocity are not measures of disturbance and output.

RM: Your question made me realize that there is a way to test my PCT explanation of the power law! The PCT analysis shows that the observed power relationship between curvature and velocity is completely determined by the nature of the movement trajectory itself. So according to this analysis, the reason power law researchers typic
ally find power coefficients of approximately 1/3 or 2/3 (and occasionally of approximately 1/4 and 3/4) is because the movement trajectories they’ve observed in their studies are one’s that will yield estimates of the power coefficient that are close to those values when log curvature is regressed on log velocity. And from my experience most curvy movement trajectories yield power coefficients close to 1/3 and 2/3. But I have been able to generate trajectories that yield power coefficients that deviate considerably from 1/3 and 2/3 (such as -1/2). I predict that if I use these trajectories as target tracks in a pursuit tracking task, the movement trajectory made by the person doing the tracking will yield power coefficients that deviate considerably from the 1/3 and 2/3 values typically found in power law research. Such a result would show that the power law does not reflect a constraint on movement production. If I don’t get that result – if the power law estimate i
s still close to 1/3 or 2/3 – then the power law researchers have, indeed, discovered a real constraint on movement;-)

Best

Rick

On 5 Sep 2016, at 18:47, Richard Marken rsmarken@gmail.com wrote:

[From Rick Marken (2016.09.05.1045)]

Martin Taylor (2016.09.04.16.00) –

RM: But the most important thing I learned from our
discussion was that as radius of curvature, R,
increases, curvature decreases! …
RM: [There is still a problem for me with the fact that the
power relationship between curvature, measured as C (1/R), and angular
velocity, measured as A (V/R), still seems to show an increase in velocity (A)
with curvature (C) since larger values of C now mean greater curvature and larger values of A mean greater speed around
a curve).

MT: These are two rather shocking statements, considering that
both of the things you didn’t know are absolutely critical in Alex’s
experiment, and yet you have been insisting for nearly two months that your
analysis of the situation was the only correct one.

RM: Well, then you’ll be really shocked to know that I still think my analysis is correct. Your tutorial on what the variables R, V, C and A represent was very helpful but my analysis doesn’t depend on knowing, for example, that curvature increases as R decreases. Knowing this just helped me understand why you think that the power law shows that movement slows down through curves. And this helps me understand why you (and power law researchers) are so taken in by the illusion that the power law tells us something about how movement trajectories are produced; the power law is a quantitative representation of what we all think is true intuitively; we slow down through curves.

RM: My analysis is based on recognition of the fac
t that when you observe a movement trajectory you are looking at the (possibly controlled) result of an agents’ actions . (The fact that power law researchers never test to see whether the movement under study is actually a controlled result of action or not should have tipped you off right away that this research had little to contribute to our understanding of how organisms produce purposeful behavior – how they control). If the movement is purposeful then, due to disturbances, the actions that produce the observed movement trajectory will be quite different than the movement itself. So what you are looking at when you see a movement trajectory (if it is intentionally produced) is variations in a variable that are the combined result of the actions of the system and disturbances to that variable. So you can’t tell anything about the actions that produced the movement by just looking at the movement itself.

RM: It was this understanding about the nature of control that led to my mathematical analysis of the power law. Power law researchers are “looking at” only the movement that is being produced – “looking at” it in terms of measures of curvature and velocity – and thinking that one measure is an independent variable (curvature) and the other a dependent variable (velocity). But according to control theory the independent and dependent variables that result in a purposeful movement trajectories (disturbance and output) are not visible in the movement trajectories themselves. ** So a control theo
ry analysis would lead one to expect that there would be no relationship at all between any two measures of intentionally produced movement trajectories.** Yet, power law researchers do observe a fairly regular relationship between measures of curvature and velocity in many movement trajectories; the relationship is a 1/3 power law when curvature and velocity are measured as R and V, respectively, and a 2/3 power law when curvature and velocity are measured as C and A, respectively.

RM: It was this surprising fact – that a nice power law relationship was found where control theory says it should not be found (as well as the fact that this power law is also found for unintentionally produced movement trajectories, like the movements of the planets) – that led me to suspect that the power law might be a mathematical property of the relationship between the measures of curvature and velocity that are used in power law research. After all, the power law is found using regression analysis with measures of curvature as the predictor variable and measures of velocity as the criterion variable in the analysis. If there is a mathematical relationship between the measures of curvature and velocity used in power law research the regression analysis will pick this up.

RM: So I looked at the equations for computing the values of R (curvature) and V (velocity) in power law research and discovered that there was indeed a mathematical relationship between these variables (and
correspondingly between curvature measured as C and velocity measured as A). And the mathematical relationship is a power relationship with a 1/3 power coefficient for the relationship between R and V and a 2/3 power coefficient for the relationship between C and A, exactly the values that power law researchers have been finding for many movement trajectories. Coincidence? I didn’t think so. But power law researchers don’t always find a 1/3 or 2/3 power law relationship between curvature and velocity. That was kind of a challenge until I realized that the mathematical relationship between measures of R and V (and between C and A) contains another variable, D, so that the complete formula relating R to V is:

V =
D^1/3 *R^1/3

and C to A is

A = D^1/3 *C2^/3

where is is <
span style=“font-size:10pt;line-height:15.3333px”>|dXd²Y-d²XdY|.

RM: So I realized that if one does a log-log regression of R on V (or of C on A) the value of the coefficient that is found by the analysis will depend on how much of the variance in the criterion variable is due to the variable left out of the analysis, D. That is, the value of the estimate of the power coefficient that is found by regression analysis will be biased from its true value (1/3 or 2/3, per the equations above) if one of the variables that accounts for the variance in the criterion variable is omitted from the analysis. <
/span>

RM: So, as you can see, my analysis of the power law has nothing to do with what the measures of curvature and velocity – R, V, C and A – measure about the trajectory. My analysis is based only on treating R, V, C and A as variables, as is done in power law research. In that research, regression analysis is used to determine how much of the variance in V (or A) can be accounted for by variance in R (or C). They find that the most variance in V (or A) is usually best accounted for by a 1/3 (or 2/3) power function of R (or C). They take this finding to mean that there is a biophysical constraint on the relationship between the curvature and the speed with which movement occurs through that curve. But my analysis shows that the power law finding has nothing to do with biology or physics. It is a statistical ar
tifact; a result of failure to include in the statistical (regression) analysis used to determine the power law one of the variables (D) that contributes to the variance in the criterion variable (V or A).

RM: So explaining what the variables R, V, C and A measure is not really relevant to this analysis, nor does it disprove the analysis. The analysis is based on the observation that it is impossible to extract information about how purposeful movement trajectories are produced by measuring only properties of the movement trajectory itself. So it doesn’t matter what aspects of the movement trajectories are measured – measures of any two aspects of the movement will tell you nothing about how the movement is produced. But when the measures you use are R and V (or C and A) you will often see a power relations
hip between these variables (with a coefficient close to 1/3 or 2/4). But this is a statistical artifact – an illusion in the sense that the observed relationship does not show what it seems to show – how organisms vary the speed with which they go through curves. Organisms do vary the speed with which they go through curves, but the explanation of how they do this is control theory, not biophyisical constraints, as suggested by the power law.

Best regards

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[MartinT]

[Martin Taylor 2016.09.07.15.39]

[From Rick Marken (2016.09.07.1040)]

I asked you [Martin Taylor 2016.09.06.09.10] if you would mind

providing a short form explanation of what you claim about the power
law. When I asked the question I thought I understood, but following
your two messages to Warren, I find I don’t understand at all. So
could you just give a quick, non-mathematical description of what
actually IS your explanation of the power law?

Martin

···

On Tue, Sep 6, 2016 at 10:32 PM,
Warren Mansell wmansell@gmail.com wrote:

                WM: Hi Rick, I predict you will find that result,

to the degree that the traces are accurate measures
of the reference trace, but that still doesn’t
explain why your traces flout the law.

          RM: No, it would simply show that there is no law. We

already know that the “law”, in terms of the power
coefficient and R^2 value of the best fitting regression
equation, differs depending on the nature of the movement
trajectory being analyzed.

                WM: They flout the law because you are a complex,

wise perceptual control system who is actively
challenging the tendency for biophysiological
constraints to make you conform with the law.

          RM:  So doing this experiment would be a waste of time.

Can you propose anothe way to test my explanation of the
power law?

[Huddy_Vyv]

[Martin Taylor 2016.09.07.15.39]

So could you just give a quick, non-mathematical description of what actually IS your explanation of the power law?

[Vyv Huddy 2117.7.09.216]
I'd also be very grateful of a non-mathematical description. Thanks.
Martin

[rsmarken]

[From Rick Marken (2016.09.07.1420)]

Martin Taylor (2016.09.07.15.39)--

MT: I asked you [Martin Taylor 2016.09.06.09.10] if you would mind providing a short form explanation of what you claim about the power law. When I asked the question I thought I understood, but following your two messages to Warren, I find I don't understand at all. So could you just give a quick, non-mathematical description of what actually IS your explanation of the power law?

RM: Yes, I think it's a good idea. I was trying to compose it but got waylaid. So here we go again:
RM: The first step in the study of how organisms produce movement trajectories should be the determination of whether or not the trajectories that are observed are purposefully produced -- whether or not the movement trajectory or some aspect thereof is a controlled variable. This is very important because physics already has a very good explanation of non-purposefully produced movement trajectories, like those of the planets. So my analysis assumes that the movement trajectories under study are purposefully produced results of an organisms outputs.
RM: Assuming movement trajectories are controlled results of action then power law researchers are measuring two aspects of a controlled variable --its instantaneous curvature and velocity throughout the course of the movement. These two measures of the movement trajectory are presumed to represent variables involved in the production (which in PCT we take to mean control) of the movement. But we know from PCT that it is impossible to see the variables involved in keeping a controlled variable under control by simply observing the behavior of the controlled variable itself.
RM: So the observation of a fairly regular relationship between different measures of a controlled variable (in this case the "power law" relationship between curvature and velocity measures) must be due to something other than a relationship between the variable involved in producing the movement. It turns out that there is a mathematical relationship between the different measures of the controlled variable -- curvature and velocity-- that perfectly accounts for the "power law" relationship between these variables that is observed in studies of movement trajectories.
RM: That's not that quick, I'm afraid. But it's the best I can do for now. I'll try to hone it down as I continue to work on it. But I will say that there is a positive implication of this analysis: if you want to understand how people produce purposeful movement, stop asking what the power law suggests about how these movements are produced and start asking what variables are being controlled when people produce these movements. We know the movement is being controlled but that's pretty general. It should be possible to develop experiments to test whether the velocity of the movement, or the curvature or both are being controlled. Or something else about the movement? And how is this control achieved.
RM: In other words, don't go chasing illusions; study he real thing -- study the fact of control.
Best
Rick

···

--
Richard S. Marken
"The childhood of the human race is far from over. We have a long way to go before most people will understand that what they do for others is just as important to their well-being as what they do for themselves." -- William T. Powers

[Alex_Gomez-Marin]

[From Alex Gomez-Marin (2016.09.07.1134)]

​​

​​

​AGM: Rick, I really really liked what you say in the last email until you jump from a conscious and clear explanation onto an ad hoc statement which is false: “It turns out that there is a mathematical relationship between the different measures of the controlled variable – curvature and velocity-- that perfectly accounts for the “power law” relationship between these variables that is observed in studies of movement trajectories.
​” FALSE FALSE FALSE! But you don’t care.

···

On Wed, Sep 7, 2016 at 11:18 PM, Richard Marken rsmarken@gmail.com wrote:

[From Rick Marken (2016.09.07.1420)]

Martin Taylor (2016.09.07.15.39)–

MT: I asked you [Martin Taylor 2016.09.06.09.10] if you would mind

providing a short form explanation of what you claim about the power
law. When I asked the question I thought I understood, but following
your two messages to Warren, I find I don’t understand at all. So
could you just give a quick, non-mathematical description of what
actually IS your explanation of the power law?

RM: Yes, I think it’s a good idea. I was trying to compose it but got waylaid. So here we go again:

RM: The first step in the study of how organisms produce movement trajectories should be the determination of whether or not the trajectories that are observed are purposefully produced – whether or not the movement trajectory or some aspect thereof is a controlled variable. This is very important because physics already has a very good explanation of non-purposefully produced movement trajectories, like those of the planets. So my analysis assumes that the movement trajectories under study are purposefully produced results of an organisms outputs.

RM: Assuming movement trajectories are controlled results of action then power law researchers are measuring two aspects of a controlled variable --its instantaneous curvature and velocity throughout the course of the movement. These two measures of the movement trajectory are presumed to represent variables involved in the production (which in PCT we take to mean control) of the movement. But we know from PCT that it is impossible to see the variables involved in keeping a controlled variable under control by simply observing the behavior of the controlled variable itself.

RM: So the observation of a fairly regular relationship between different measures of a controlled variable (in this case the “power law” relationship between curvature and velocity measures) must be due to something other than a relationship between the variable involved in producing the movement. It turns out that there is a mathematical relationship between the different measures of the controlled variable – curvature and velocity-- that perfectly accounts for the “power law” relationship between these variables that is observed in studies of movement trajectories.

RM: That’s not that quick, I’m afraid. But it’s the best I can do for now. I’ll try to hone it down as I continue to work on it. But I will say that there is a positive implication of this analysis: if you want to understand how people produce purposeful movement, stop asking what the power law suggests about how these movements are produced and start asking what variables are being controlled when people produce these movements. We know the movement is being controlled but that’s pretty general. It should be possible to develop experiments to test whether the velocity of the movement, or the curvature or both are being controlled. Or something else about the movement? And how is this control achieved.

RM: In other words, don’t go chasing illusions; study he real thing – study the fact of control.

Best

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

[rsmarken]

[From Rick Marken (2016.09.07.1710)]

···

Alex Gomez-Marin (2016.09.07.1134)

​​

​​

​AGM: Rick, I really really liked what you say in the last email until you jump from a conscious and clear explanation onto an ad hoc statement which is false: “It turns out that there is a mathematical relationship between the different measures of the controlled variable – curvature and velocity-- that perfectly accounts for the “power law” relationship between these variables that is observed in studies of movement trajectories.
​” FALSE FALSE FALSE! But you don’t care.

RM: I do care. But no one has shown me that what I’ve found is false. I would be grateful if you would try to show me again why my derivation is false. Again, I assume these are the formulae that can be used to compute V and R:

RM: Replacing V^2 in the numerator for R I end up with the formula that everyone seems to think is wrong:

V = D^1/3 *R^1/3 (1)

where D is |dX/dtd²Y/dt -d²X/dtdY/dt| ,

RM: I think the algebra is unquestionably correct. But what also convinces me that this is a correct analysis is that I have replicated all the results reported in the power law papers using the above as the computational formulae for V and R above and equation (1) explains all the deviations of the observed power coefficients from 1/3.

RM: But I would like to know why you (and nearly everyone else apparently) thinks this mathematical analysis is false.

Best

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers

On Wed, Sep 7, 2016 at 11:18 PM, Richard Marken rsmarken@gmail.com wrote:

[From Rick Marken (2016.09.07.1420)]

Martin Taylor (2016.09.07.15.39)–

MT: I asked you [Martin Taylor 2016.09.06.09.10] if you would mind

providing a short form explanation of what you claim about the power
law. When I asked the question I thought I understood, but following
your two messages to Warren, I find I don’t understand at all. So
could you just give a quick, non-mathematical description of what
actually IS your explanation of the power law?

RM: Yes, I think it’s a good idea. I was trying to compose it but got waylaid. So here we go again:

RM: The first step in the study of how organisms produce movement trajectories should be the determination of whether or not the trajectories that are observed are purposefully produced – whether or not the movement trajectory or some aspect thereof is a controlled variable. This is very important because physics already has a very good explanation of non-purposefully produced movement trajectories, like those of the planets. So my analysis assumes that the movement trajectories under study are purposefully produced results of an organisms outputs.

RM: Assuming movement trajectories are controlled results of action then power law researchers are measuring two aspects of a controlled variable --its instantaneous curvature and velocity throughout the course of the movement. These two measures of the movement trajectory are presumed to represent variables involved in the production (which in PCT we take to mean control) of the movement. But we know from PCT that it is impossible to see the variables involved in keeping a controlled variable under control by simply observing the behavior of the controlled variable itself.

RM: So the observation of a fairly regular relationship between different measures of a controlled variable (in this case the “power law” relationship between curvature and velocity measures) must be due to something other than a relationship between the variable involved in producing the movement. It turns out that there is a mathematical relationship between the different measures of the controlled variable – curvature and velocity-- that perfectly accounts for the “power law” relationship between these variables that is observed in studies of movement trajectories.

RM: That’s not that quick, I’m afraid. But it’s the best I can do for now. I’ll try to hone it down as I continue to work on it. But I will say that there is a positive implication of this analysis: if you want to understand how people produce purposeful movement, stop asking what the power law suggests about how these movements are produced and start asking what variables are being controlled when people produce these movements. We know the movement is being controlled but that’s pretty general. It should be possible to develop experiments to test whether the velocity of the movement, or the curvature or both are being controlled. Or something else about the movement? And how is this control achieved.

RM: In other words, don’t go chasing illusions; study he real thing – study the fact of control.

Best

Rick

–
Richard S. Marken

“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers