Hello, all –
Apparently, the theory du jour in neuroscience is optimal control theory.
At least that is what Steve Scott uses, and what I see frequently in the
few other discussions I have looked at.
Here is part of a Wikipedia article on the subject. See
http://en.wikipedia.org/wiki/Optimal_control
Don’t try to follow the links – I don’t think they will work since I
just copied these segements from the article. But who knows?
(Attachment b144dc.jpg is missing)
···
==========================================================================
General method
Optimal control deals with the problem of finding a
control law for a given system such that a certain optimality criterion
is achieved. A control problem includes a
cost
functional that is a function of state and control variables. An
optimal control is a set of differential equations describing the
paths of the control variables that minimize the cost functional. The
optimal control can be derived using
Pontryagin’s maximum principle (a
necessary
condition also known as Pontryagin’s minimum principle or simply
Pontryagin’s
Principle
[2]), or by solving the
Hamilton-Jacobi-Bellman equation (a
sufficient
condition).
We begin with a simple example. Consider a car traveling on a
straight line through a hilly road. The question is, how should the
driver press the accelerator pedal in order to minimize the total
traveling time? Clearly in this example, the term control law refers
specifically to the way in which the driver presses the accelerator and
shifts the gears. The “system” consists of both the car and the
road, and the optimality criterion is the minimization of the total
traveling time. Control problems usually include ancillary
constraints. For example the amount of available fuel might be
limited, the accelerator pedal cannot be pushed through the floor of the
car, speed limits, etc.
A proper cost functional is a mathematical expression giving the
traveling time as a function of the speed, geometrical considerations,
and initial conditions of the system. It is often the case that the
constraints are interchangeable with the cost functional.
Another optimal control problem is to find the way to drive the car
so as to minimize its fuel consumption, given that it must complete a
given course in a time not exceeding some amount. Yet another control
problem is to minimize the total monetary cost of completing the trip,
given assumed monetary prices for time and fuel.
A more abstract framework goes as follows. Minimize the
continuous-time cost functional
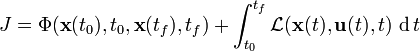
subject to the first-order dynamic
constraints.
=============================================================================
Notice right away what the objective is: it is to minimize a cost
function, given existing constraints, and not to minimize error in some
arbitrary controlled variable. Minimizing cost is a very much more
complex proposition than simply using the available facilities to make
the error as small as possible.
In fact, minimizing cost is minimizing error if the reference condition
to be achieved is zero cost. And cost might be taken to mean the result
of any operation by one control system that increases the error in
another one. Monetary cost is just one variable that might be minimized,
if the system has a limited budget and has to restrict expenditures. And
we could even generalize from there, because the auxiliary variable to be
minimized could actually be the error in another control system – say,
the difference between actual profit and desired profit. In that case,
the cost minimization might actually involve bringing profit to some
specific desired – nonzero – value.
The above excerpt shows how an analyst might derive a design for a
control system, but of course very few organisms know how to do that sort
of mathematics, or any sort, so this does not bring us closer to a model
of an organism even if this approach would work. The writers of the wiki
recognize a similar difficulty, saying
============================================================================
The disadvantage of indirect methods is that the
boundary-value problem is often extremely difficult to solve
(particularly for problems that span large time intervals or problems
with interior point constraints). A well-known software program that
implements indirect methods is
BNDSCO.
[4]
They go on to describe a more practical
approach:
===========================================================================
The approach that has risen to prominence in numerical
optimal control over the past two decades (i.e., from the 1980s to the
present) is that of so called direct methods. In a direct method,
the state and/or control are approximated using an appropriate function
approximation (e.g., polynomial approximation or piecewise constant
parameterization). Simultaneously, the cost functional is approximated as
a cost function. Then, the coefficients of the function
approximations are treated as optimization variables and the problem is
“transcribed” to a nonlinear optimization problem of the
form:
Minimize
![]()
subject to the algebraic constraints
![]()
Depending upon the type of direct method employed, the size of the
nonlinear optimization problem can be quite small (e.g., as in a direct
shooting or quasilinearization method) or may be quite large (e.g., a
direct collocation
method
[5]). In the latter case (i.e., a collocation method), the
nonlinear optimization problem may be literally thousands to tens of
thousands of variables and constraints. Given the size of many NLPs
arising from a direct method, it may appear somewhat counter-intuitive
that solving the nonlinear optimization problem is easier than solving
the boundary-value problem. It is, however, the fact that the NLP is
easier to solve than the boundary-value problem.=======================================================================================
Clearly (to a mathematician, I mean), this ponderous approach will
lead to some sort of design of a control system – or to be more exact,
of a “control law” that will lead to achievement of minimum
cost, however that is defined. But once you set foot on this path there
is no leaving it, because one complexity leads to the need to deal with
another, and complex control processes remain extremely difficult to
handle.
However, the Achilles heel of this approach is to be found, I think, in
the idea of a “control law.” As I understand it, the
“control” of an optimal control system is an output which is so
shaped that when applied to a “plant” or system to be
controlled, the result will be the result that is wanted: what in PCT we
call a controlled variable is brought to a specified reference condition.
Here is a reference to the meaning of “control law:”
http://zone.ni.com/devzone/cda/tut/p/id/8156
========================================================================
A control law is a set of rules that are used to
determine the commands to be sent to a system based on the desired state
of the system. Control laws are used to dictate how a robot moves within
its environment, by sending commands to an actuator(s). The goal is
usually to follow a pre-defined trajectory which is given as the robots
position or velocity profile as a function of time. The control law can
be described as either open-loop control or closed-loop (feedback)
control. =============================================================================
The way this relates to closed-loop control is described this
way:
=============================================================================
A closed-loop (feedback) controller uses the information
gathered from the robots sensors to determine the commands to send to
the actuator(s). It compares the actual state of the robot with the
desired state and adjusts the control commands accordingly, which is
illustrated by the control block diagram below. This is a more robust
method of control for mobile robots since it allows the robot to adapt to
any changes in its environment.
==============================================================================
You can see that they are getting closer, but this is only an illusion.
As shown, this system can’t “adapt to changes in its
environment,” but ff we now think about reorganization, or
“adaptive control”, we find this:
=============================================================================
![[]](http://zone.ni.com/cms/images/devzone/tut/clip_image013_20081206132257.jpg)
Figure 6. An adaptive control system implemented in LabVIEW
===========================================================================
Now we get to the nitty-gritty. Fig. 6 shows what has to go into this
control system model. Note the plant simulation in the middle of it. Note
the “adaptive algorithm” Note the lack of any inputs to
the plant from unpredicted or unpredictable disturbances. And note the
lack of any indication of where reference signals come from. An engineer
building a device in a laboratory doesn’t have to be concerned about such
things, but an organism does. Clearly, for this diagram to represent a
living control system, it will need a lot of help from a protective
laboratory full of helpful equipment, and a library full of data about
physics, chemistry, and laws of nature – the same things the engineer
will use in bringing the control system to life. The engineer is going to
have to do the “system identification” first, which is where
the internal model of the plant comes from – note that the process by
which that model is initially created is not shown.
I’m not saying that this approach won’t work. With a lot of help, it
will, because engineers can solve problems and they won’t quit until they
succeed.
But organisms in general have no library of data or information about
natural laws or protection against disturbances or helpful engineers
standing by or – in most cases – any understanding of how the world
works or any ability to carry out mathematical analyses. This simply
can’t be a diagram of how living control systems work.
The PCT model is specifically about how organisms work. It actually
accomplishes the same ends that the above approach accomplishes, but it
does so in more direct and far simpler ways commensurate with the
capabilities of even an amoeba, and it does not require the control
system to do any elaborate mathematical analysis. It doesn’t have to make
any predictions (except the metaphorical kind of predictions generally
preceded by “You could say that …”). The PCT model constructs
no model of the external world or itself. It does not have to know why
controlled variables occasionally start to deviate from their reference
conditions. It does not need to know how its actions affect the outside
world. When it adapts, it does not do so by figuring out what needs to be
changed and then changing it.
This is not to say that the PCT model has reached perfection or handles
every detail correctly. Nor is it to say that there is nothing in optimal
control theory of any use to a theoretician trying to explain the
behavior of organisms. What I am saying is that PCT provide a far simpler
way of accounting for behavior than the current forms of optimal control
theory seem to provide, and as far as I know can predict behavior at
least as well if not better.
Optimal control theory seems to be a description of how an engineer armed
with certain mathematical tools might go about designing a control system
given the required resources such as fast computers, accurate sensors,
and well-calibrated actuators, in a world where no large unexpected
disturbances occur, or where help is available if they do.
I always think of the robot called Dante, which was sent down into
a dormant volcano with a remote mainframe analyzing its video pictures
for obstacles and calculating where to place (with excruciating slowness)
each of its hexapodal feet, and ended up on its back being hoisted out by
a helicopter.
[
http://www.newscientist.com/article/mg14319390.400-dante-rescued-from-crater-hell-.html
](http://www.newscientist.com/article/mg14319390.400-dante-rescued-from-crater-hell-.html) It stepped on a rock which rolled instead of holding firm. That
kind of robotic design is simply not suited for the real world. As Dante
showed, it is no way to minimize costs. Oh, what we could do with the
money they spent on that demonstration!
Best,
Bill P.
![[]](http://zone.ni.com/cms/images/devzone/tut/image6450.jpg)
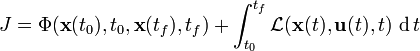
![[]](http://discourse.iapct.org/uploads/default/original/2X/6/6dc055703a342fe6a57f5bee2b2057f81c15d5bb.jpeg)
![[]](http://discourse.iapct.org/uploads/default/original/2X/d/d116103df1e203ed956b5c046eb3cb6789d0aa5a.jpeg)