···
Rupert Young (2014.08.16 15.30)–
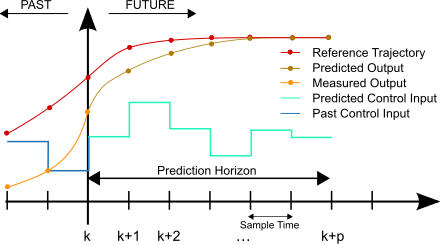
RY: I have been looking around to find a MPC (model-based prediction control) system with a view to showing how it could be reworked in the (simpler) PCT paradigm. I think the following is suitable, “Vehicle adaptive cruise control design with optimal switching between throttle and brake”, http://link.springer.com/article/10.1007/s11768-012-0319-0. I only have a hard copy but can scan and send if required.
RY: It describes an MPC approach to a car cruise control system. But rather than just controlling velocity it also controls the distance to preceding cars and driving “comfort” (which is related to acceleration). They have some very convoluted maths (I can’t say I followed it all) which results in a set of equations which determines the “commands” for throttle and brake. The equations are attached and include, and require, parameters such as vehicle mass, gear ratio, engine torque, wheel radius and gravity (none of which would be available to a human cruise controller, or necessary for a PCT model).
RM: Yes, this might be a good one to implement using a PCT architecture. But they only implemented it in a computer simulation. I suggest that you implement it as an actual physical device (like a Lego vehicle).
RY: Before looking at the PCT version I am curious as to why anyone would take the MPC approach, it seems unnecessarily complex as well as being unrealistic, as above parameters, and physics knowledge, would not be available to a natural controller. Am I missing something?
RM: It’s the Zeitgeist.
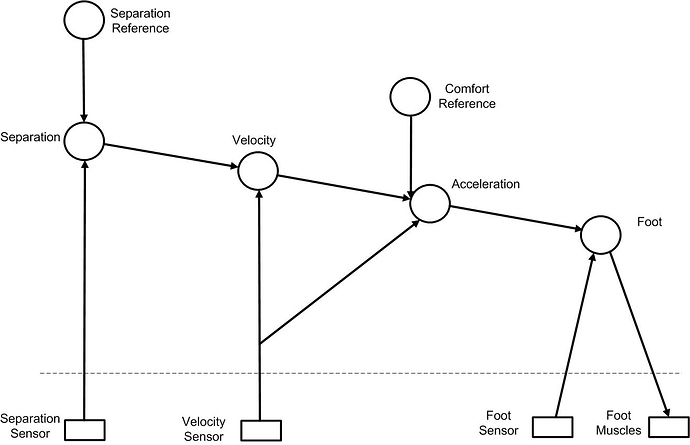
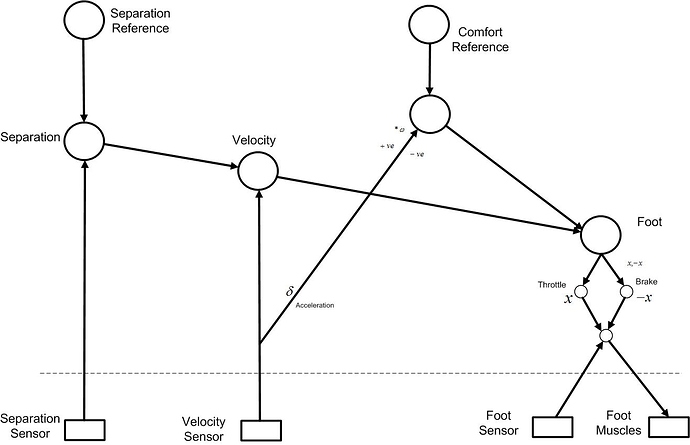
RY: Attached is my draft of the PCT model of this cruise controller. There are two main goals, the separation to the car in front and the “comfort” of driving. The velocity is a function of the separation error, the acceleration is function of the velocity error and the comfort reference and the foot angle is a function of the acceleration error.
RM: I think the main thing the authors of the target paper did was develop an algorithm that would make the switching between accelerator and brake (which is used to control separation) smoother. So all your model would have to do is control for separation smoothly by appropriately varying the activation of accelerator and brake. I believe their algorithm achieves this smoothing by filtering the binary “command signal” (the PCT reference signal) that is sent to either accelerator or brake as appropriate. I can’t tell whether or not this is done in a closed loop. Is their a diagram of their model in the paper? If so, could you post it? If not, never mind; it would take too much time for me to try to figure out their math, if I ever could.
RY: Does this seem valid? Would anyone like to provide a different or improved version? Or provide more detail?
RM: I think your model sketch does need some more detail, and maybe some architectural changes. I understand your diagram (reading left to right) until I get to comfort control. In the diagram comfort seems to be a perception that is a combination of velocity error and velocity. I don’t understand what the combination is – weighted sum? – or why this is a measure of comfort. I think the comfort they are talking about is more like what is called “jerk”, which is a change in (or the derivative of) acceleration. So I would eliminate the “comfort” control system and add a system that perceives and controls “jerk” at 0.
The trick would be to figure out how to switch between brake and accelerator (you can’t vary them simultaneously) appropriately to accelerate (or decelerate) as necessary to maintain separation and doing it so that the perception of jerk is maintained at zero. I think that’s what the Li et al article was about; developing a switching algorithm that provides alternation between brake and accelerator that results in a smooth (no jerk) ride. The trick will be to do this without using the complex computational algorithms described in the Li paper but, rather, to do it the way people do; by controlling perceptions.
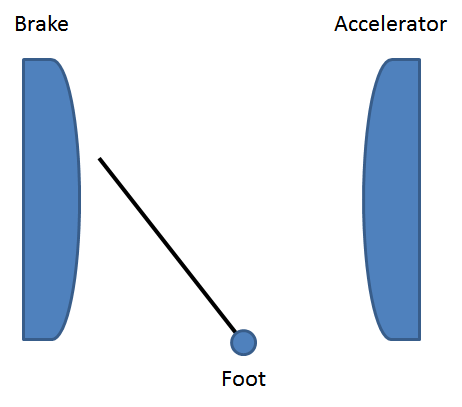
I really have no idea how to actually implement this; I’ll try to work something out in a spreadsheet if I get a chance. But it might just take 99% perspiration and 1% inspiration to get this to work in an actual little Lego car. I envision the output of this car model to be a pivoting arm (analogous to the foot) that can be moved to either hit the accelerator or the brake, as in this little figure:
So the reference for foot position would be a continuous variable that has kind of a binary result, either pressing the brake (with varying pressure) or accelerator (also with varying pressure).
So the problem is to design a perceptual control model that varies foot position between brake and accelerator so that separation distance is maintained “smoothly” (with no “jerk”).
Keep us appraised of your progress on this; the more I think about this the more interesting it becomes.
Best regards
Rick
–
Regards,
Rupert
–
Richard S. Marken, Ph.D.
Author of Doing Research on Purpose.
Now available from Amazon or Barnes & Noble