Hey everybody!
I’m really happy to see this post. I’m really interested in both FEP and PCT and have often thought about how they correspond. I see some things that I want to help clear up a bit as I’m decently familiar with FEP literature/language. I will point out their correspondences in this post and would be happy to get into more detail about it as it will help me learn more of both PCT and FEP!
What does the FEP explain?
It’s helpful to think about this a bit through the lens " Constructor Theory ‘’ here, which is essentially a “principle” based approach to physics. A principle is a statement that constraints the set of possible “subsidiary theories” by immediately eliminating or making impossible “subsidiary theories”. A “subsidiary theory” can also be called a " Mechanical Theory ‘’, it’s the sort of theories we’re familiar with like string theory, quantum mechanics etc… It specifies what the "things’’ you’re dealing with are, as well as the dynamics that those things have. A great example of a principle constraining such theories is the principle of conservation of energy. Any theory which violated the principle of conservation of energy would be HIGHLY suspicious given that all of our currently best theories obey this principle. If such a principle-breaking theory was shown to be correct empirically, then we would know that the principle of conservation of energy is wrong, and would then hunt for deeper principles that both explain our new theory, and allow us to make new ones a bit more easily.
Now that we understand this, we can better understand the Free Energy Principle (FEP). The FEP doesn’t explain anything. Rather, the FEP constrains the set of possible subsidiary, or mechanical, theories GIVEN that the principle is correct. The principle is a reading of a mathematical statement suggesting that “any random dynamical system can be interpreted as performing bayesian inference on its environment”. The mechanical theory that then follows from this is called “Bayesian Mechanics”, which is just to say (roughly), all algorithms/methods that are associated with probabilistic beliefs and updating those beliefs in light of “observations, or evidence”. Since exact Bayesian Inference is often intractable we must approximate it, and one popular method is “Variational Bayesian Inference”, but there are many ways that one can approximate Bayesian inference!
So, the free energy principle doesn’t really refer to “free energy” that we know as a physical quantity, rather, it is talking about the variational (perception information) free energy, and expected (action information) free energy quantities described in variational bayesian inference.
Modeling Perception with Bayesian Mechanics
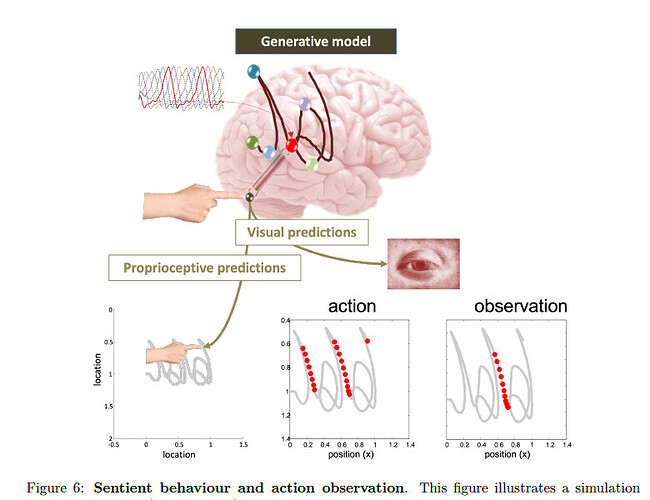
In Bayesian Mechanics any “thing” that exists is treated as trying to infer the hidden causes of its sensory experiences. Sensory experiences are “observations (o)”, and the hidden causes of those experiences are the “states (s)” of the world. Thus, in the simplest case a “thing” embodies a “generative model”, which is a joint probability distribution (o,s), which can be decomposed as: p(o,s) = p(o|s)p(s) OR p(s|o)p(o). The “generative model” is said to be embodied by the “things” physical phenotype, but this is a purely information construct. This generative model is the “prior” in bayesian terms, and constitutes the beliefs the “thing” has about the chances that a particular hidden cause actually caused their particular observation. Using this prior, we can make an inference about the hidden causes of an observation using bayes rule. Here’s bayes rule and how we infer hidden causes of an observation using our generative model under this rule:
- The posterior p(s|o) represents what your beliefs should be after a new observation. This becomes your p(s) in the next round of belief updating.
Recall that direct Bayesian Inference this way is typically intractable; This is because of the computation involving the marginal probability, which can involve integrating over continuous ranges, or simply very large spaces. Due to this, we need to approximate it with variational Bayesian inference. Variational Bayesian Inference is a bit more complicated of a story, and I don’t think we need the details here, but there are some interesting properties that variational inference has.
Variational Bayesian Inference involves the minimization of a function known as the “variational free energy”. Variational Free Energy is the difference between the model complexity and the accuracy of the model; Where complexity is the degree to which a model needs to change when given new sensory input, and accuracy is the ability of the model to predict sensory input. It is explicitly about the informational free energy of the present experience, and implicitly about the free energy of the past.
Modeling Action with Bayesian Mechanics
Of course, we know that “things” take actions, and are not typically passive observers. This is where “Active Inference” comes in. Active Inference can refer to two things: Motor Control in Predictive Coding, and Decision Making in Agents. These are both grounded in Bayesian inference, but the first is about controlling the body to enact a decision, whereas the other is about what decisions to actually make. I think that this second form of Active Inference is most like what PCT does.
To make decisions, an agent needs a way of choosing one action over another. To achieve this, active inference speaks of a “preference” probability distribution p(o|C), which is the probability of a set of observations given one’s preferences. Preferences best capture the notion of “Reference Signal, or Specifications” in PCT. Preferences allow one to calculate what are called “policies (pi)” which is a vector encoding a probability distribution reflecting the value of each policy (i.e. how strongly one believes this policy will lead to a preferred observation). Each policy is a potential series of allowable actions from a vector U, where actions correspond to different state transitions. We can imagine a vector U = [Kick, Punch, Run], and a set of policies { [Kick], [Kick, then run], [Run, then kick, then punch] }. “Pi” is then a distribution over these policies. Since variational free energy can only be calculated with observations, and the value of policies are determined by observations that haven’t happened yet, the value of a policy is calculated using the Expected Free Energy.
Expected Free Energy is the expected cost minus the expected information gain of an action; Where a lower cost value indicates higher reward. Thus, minimizing this function aims to both maximize reward and resolve uncertainty. It is about the free energy expected to be experienced variationally, in the future. Actions, or control mechanisms, in PCT are best captured by the notion of the U vector, and “policies (pi)”, are beliefs about how those actions ought to be employed. So, when an agent acts, you could say that it predicts that this or that policy will lead to this or that observation, which is why it does this or that action.
Using probability distributions to encode preferences and policy values is a sort of mathematical “trick” to bring all elements of action selection within the domain of Bayesian belief updating. We can now consider our generative model to be the joint probability distribution (o,s,pi) which links, perception and action, and couples the agent back to the world by changing it through action. The way we actually model agents/”things” and what-not is typically using a partially observable markov decision process (POMDP).
FEP and PCT as “Unifying Modeling Frameworks”
Modeling with POMDPs and Variational Bayesian Inference is super flexible. Like I think PCT is, Active Inference represents perhaps a “Unifying Modeling Framework”, rather than a prescription about what details to add when modeling a particular thing. For that, you have to do what you normally do… use a combination of intuition and empirical data.
I think that both FEP and PCT seem to allow you to make really good behavioral models once you’ve identified the key features of the “thing” you hope to model on the terms of the modeling framework that you have chosen. Furthermore, I believe both of them can model “things" at any level of scale from “people to particles”, although I haven’t seen an application of PCT to particles as yet. This is an important point, because FEP can describe control systems in terms of beliefs, but it doesn’t necessarily mean to attribute true psychological states like we would say people have. It is only that the same formalism can indeed be used to build a model which simulates the behavior under investigation. So, talk of “uncertainty”, “beliefs”, “surprise”, “information” may not necessarily map to the object of modeling.
I would love to see what the active inference solutions of the “Outfielder Problem” look like compared to PCT solutions.
My “problem” with all “Unifying Model Frameworks” of this sort is that it tells you how you could model any “thing” but doesn’t tell you how to improve your model, or come up with a more mechanistically fine-grained model. We say things like “reference signals” and “beliefs”, but in what forms can these concepts be physically embodied? How can we understand how these things are embodied at multiple levels of scale as they must be in nested hierarchical structures?
Automatically Generating Multiscale Models of Natural Control Systems
It would be great to have models that both capture the behavior under investigation and the mechanisms responsible for that behavior at all relevant scales. Furthermore, I think we’d like to know something about how these natural control systems arose in the first place, as well as how they end up complexifying into larger systems.
I am working on a system capable of producing such models in a principled way and I definitely take strong inspiration from both PCT and FEP. At the last annual IAPCT conference I presented on this system here: https://www.youtube.com/watch?v=dLPpb2Ll3GA&ab_channel=TyfoodsForThought
But didn’t get the chance to go into the more technical details and how exactly it relates to PCT. This system that I have created is an instance of an Eleatic Game, that I call “Hello Game Of Existence (Hello GoE | HGoE)”. Here are the key properties of HGoE:
- The game’s mechanics are turing complete, in that they can be used to set up and run any possible computation.
- The game is both physically and informationally interpretable, in that, the amount of energy required to build a circuit, maintain a circuit, run a circuit and even move a circuit are all quantifiable. This means that the detailed mechanics of the behavior of “things”/models generated by this game can be investigated at every level of scale.
- Circuits can come to encode information about their own existential concerns and take actions on the basis of that information.
- The game allows for indefinite, or “open-ended” complexity growth and this growth can be driven in part through the active minimization of a particular function, which can be said to constitute the “goal” of the eleatic game.
- Information theory of individuality can be used to identify particular “things” generated by the system, and thus to drive diversity metrics, while assembly theory can be used to calculate the complexity of those “things”, to drive complexity metrics.
The existential concerns experienced by the elements of a circuit are quantifiable in terms of “stress”, which is a function of the local environment that the element sits in, and the elements state. This stress value sits between an upper and lower bound which quantify the maximal stress that can be experienced by the element given its state before it ceases to exist. Given that we can find a midpoint between the upper and lower bounds, this midpoint is the “setpoint” or least stressed state of the circuit element. Being least stressed means being further away from nonexistence, and thus, for a “player” of the eleatic game, existence is the controlled variable. Given the capacity of the system, i.e. being that it can actually give rise to very complex natural control systems, one can approach generation in what I see as two promising ways:
- Guided by a human, reinforcement learning agent, or some other kind of “player”. In this case, you have a sort of control system whose goal is to make increasingly complex control systems.
- Guided by local rules that automate the behaviors a player would normally have to do but in a distributed manner. For example, each grid square could be responsible for creating circuit elements, and these circuit elements could then attempt to maintain their own existence by shifting energy around by some dumb, or smart strategy.
Well, that’s my spiel, I’d like to see folks using this principle based approach to create generative systems that produce “physically scrutable” multiscale models of complex intelligent artifacts. I find it to be strongly inspired by the sorts of stuff both the FEP and PCT talk about, except it is aimed at addressing where these things come from in the first place and what they end up evolving into.
I hope that all of this was helpful for the conversation about parallels between FEP and PCT. I really would love to see an Active Inference solution to the outfielder problem and think I will try to make it a pet project so that we can compare it to PCT solutions rigorously. These are no doubt powerful ways to model things, make predictions and understand behavior of natural control systems. I believe that the approach I’ve proposed here is a powerful complement to such approaches and I am excited to see how it might inform them.