(Powers 1971) Feedback analysis of a rat experiment

[amatic]

This is Bill’s paper from 1971 titled A Feedback Model for Behavior: Application to a Rat Experiment. Can be found: here, reprinted in the book Living Control Systems I (1989).

Bill looks to a an experiment of rats pressing levers and avoiding electric shocks, finds from it a model of the rat; then proceeds to predict rat behavior in situations with different probabilities of shock.

Doesn’t look like a very simple read, and shows some unusual analysis, so I thought to discuss it here. For example, it looks like Bill is calculating or estimating the “organism function” of the rat by relating qi (input variable) to R (response).

In the next post, I will look into how Bill estimated the qi, and whether the technique of relating qi and R can be used for estimating the “human function” in a tracking experiment, and how it compares to fitting a model to behavior.

[amatic]

Right off the bat, there are errors in the data. Table 1, column 1 (I, min) shows the intervals in minutes, in which the rat #1 needs to make 8 presses of the lever (rat #2 needs to make 1 press), to not get an electric shock.
The interval listed are: [ 1/4, 1/3, 5/6, 1-2/3, 2-1/2, 5 ].
Judging by the data in the Verhave’s paper (available here) the 4th and 5th intervals should be 1+2/3 and 2+1/2 minutes, or 100 and 150 seconds. So, probably just printing error turned the plus to minus.

The second thing is the function Bill calls “ierf” or “integral error function” and in one place “integral of the error function”. As far as I can find, the error function is already defined as the integral of the normal distribution, doesn’t make much sense to integrate it twice. If someone is sure about the functions Bill used here, chime in. I’ll try to brute force it.

[rsmarken]

Looking forward to it.

[amatic]

I’ve used this Python notebook at Google Colab to explore the data and do all the calculations and plotting. It is possible to just view the code and text or you can copy it and run each code segment (“cell” by clicking the run button). Or you can just read and discuss here.

First plot: empirical data from the experiment by Verhave.

These six values in two variables are all the data we are working with. It comes from a single rat who was trained for several days to press a lever 8 times inside of a time interval. Variable I, as defined by Verhave(1959), is the timer setting of the electric shock circuit. When the rat pressed the lever 8 times (N=8) in less than I minutes, he did not get a shock. Then the timer was reset and the countdown started again. When the timer interval ran out before the rat made 8 presses, he got a shock, and the countdown started again.

The response rate values are average rates of pressing, in presses per second, obtained after training the rats in described way for several days. Each setting of the timer had four 6-hour sessions of training (total 24h per setting). Only the las 4 hours of the last two sessions were included in the average, because by then the rats were showing a relatively stable response rate.

Apparently, researchers were interested in training methods that could obtain high rates of pressing even for long intervals of the timer; for use in avoidance conditioning.

For each value of I (the independent variable), Verhave measured the mean response rate at the end of training (dependent variable). His paper features the following plot of dependent vs independent variable and a curve fitted to the data.

Second plot: fit of the theoretical curve to data
y = 157.38 + 0.1588*x - 79.84 * log(x)

[amatic]

Plot: Redefining the response as an interval instead of rate

Stimulus and response measures are usually pretty arbitrary. Instead of defining the response as a rate of pressing, we can define it as a the average interval that the rat takes to make 8 presses. If we look closer, the stimulus (interval setting) and the response (interval to make 8 presses) are interacting variables. The rat will get a shock only if the the response interval is longer than the shock timer interval setting.

In the diagram bellow, adapted from the paper, variables are represented with lines, and functions are
explicitly written to represent transformations between variables. The diagram represents equations:

  1) Qi = h(S, R)
  2) R  = g(Qi)

               S            Qi         R
             ────> h(S, R) ───> g(Qi) ───┐
                       ^                 │
                       └─────────────────┘

S   - stimulus, applied stimulus, disturbance; interval setting of the shock timer, I
R   - response, organism output, behavior;  response rate, or response interval
Qi  - input quantity, controlled quantity, effective stimulus, sometimes 'behavior';
      note that this is an environmental variable, not a perception; to be found
h() - function relating the qi to applied stimulus and organism response 
g() - organism function, relating the response to the input quantity

We are looking for a variable with a relatively constant value, as this is what characterizes controlled quantities, if we assume a constant reference value. The difference difference between the interval setting (I in seconds) and the response time (Ri, in seconds) is not very constant, and therefore not the controlled quantity, but we have the hint to where it might be.

    Is       Ri      D
-------------------------
  15.0s    6.8s    8.2s
  20.0s    9.0s   11.0s
  50.0s   17.9s   32.1s
 100.0s   33.6s   66.4s
 150.0s   42.9s  107.1s
 300.0s   88.9s  211.1s

[amatic]

Distributions

The experiment was with lever pressing went on for days, and while the response rate was relatively stable, the animals still received electric shock at times, so we are dealing with distributions of response rates in the whole trial. The distributions have indicated averages, but no variance or standard deviation or other measures of distribution width reported. Bill’s solution to this lack of data was to fit a model with a free parameter of distribution width. It would be interesting to test the following methods on a similar experiment with a richer data set reported.

It seems that Bill’s “ierf” function is the same as python’s cdf() or cumulative distribution function. More details on these distributions are in the code.

The two plots can give the same information, one in areas, other in height - the proportion of x bigger than some value X. Or the probability that a random sample from x is bigger than X.
The cdf(x) function is the integral (area under the curve) of the pdf (probability density function) from minus infinity to x. The form 1 - cdf(x) represents the area right of x.

Plot: another way to represent the data from the experiment. Means of distributions are response intervals in seconds (Ri = N/Rp), and the widths of the distributions are hypothetical. Marked areas represent probabilities for shock or proportions of trials that resulted in a shock.

In this plot, the probabilities for shock are not areas, but values on the y axis. Each curve represents one setting of the interval timer. Take the I=15s curve: if the animal presses the lever 8 times in less than 15 seconds it will not get a shock. The higher is the average rate of pressing, the lower is the probability of getting the shock.

[amatic]

Finally, running this code calculates the fit of the hypothetical model with the parameters A (width of the distribution) and k (mouse sensitivity to shocks), to the empirical data.

A = 0.965
k = 546
rates = np.arange(1, 100, .005)
ps_curves = [ ierf (A * (I[i] * rates / N - 1))  for  in range(6)]
rs = []
for i in range(6):
  psk = ps_curves[i] * k 
  intersection = np.argmin(np.abs(rates - psk))
  rs.append(rates[intersection])

I got these values: fairly close to Verhave’s and Bill’s

A=0.965 and k=546
    obs    calc     dif
  70.80   69.71    1.09 
  53.60   55.61   -2.01 
  26.80   26.16    0.64 
  14.30   14.43   -0.13 
  11.20   10.11    1.09 
   5.40    5.45   -0.05 

RMS:  1.066

Running the code with N=1, with the same model also shows a relatively good fit, but there might be something off in the code.

my calc: 12.3, 9.55, 4.21, 2.24
Bill’s 12.32, 9.59 6.59, 4.20
verhave: 13.29, 10.42, 5.93, 3.72

[rsmarken]

This is really nice work, Adam!

Now I think it would be nice to show how the fit to the data is affected by different definitions of the controlled variable. That is, it would be nice to do what Bill did and compare the fit of the model with q.i = p.s (probability of a shock) versus q.i = r.s (rate of shock) as the controlled variable. Bill did this as a demonstration of a model-based version of the Test for the Controlled Variable. I actually think this was one of the most important points of the paper – that you have to know what the organism is controlling in order to correctly understand its behavior. But he kind of buried the lede by discussing it a kind of offhand comment on p. 561. The comment ends with him saying “The fit [of the model using r.s rather than p.s as the controlled variable] is enough worse to cause this hypothesis to be ranked lower than qi = p”. In other words, he tested two hypotheses about the variable the rat was controlling and found one (shock probability, p.s) to be enough better than the other (shock rate, r.s) to merit saying that p.s was the best estimate of the variable the rat was controlling.

I think it would also be nice to show what is illustrated in Figures 3,4 and 5 in Bill’s paper. Figure 5 in particular would be a good one because it shows that the IV (the setting of the interval timer, I) has a much greater effect on the DV (rate of responding, R.p) than does the form of the “rat function” – the “transfer function” that characterizes the rat’s sensitivity to shock. As Bill says in the caption to Figure 5: “Thus the experiment reveals more about the experimental apparatus than about the rat”. In other words, the observed relationship between I and R.p is an example of what came to be called the “behavioral illusion”. It would be great if you could use your model to make some graphs, analogous to Bill’s Figure 5, to make it as clear as possible that this is the case when you are dealing with a living control system.

Again, this is just super work!

Oh, and on a related note, I realized that there is a nice, objective way of defining a side effect of control. Actually, Richard Kennaway did it in one of his slides on “gait planarity” as a side effect of control. Richard said: "Gait planarity can arise from a simple system that is not trying to produce it, cannot sense it, and does not encode it (emphasis mine). In other words, a side effect of control is any observable result of control system behavior that is not intended (controlled).

Best

Rick

[amatic]

Thanks, good ideas!

Here is testing the different hypothesis for the Qi, the rate of shock. This one actually makes more sense to me, that an animal would control a rate of shocks, rather than “probability”. Maybe it is just me, it was quite difficult to work with probabilities in general, I don’t find them very intuitive. Still, fit is fit.

And here is replicating Figure 5.

There are some differences, though. Figure 5 in the paper is an illustration with ‘fictional’ distributions of rates of pressing, but here I put the distributions from the model (assuming they are correct). Here, each Interval setting curve (full color) has a different slope. For the shortest interval setting, the rate of pressing changes rather much by changing the K of the organism function. On the longer interval settings, the effect of (big) change of K is much lower.

Not the clearest example of the behavioral illusion here, I think. The hypothetical distributions (coming out of the model) have different widths, would be interesting to see some real data on this, on how these distributions look. I’m planning a similar thread and code for the behavior illusion, so we can explore that in more detail.

---

On the side effects, sure, if the effect is not controlled, it is a side effect. The main effect is keeping the cv on the reference level. I agree. The problems come when a side effect needs to be explained. For example, movement tremor is not an intended effect of moving the hand from A to B. It is a side effect of something in the system not working as before, and that specific thing needs to be teased out to explain the side effect.

[rsmarken]

Spendid! I’ll take a closer look and see if I can as come up with some other ideas about how present the results. But I think you’ve squeezed about as much out of this one paper (well, two, Verhave’s and Powers’) as is humanly possible.

As far as the fact that p.s is a better representation of the controlled variable than r.s. That caught me up at first, also, especially since it looks like rate (or something close it it) is what is controlled in food reinforcement studies. But it makes sense to me now because with shock you don’t want the shock to occur at a certain rate, you want it not to occur AT ALL. That is, you want to have 0 probability of a shock happening. This is mathematically equivalent to 0 shock rate - and since control is not perfect and shocks do occur it could look like rate of shock is controlled. But the test seems to reveal that it is actually shock probability.

With food, however, rate makes more sense since you not only want food to happen but you want to get a particular amount of it over time. But, still, it would be interesting to do an operant study that made it possible to test to see whether it’s probability or rate that is controlled in food reinforcement studies. One way to do it would be to vary the size of the food pellet delivered as a consequence on making the appropriate number of responses. If the rat is controlling food probability then the size of the pellet won’t matter; if however the rat is controlling something more like rate – like grams/minute – then pellet size will make a difference. Actually, I think there are studies that show that pellet size does make a difference m-- bigger pellets, lower rate of pressing – so it’s most likely a rate that is controlled in food reinforcement studies and a probability that is controlled in shock avoidance studies.

As far as side effects, you make a good point about things like movement tremor; it’s not an intended effect of moving so by my definition it would be a side effect but it certainly is worth studying to see why it happens. But I think the movement tremors are not really a side effect in the same sense as something like gait planarity. That’s because the tremors are part of the process that produces the intended result – movement; they are in the control loop that produces the movement so an explanation of these tremors should be part of the model of the process that produces it.

The side effects, like gait planarity, that Richard and I talked about in the IAPCT talk are not part of a control loop in the same way that the tremors are. TTo the extent that both tremors and gait planarity are unintended consequences of control, both are side effects (per my definition). But I would call the tremors a relevant side effect because they are part of the process (muscle stretch and contraction) that produced the intended result (movement) and I would call gait planarity (and the other side effects we discussed in our talk) irrelevant side effects because they are not obviously part of the process involved in producing the intended result (gait).

I think that once you have a control model of the behavior under study then you can see whether the phenomenon you observe is a relevant or irrelevant side effect of control. It’s irrelevant if it appears when the model is behaving normally; it is relevant if it doesn’t appear when the model is behaving normally.

Best

Rick

[amatic]

It would be interesting to make a continuous model of the rat in this kind of experiments. There should be a random disturbance somewhere in the loop responsible for the variability in the animal’s rate of pressing. Something like the sum effect of fatigue, noise in the rate generator, etc.

–
I think irrelevant effects to a researcher are only the very weak ones. If an effect is relatively strong and regular, then it needs to be explained. There is a reason for it in the workings of the system, and we can’t claim to understand the system if there are unexplained effects and regularities. If a model doesn’t reproduce the regularities, either as main effects or as side effects, it is not complete.

In the rat model, the width of the rate of pressing distribution apparently depends on the rate of pressing. This is a side effect of some property of the rat. No reason to ignore it just because it is not the controlled variable.

[rsmarken]

Hi Adam

It would be interesting to make a continuous model of the rat in this kind of experiments. There should be a random disturbance somewhere in the loop responsible for the variability in the animal’s rate of pressing. Something like the sum effect of fatigue, noise in the rate generator, etc.

Yes, that would be interesting. But I think the effort would be most useful if it illustrated how parameters of the model would affect the ability to determine what the rat is doing (controlling).

I think irrelevant effects to a researcher are only the very weak ones. If an effect is relatively strong and regular, then it needs to be explained. There is a reason for it in the workings of the system, and we can’t claim to understand the system if there are unexplained effects and regularities. If a model doesn’t reproduce the regularities, either as main effects or as side effects, it is not complete.

I agree. The problem, however, is that researchers tend to treat these regularities (which really aren’t all that regular) as indicating something important about how behavior works. So they tend to get kind of defensive when the explanation of these regularities is shown to be that they are a side effect of controlling. My personal inclination is just to start studying behavior as a control phenomenon that is organized around the control of perceptual variables. I think behavioral science has wasted enough time on regularities that were discovered in the context of a view of behavior as caused output.

In the rat model, the width of the rate of pressing distribution apparently depends on the rate of pressing. This is a side effect of some property of the rat. No reason to ignore it just because it is not the controlled variable.

Actually, it might be a controlled variable, or at least related to one. The control system producing presses is the subsystem of which Bill speaks: “The random variations in bar-pressing rate (random with respect to the subsystem involved in this behavior) provide a way to express the effect of output (rate of pressing) on input, as a smooth function.” The fact that the variance of press rate seems to be proportional to the rate of pressing may be a result of the rat controlling for something like the ratio of time between presses to interval length (I). The only way to see if that’s the case is to test it; it might be a nice test to see if shock avoidance behavior involves nested hierarchically related control systems, the upper level one controlling shock probability and the lower level one controlling the ratio of time between presses to interval length.

Best Rick

[amatic]

The problem, however, is that researchers tend to treat these regularities (which really aren’t all that regular) as indicating something important about how behavior works.

You’re being too vague with “something important”. Tremor does indicate something important being wrong somewhere in the movement control system. Lengths of delays in different control loops do indicate something important about the possible locations of the controlled variables in the hierarchy. One possible mistake is to assume that some property of behavior is the intended property.

So they tend to get kind of defensive when the explanation of these regularities is shown to be that they are a side effect of controlling.

You’re guessing that is the reason why they’re defensive. It just might be they are defensive because you accused them of ignorance in mathematics, and of not knowing how to calculate basic properties of trajectories, etc.

But please, that is for a different thread, this one is about rat experiments. Here too we have an interesting regularity in the pressing rate distributions; or the inverse, 8-press response intervals.

These are the distributions of response intervals for different settings of the shock timer (except for the last one, for visibility). The shock timer interval is on the left limit of shaded areas, indicated in the legend of the plot (I). The mean of the distributions are the the mean response intervals (Ri); or the mean times the rat took to press the lever 8 times, values in the legend. Also in the legend are the calculated probabilities of receiving the shock, the size of the shaded areas.

These probabilities are not equal, the rat received much more shocks for the 15s interval setting than in the 150s interval setting. If there was a 1s shock interval setting, the rat would just get shocked all the time because he wouldn’t be able to press the lever 8 times in less than 1 second. The same information could be seen in the Probability of shock vs rate of pressing plot.

My guess for the differences in the distributions is that the rat just couldn’t press fast enough all the time. He got tired, nervous, etc. The distributions are the result of these random properties, and they might be modeled by a random disturbance. Also, not to forget, these are hypothetical distributions made to fit the data, not empirical ones.

[rsmarken]

Hi Adam

> The problem, however, is that researchers tend to treat these regularities (which really aren’t all that regular) as indicating something important about how behavior works.

You’re being too vague with “something important”. Tremor does indicate something important being wrong somewhere in the movement control system. Lengths of delays in different control loops do indicate something important about the possible locations of the controlled variables in the hierarchy. One possible mistake is to assume that some property of behavior is the intended property.

The regularities I was talking about were the examples Richard and I gave in our IAPCT talk: LOT, power law of movement, invariant movement trajectories, gait planarity. Common to all of these is that they are regularities noticed without any understanding that behavior is a control process. They are regularities that are detected without knowing what perceptual variables the system is controlling. So it is not known whether those regularities reflect something important about behavior or not. And, indeed, when the behaviors involved are looked at through control theory glasses (as we did in our talk) these regularities can be seen as irrelevant side effects of control. The regularities you mention in your reply – purpose tremor, time to react in different control loops – do, indeed, indicate something important about behavior because they are observations of aspects of control.

So they tend to get kind of defensive when the explanation of these regularities is shown to be that they are a side effect of controlling.

You’re guessing that is the reason why they’re defensive. It just might be they are defensive because you accused them of ignorance in mathematics, and of not knowing how to calculate basic properties of trajectories, etc.

Well, I hate to go all psychoanalytic on you but it seems to me that this is a clear case of projection;-) I think it was “they” who were accusing me of ignorance of mathematics and of not knowing how to calculate basic properties of trajectories. Far be it from me to accuse anyone of these things since I am not much of a mathematician and know little about calculating basic properties of trajectories. All I know is that I proposed a simple, testable control model of movement trajectory production that accounts for the existence of the “power law” and the reaction was that it was not very encouraging, to say the least.

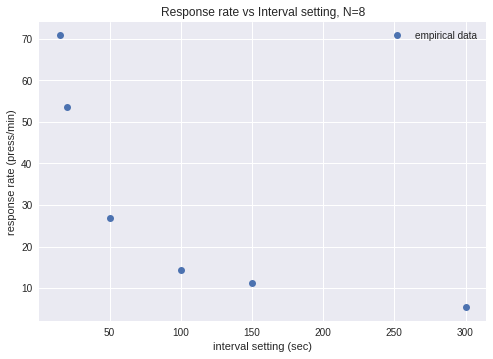
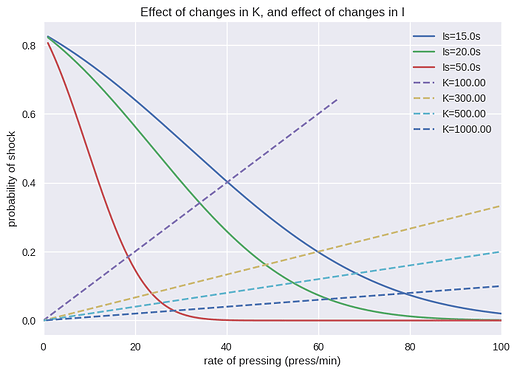
But please, that is for a different thread, this one is about rat experiments. Here too we have an interesting regularity in the pressing rate distributions; or the inverse, 8-press response intervals.

I think Powers’ used the Verhave “rat experiment” to show how to analyze behavior from a control theory perspective. In operant experiments the purposeful nature of behavior is quite obvious; the animal is clearly controlling something about the consequences of its “operants” In this experiment, the rats are clearly controlling something about the shock by pressing the lever.

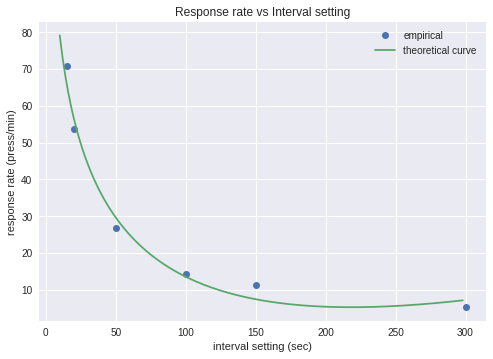
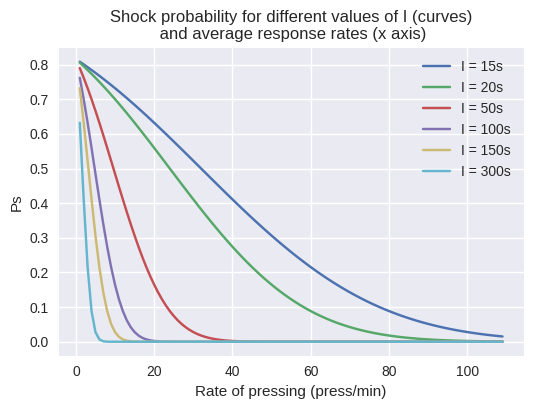
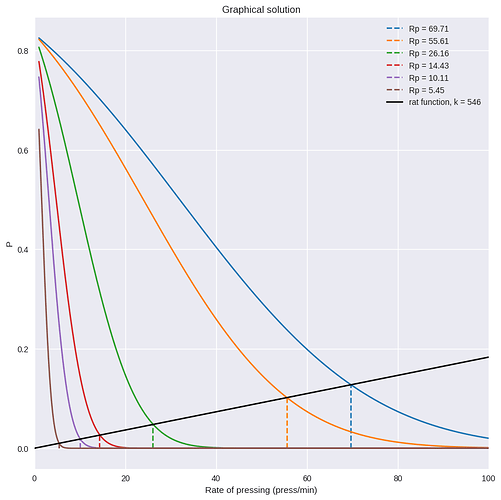
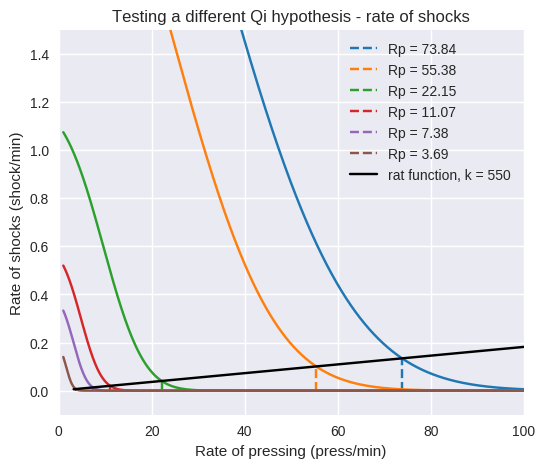
Bill saw that the operant situation was simple enough – and Verhave provided enough information – so that a control model of the behavior could be built. The exercise was useful because it showed that shock avoidance behavior was a control process and that figuring out what perceptual variable the rat was controlling (in this case rate or probability of shock) was central to understanding the observed behavior. The modeling effort also showed that this kind of experiment tells you very little about the rat in terms of its sensitivity to error (the deviation of shock probability from 0). So it is these facts about studying the behavior of control systems that I believe is what the Powers’ (1971) paper is about, and what I think this thread is about.

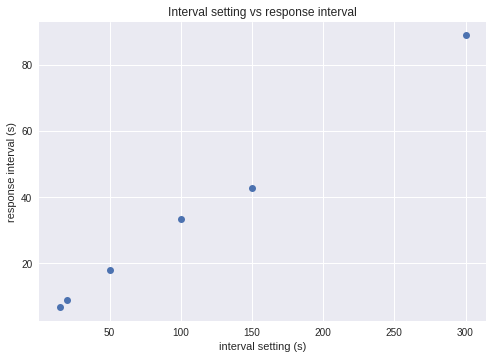
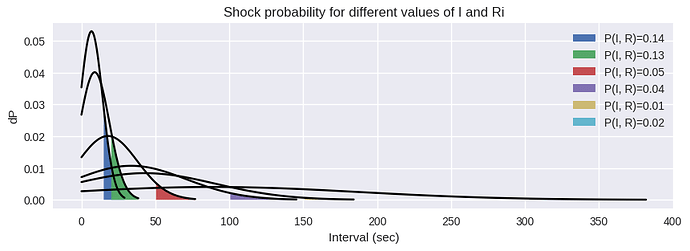
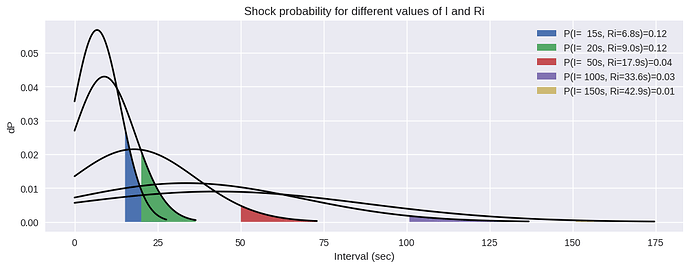
These are the distributions of response intervals for different settings of the shock timer (except for the last one, for visibility)…

These probabilities are not equal, the rat received much more shocks for the 15s interval setting than in the 150s interval setting…

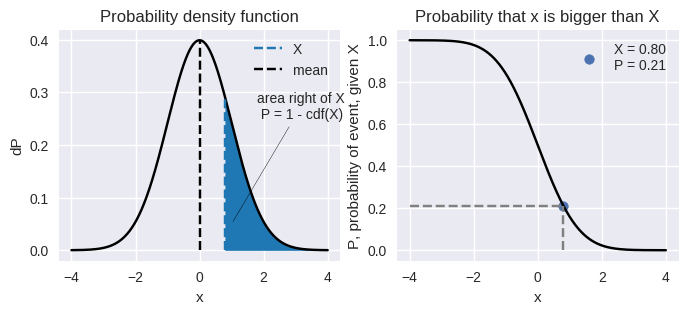
My guess for the differences in the distributions is that the rat just couldn’t press fast enough all the time. He got tired, nervous, etc. The distributions are the result of these random properties, and they might be modeled by a random disturbance. Also, not to forget, these are hypothetical distributions made to fit the data, not empirical ones.

I think what is needed is more data, specifically detailed data on the actual distribution of inter-response intervals (and shock probabilities) in a fixed interval shock avoidance experiment. Then you wouldn’t need to estimate theoretical response interval distributions. Otherwise, I think more modeling given the small amount of data available in the Verhave experiment isn’t going to improve the fit of the model by much.

I think we’ve learned what we can learn from Bill’s (and your) analysis of the “rat experiment”; and what we have learned is something about what to consider when designing experiments aimed at studying the controlling done by living systems. I suggest that the next step might be to design an experiment to determine what variable(s) a person is controlling in a situation might be is of interest to you, such as the variables controlled when a person moves a cursor around a computer screen in various trajectories.

Best

Rick

[amatic]

(the good thing about the discourse platform is that there can be multiple discussions in parallel. I’ll reply in the other thread, and keep this one for possible new stuff about the rat experiments)

I think what is needed is more data, specifically detailed data on the actual distribution of inter-response intervals (and shock probabilities) in a fixed interval shock avoidance experiment. Then you wouldn’t need to estimate theoretical response interval distributions. Otherwise, I think more modeling given the small amount of data available in the Verhave experiment isn’t going to improve the fit of the model by much.

Yeah, it would be great to find a similar experiment with published response distributions. The model would still be interesting in its own right.