Asking for a colleague:
Do you have any great resources on how perceptual control theory relates to programming paradigms, like imperative, functional, or logical programming?
A few years ago I assembled an inventory of the fundamental operations in a digital computer. The purpose was to clear up confusion about the proposed Program level of perception.
All programming languages are merely human-friendly language-like intermediary forms which are transformed to these fundamental operations. The transforming is done by a compiler, by a (compiled) interpreter, or the like.
Broadly, there are arithmetic operations, logic operations, and operations related to storage, input, and output. Those of greatest interest here are the Boolean logic operations, of which the primitive set are AND, OR, and NOT. All the other Boolean operators can be built from (or decomposed to) combinations of these.
Texts on this, on switching theory, and so forth, carry this down to switching of bits in bytes, at the level of machine code. Here’s an example text.
I abandoned this hapless project because there is such a mismatch between bit-switching in a digital computer and the analog interactions of neurons.
Early in the development of computer ‘science’ some sort of demonstration of the computational equivalence of analog and digital computing led to the abandonment of the former, in a “why bother” spirit as the power of the latter was rapidly increasing. Some discussion here.
There is now a growing swing back. Discussion here and here, for example.
A proper comparison would be to the operations and functions in an analog computer. I didn’t proceed to that. I have read the claim that programming languages for analog computers were never developed because there were no general-purpose analog computers, they were all purpose-built. Claude Shannon did develop a mathematical model for a general-purpose analog computer (GPAC) in 1941. Here’s a relevant Wikipedia article.
“Shannon defined the GPAC as an analog circuit consisting of five types of units: adders (which add their inputs), multipliers (which multiply their inputs), integrators, constant units (which always output the value 1), and constant multipliers (which always multiply their input by a fixed constant k). More recently, and for simplicity, the GPAC has instead been defined using the equivalent four types of units: adders, multipliers, integrators and real constant units (which always output the value k, for some fixed real number k).”
Interesting bit of discussion here with a proposal that sounds like reorganization.
Thanks Bruce!
Warren, I found what I started writing up in May of 2020. Here it is, without review or revision.
Where, sorry?
Turns out that .txt is not among the file formats that Discourse supports (jpg, jpeg, png, gif, pdf, doc, docx). Bearing in mind that this was an abandoned draft-in-progress, here’s the content of logic-gates.txt:
Powers assumed that above the Configuration and Transition levels the brain manipulates symbols, just like a digital computer. The following quotations are from Powers (1979).
At the program level, the activities … involve manipulating symbols according to preprogrammed rules and applying contingency tests at appropriate places. (p. 204)
The reason I want category perceptions to be present, whether generated by a special level or not, is that the eighth level seems to operate in terms of symbols and not so interestingly in terms of direct lower-level perceptions. (p. 200)
Perhaps it is best merely to say that this level works the way a computer program works and not worry too much about how perception, comparison, reference signals, and error signals get into the act. I think that there are control systems at this level, but that they are constructed as a computer program is constructed, not as a servomechanism is wired. (p. 201)
Operations of this sort using symbols have long been known to depend on a few basic processes: logical operations and tests. Digital computers imitate the human ability to carry out such processes, just as servomechanisms imitate lower-level human control actions. As in the case of the servomechanism, building workable digital computers has informed us of the operations needed to carry out the processes human beings perform naturally–perhaps not the only way such processes could be carried out, but certainly one way… (p. 202)
I disagree
The heart of programming logic, as he put it, is branching or conditional choice where, after the choice is made, either A is controlled or B is controlled.
At this level, we have what are called contingencies. If one relationship is contingent on another–if a grapefruit will fit into a jar only if its diameter is smaller than that of the jar’s mouth–we can establish the contingent relationship if the other it depends on is also present. (p. 200)
However, the operations of programming logic are not limited to inference. My purpose here is to look more closely at the logical operations and tests that are employed in digital computation, and inquire into “how perception, comparison, reference signals, and error signals get into the act.” If the brain employs the tools of Boolean logic, how might those tools be implemented in neural structures.
There is a more essential issue that I will state here and then defer to a later discussion for which this present essay lays a foundation. If category perceptions function as abstract symbols, the path from a specific controlled variable to a category is straightforward. But once the proposed program-level functions have manipulated those symbols and deduced an abstract conclusion, how do the category perceptions (the symbols) in the conclusion become instantiated as the relevant particular perceptions which are members of those categories? A given program routine may have countless specific applications over time.
A number of logic gates
have been specified to implement functions of Boolian logic
in digital computers. A boolean function returns one of (usually) two values, true/false, and a logic gate returns one of two bit values, 1/0. This Boolean value functions in a program as a control variable– Control flow - Wikipedia a computer science term that must not be confused with the ‘control variable’ which is held constant in an experiment, much less with the controlled variable in a control system. A control variable in digital computation determines the path of program control through the program code.
Control flow - Wikipedia
(Declarative programming ‘languages’
Declarative programming - Wikipedia
handle logic functions without distinct control variables, but this need not concern us here.)
The 16 possible logic gates that take two values as inputs are listed below. Except for the first two, I give three specifications for each:
- The symbolic logic gate definition.
- A perceptual input function, or a synaptic function in a chain of transmission.
- A reference value for controlling input.
For (1), logical True = 1 and logical False = 0. For (2) and (3), I interpret logical True as presence of the specified perception and logical False as its absence.
Null and Identity
Null always returns 0 and Identity always returns 1 regardless of input.
Some systems, for stability, require some pin to be always ‘up’ or always ‘down’. This strikes me as an engineering kludge, but I could be wrong. I see no function for these in control theory. Maybe someone else can.
Transfer
- Pass the value of the input variable.
- A synapse in a chain of transmission for a perceptual signal.
- Input of perception X sets r>0 for control of X.
NOT
- Pass the negated value of the input variable.
- Sense of excitatory signal is changed to inhibitory.
- Input X sets r=0 for control of X.
AND
- Value = 1 only if both input values = 1
- Synapse two excitatory signals to one excitatory signal.
- Input function requires both X and Y in order to generate Z; or Input function requires both X and Y in order to set r>0 for control of Z
NAND
- Value = 0 only if both input values = 1
- Synapse two excitatory signals to one inhibitory signal.
- Input function generates Z unless both X and Y are input (turning Z off); or Input function requires both X and Y in order to set r=0 for control of Z
OR
- Value = 0 only if both input values = 0
- Input function must receive both A and B to generate Z
- Input X or Y sets r>0 for control of Z
NOR
- Value = 1 only if both input values = 0
- Input function generates Z only when both A and B are absent (unlikely input function)
- While controlling Z with r>0, input X or Y sets r=0
Implication
- (If X, then Y) is logically equivalent to (not-X AND Y)
- Input X to input function, it generates Y
- Input X sets r>0 for control of Y
Inhibition (Similar to transfer)
- X and not Y
- Input X, the input function synapses -Y with Y
- Input X sets r=0 for control of Y
EX-OR
- X or Y but not both
- OR combined with inhibition (flip-flop)
- Input X sets r>0 for control of Y and input Y sets r>0 for control of X; or input X and Y sets r=0 for control of Z
EX-NOR
- Value = 1 if X = Y
- NOR (X, Y) combined with inhibition (flip-flop)
- X - Y = 0 sets r>0 for control of Z
Now let’s look a bit more closely at the two senses of disjunction, inclusive (OR and NOR) and exclusive (EX-OR and EX-NOR)
Inclusive or (OR and NOR)
Given any one or more of the set of inputs, the input function generates a perceptual signal. This is Bill’s (1979) proposal for a Category level, a particular form of Relationship input function.
In Bill’s conception, they are simply synapsed together, and the strength of the category relationship perception increases proportionally to the number of distinct perceptions actually input, and their strengths. “Strength of a perception” apparently corresponds to the rate of firing. Strength of a reference signal (rate of firing) specifies the amount of the referenced perception that is to be produced.
But we do not control the category, we control a member of the category. The OR-set is an important function of associative memory that sends reference signals to systems that control aspects of the perception of that category member (those aspects that we might call the criteria for category membership).
Exclusive or (EX-OR and EX-NOR) – either-or
Given two signals, one is admitted to an input function and the other is not. Martin adapted the flip-flop function of digital computer design
He and Rupert developed this notion
as a mechanism for categorial distinctions when the ORed input sets for two categories intersect, and a given input perception (or plurality of perceptions) is in that intersection.
However, it is of more general utility in trial-and-error processes of planning and trouble-shooting. While controlling an outcome in imagination, more than one potential sequence culminating in that outcome may be controlled. The one favored by the flip-flop is pursued unless and until control of it fails, and then another becomes the favored path.
The trial-and-error processes of planning and trouble-shooting often become rather complex, with sequences of sequences, interruptions for sub-sequences, including sequences to arrange environmental feedback functions for control, and alternations between controlling in imagination and controlling through the environment. I began a very limited investigation of these kinds of cognitive processes in the paper that I gave in Manchester in 2019.
This is a continuation of the phenomenological methodology by which Bill Powers identified the levels of the perceptual hierarchy that he proposed.
I think that in context, this is a very useful catalogue. The triune characterizations of the different gates promise to be particularly valuable, whether or not they turn out to be precisely correct.
I was viewing this catalog of logical operators as a basis for a reductio argument: that to claim that the brain controls at a program level by these means leads to absurdity. However, I haven’t pursued it.
I was reflecting yesterday how Rick and I were talking past each other. For him, ‘program control’ is controlling whether a program is running or not. For me, detection of and control of whether or not a program is running happens at a level above the program.
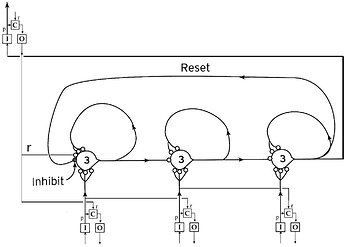
An analogy: Sequence control is accomplished by a chain of ECSs linked together, perhaps in this sort of way:
The linking together of ECSs is at the sequence control level, and the comparator that sends the initial reference signal and receives the perception that the sequence has occurred is at the level above. The interesting stuff is in how it’s done.
Just so, a program level would be below the level that detects whether the program is running or not. The interesting stuff is in what structures constitute and execute the proposed programs.
If there is a logical program level, perhaps it employs something like these 16 Boolean primitives. It is vanishingly unlikely that the brain employs anything like the symbols, syntax, and structures of any of the many programming languages.
Another line of argument: if logic were built into the brain, logicians would be out of work. Boole should have called his book Laws for thought, rather than Laws of thought.
A third line: most (perhaps all) inference reduces to class-inclusion, whence the attractiveness of set theory for e.g. Russell’s logicism (attempting to found mathematics in logic). Every language expresses class relations (Socrates is a man, all men are mortal, ergo Socrates is mortal). I’m sure that would be attacked on well logic-chopped ground. The underlying claim is that logic is a learned discipline, and logic beyond the simplest inferences is a cultural artifact like language, dependent upon common parlance as a precondition.
I think that above sequences we’re looking at what I would call a planning level. There is a ‘logic’ to planning that is not symbolic or linguistic and does not engage the above 16 Boolean programming primitives. It engages input requirements and available or discoverable perceptions in an ad hoc, opportunistic way, by trial and error partly in imagination and partly in practice. The metaphor of programs in a digital computer is a red herring.
Galanter and Pribram’s TOTE is about plans and planning. Their attempt to make it about behavior fails, but cut it back to its proper scope. Bill thought it was a good place to look for examples of programs. I think it’s a good place to look for what in fact they say it’s about: plans and planning.
I think that probably depends on what you mean by “the brain does X by these means”. At one level a single neuron is probably capable of performing all of these gate functions in different parts of itself simultaneously. If so, then the axon firing would result in some kind of integration of the changing result as this and that of its thousands of synapses receive impulses.
But if you mean “the brain does” at the level of operations on Bill’s “neural current”, or at the level of operations on the combinations of perceptual values from lower levels, then I’d probably agree with you, especially since any one perceptual value can be construed as representing the membership in a fuzzy class defined by the perceptual function. The surface logic the brain uses at the neural current level moe or less has to be fuzzy logic, not Boolean logic. Or so it seems to me.
Nevertheless, I still think your catalogue would be useful in considering operations on the discrete/digital side of the category interface. The fuzzy operations are on the analogue side, in the analogue hierarchy, at least in the architecture I have espoused for so many years (back to even before I learned about PCT, as it is described (as a perceptual structure, not a control structure) in the book by my wife and me (“The Psychology of Reading”, Academic Press, 1983) and in chapters by me in other books (e.g. “The Alphabet and the Brain”, de Kerhoce and Lumsden Eds. Springer 1988, or “Artificial and Human Intelligence” Elithorn and Banerji Eds., North Holland 1984). Here’s a quote from the intro to my chapter in the latter:
"At each of several stages, the processes interconnect and can influence each other in both a top-down and a bottom-up way. One of the processes is a careful rule-based analytic process which attempts to produce a unique result; the other is a quicker, approximate pattern matching pattern-matching process that may produce many simultaneous options.
That would be true only if the brain produced a conscious perception of its own operation, and consciously was able to categorize each operator as one of the listed operators, wouldn’t it?
Martin
It is demonstrably unnecessary for us to be conscious of making a logical inference, though of course we often are. Nor does it seem likely to me that the brain has category perceptions of its own operations, conscious or not. Or do I misunderstand?
I’ve only ever actually used that line of argument against those linguists who hold that logic is the basis of semantics in language. It would be difficult to sustain in this less puritanically absolutist context. One can easily say “Well yeah, the brain also does other things, and some of those other things are illogical. Do you think conflict between systems in the brain is unusual?”
People who overtly employ forms of logic generally want to win the argument. In practice, we mostly use trappings of logic to rationalize CVs. Instead of starting from true premises and demonstrating the truth or falsehood of various conclusions relative to them, we assume the truth of a conclusion and marshal evidence from which its truth follows. Contrary evidence, or deduction leading to absurdity, is a disturbance to control of the foregone CV, which we resist.
An alternative that Bill proposed as proper for science is to aim to lose the argument, creatively searching for ways in which your cherished conclusion could be wrong. Karl Popper’s views of “disproof” promote the prevalent gladiatorial conception of science, where you set out to disprove the other guy’s theory, with an implicit presumption favoring your own.