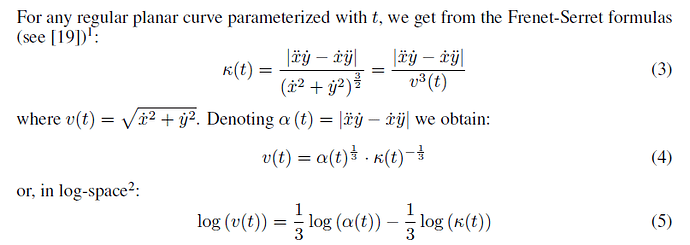Who could have believed that after years of insisting that we should always start from data and not from theory, you now manage to invent a previously (and also afterwards) unknown mathematical law which makes all data obsolete. No mean feat! But, please read on.
RM: Here is the derivation of that “dependence”, per Maoz et al:
It doesn’t matter at all how the “derivation” is done, the end result is that we have the original two variables, in this case velocity (V) and curvature (C), whose internecine correlation we are interested in, and the third variable which is a product of these two in the form (Vx * Cy), in this case it happens to be the so called affine velocity (Va or alpha in original text) in the form (Va = V * C1/3).
RM: The reason velocity, v(t), curvature, kappa(t), and affine velocity, alpha(t), are mathematically related is because they are all functions of the same variables, the first and second derivatives of x and y, which are the coordinates of the changing position of the entity being moved. What this means is that when you are making a planar movement you are simultaneously varying its velocity, curvature and affine velocity.
Yes, they are all functions of the same variables, the x and y components of the movement, but they are that in a certain order and with certain internecine relations: V and C are independent variables so that they do no way determine each other: velocity can be same in steep and gentle curve, and the same curve can be moved with different velocities. Instead affine velocity is a function of both velocity and curve and fully determined by them. It cannot “affect back” to them. This is exactly the same situation as with width, height and area of rectangular.
In the musings about causality in the quotation (as a picture in the original message) from Marken and Shaffer (2017) are bad flaws. The curvature and velocity measured at the same point are simultaneous and so cannot causally affect each other according to the normal view of event causality, that is true. But nothing prevents the curvature in the previous measure point from affecting the velocity in the next point. This can work also in another way around: if you drive too fast to the curve you can slide out from the road. But still much worse failure is to think that the missed third variable which could affect both velocity and curvature could be a variable which itself is a function of them both! Instead as far as I can see the power law researchers have just been searching for those third variables, which of course must be independent physical forces, like just the centripetal force mentioned by Dag.
RM: We already know the physical background of the power law. It’s described in the quote above from Marken & Shaffer (2017): Muscle forces are applied to the entity being moved (a finger or a stylus, for example). Those forces must be enough to compensate for disturbances which include the mass of the entity being moved and any resistive forces (friction, air resistance) affecting it.
Yes, they must be enough to that and in addition they sometimes somehow cause the power relationship between the velocity and curvature, and this is the question: why and how and when?
RM: So in the case of a race driver going around a race course, a negative correlation between speed and the disturbance curvature of the road would reflect a true disturbance-output relationship of a control system – the system controlling the perception of centripetal force. If, however, you looked at the relationship between the curvature and speed of the path of the car itself, you would find something close to the -1/3 power law, which would be an irrelevant side effect of the driver controlling the position of the car.
If there happens to be the curvature-velocity relationship something close to the -1/3 power law and that relationship suits to keep the car on the road then it is not at all an irrelevant side effect but just the means for the driver’s control.
RM: I’ll just end by saying that the importance of understanding the PCT explanation of the power law of movement, as an irrelevant mathematical/ statistical side effect of control, is that it serves as an excellent acid test of one’s understanding of PCT. And so far, no one in this discussion (other than me) has passed the test.
It is always easy to pass self-set tests. I personally really hope that no one else will ever pass it, for the sake of the future of PCT. And I am sorry about your downfall.
RM: Too quote one of our great (and hopefully soon to be incarcerated) ex-presidents: Sad.
Aah, now I understand! You have moved to the post-truth world of alternative facts. Your inventions of that mystical law of the relationship between two variables because of the relationship between three variables and the OVB analysis fit very well to that world. Now, by setting a suitable form and exponents to the third variable and adding it to the predictor variables of a correlation analysis you can produce a strong and exceptionless correlation between any possible two variables with just the slope and power coefficients you happen to wish for. Whoah, if the news about this spread to our world, no one will any more take seriously the unusually high correlations typical to the PCT research.
It would be sad if it were not so funny at the same time.