[From Bruce Abbott (2015.02.12.1250 EST)]
In Part 2 of this series I described the basic circuitry that operates the muscles, and showed how it mediates the tonic stretch reflex that automatically adjusts muscle tension to changes in load. I then described P. A. Merton’s (1954) servo hypothesis of motor control, which proposed that the gamma motor neurons innervating the muscle spindles provide the reference signal of a servo mechanism controlling muscle length. This hypothesis was eventually rejected. In this part I describe the development of an alternative proposal by William T. Powers and his colleagues based on what was later to become known as perceptual control theory, or PCT.
Perceptual Control Theory and Muscle Control
Beginning around 1953, Powers began to develop a way of understanding human and animal behavior based on one central insight: that the function of behavior is control. What is control? For our purposes I will define control as the ability of a system to bring some variable close to a reference value (or “set point”) and keep it there despite the influence of disturbances that would tend to alter its value. Systems that control a variable in this way are called “control systems.” Control systems control by measuring the difference between the reference value and the currently perceived value of the variable to be controlled. This difference, or “error,” drives an output whose effect on the controlled variable is to oppose the influence of disturbances that otherwise would tend to drive the controlled variable away from its reference value. A change in value produced by a disturbance generates an error that in turn produces an output that “feeds back” negatively onto the controlled variable, opposing the effect of the disturbance. Thus control systems are “closed loop” systems that operate using negative feedback to oppose the effects of disturbances. Merton’s servomechanism is one example of a control system.
Control systems usually have a large output gain, meaning that small errors produce large outputs. Because of the closed-loop, negative feedback nature of control systems, as these large outputs begin feed back onto the controlled variable, error between the reference value of the controlled variable and its perceived value quickly diminishes, even before the initially large outputs have had much chance to act. This rapid reduction of error quickly diminishes the feedback, so that in a well-adjusted system there is little or no overshoot, and the system soon brings the controlled variable close to its reference value. Although there are limits to how high the gain can be (dependent on transport lag of signals around the loop and other factors), in general the higher the gain of the system, the more rapidly it can act to correct error and the smaller the residual error will be. I mention this now because the question of gain will become important later when I discuss the effect of “opening the loop” – i.e. eliminating the feedback.
When Powers began to think about applying control theory to human behavior, Norbert Wiener had recently announced and named a new field he called “cybernetics,” the study of “control and communication in the animal and the machine” (Wiener, 1950). This field had grown out of efforts during World War II to develop automated systems for doing such things as accurately aiming anti-aircraft guns at enemy targets and aiming battleship guns accurately despite the rolling of the ship. Early on, workers in this field had recognized that cybernetic principles of control might also underlie biological functioning (e.g.,Rosenbluth, Wiener, & Bigelow, 1943). Now Powers would try to develop a coherent account of human behavior based on the idea that behavior is simply the means by which we bring about intended states of our perceptions.
By 1960, Powers, with colleagues R. K. Clark and R. L. McFarland, had developed Powers’ initial insight into a tentative structural model of the human behavioral system. This model proposed a hierarchy of control systems, beginning at the bottom level with systems controlling perceptions of muscle lengths and tensions. (“Perceptions” are simply scalar signals arising at the bottom level from sensory receptors or combinations of them, and it is the job of the control system to produce actions that bring these perceptions close to their reference values.)
In the model, the references for these “first-level” systems are set by control systems at the next higher level. Setting these references is the next-level system’s means of controlling its own perceptions. In the case of motor control, for example, joint-angle might be the perception to be controlled at the next-higher level. This joint-angle control system would do so by setting the references of first-order systems controlling the lengths of the flexor and extensor muscles that operate the joint in question.
The 1960 version of the model (Powers, Clark, & McFarland, 1960a, 1960b) embraced a nine-level hierarchy based mainly on the authors’ introspections. No attempt was made to relate these levels of control to the anatomy and physiology that might implement these control systems in the human body.
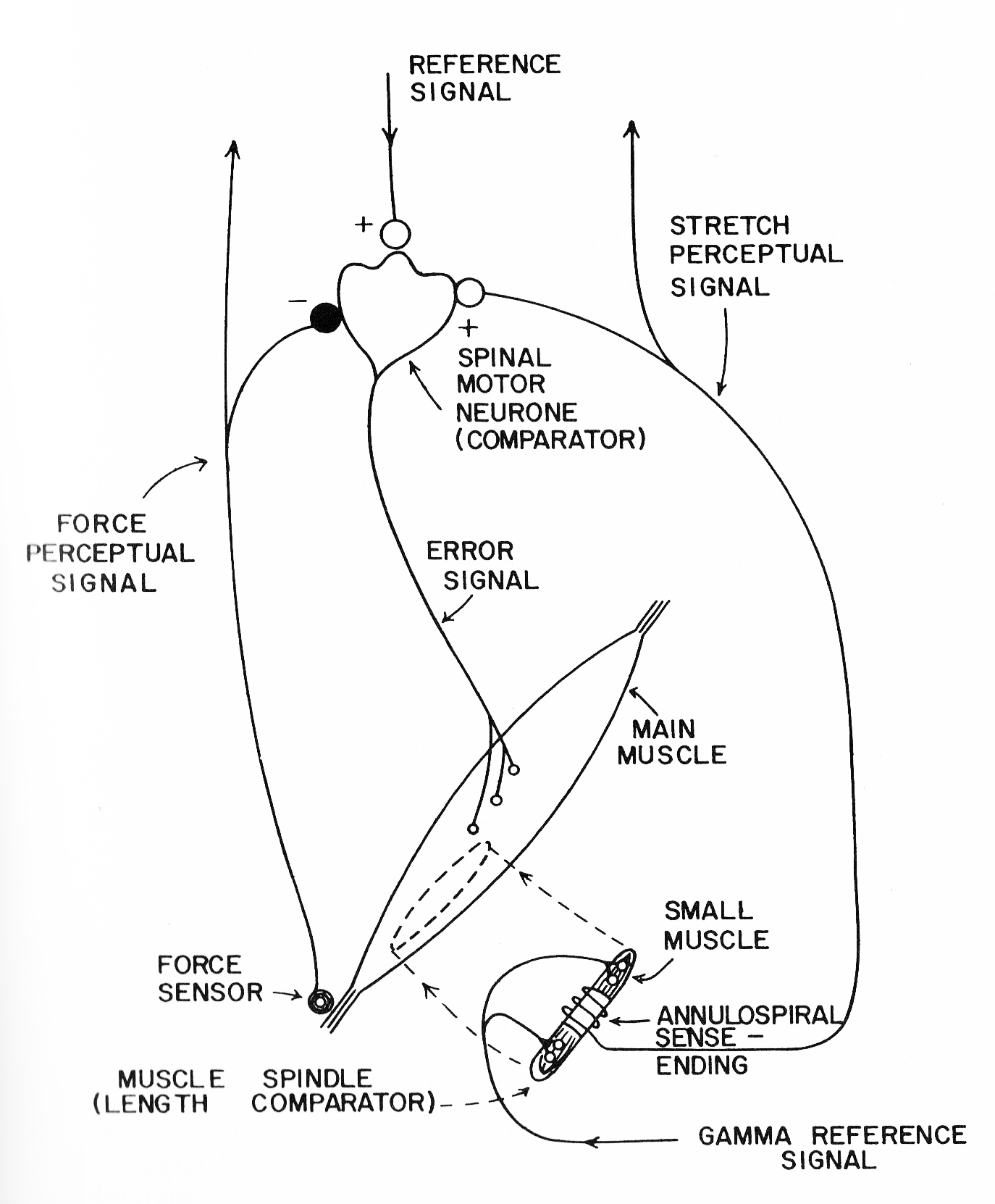
The situation changed with the publication of Powers’ 1973 book, Behavior: the Control of Perception. Chapter 7 lays out a detailed model for motor control at the bottom level of the hierarchy, a model built from the same anatomical components on which Merton’s servo hypothesis was based, with the addition of the Golgi tendon organs and their afferent connections with the alpha motor neurons (see figure below, reproduced from Powers, 1973, Figure 7.1).
 Notice that in this model there are two reference signals, one inputting to the alpha motor neuron and the other to the gamma motor neuron. The gamma reference sets the stretch of the center regions of the muscle spindles. According to Powers, the spindle functions as a mechanical comparator, comparing the stretch of the muscle spindle to that of the muscle in which the spindle is embedded. If there is a difference, signals from the spindle that are transmitted to the alpha motor neuron will act to increase the output of the alpha motor neuron, increasing the muscle’s contraction and thus reducing the difference between the length called for by the gamma reference signal and the perceived length of the muscle. This is the mechanism that Merton proposed in his servo hypothesis.
Notice that in this model there are two reference signals, one inputting to the alpha motor neuron and the other to the gamma motor neuron. The gamma reference sets the stretch of the center regions of the muscle spindles. According to Powers, the spindle functions as a mechanical comparator, comparing the stretch of the muscle spindle to that of the muscle in which the spindle is embedded. If there is a difference, signals from the spindle that are transmitted to the alpha motor neuron will act to increase the output of the alpha motor neuron, increasing the muscle’s contraction and thus reducing the difference between the length called for by the gamma reference signal and the perceived length of the muscle. This is the mechanism that Merton proposed in his servo hypothesis.
Unlike Merton’s hypothesis, the Powers model includes the additional reference signal that enters the alpha motor neuron. This reference signal can increase the rate of firing of the alpha motor neuron and thus directly increase the contraction of the muscle, unlike the gamma reference signal, which must first produce a change in spindle contraction and have that change conveyed via an altered rate of impulses in the type 1a afferents to the alpha motor neuron.
One important factor I haven’t mentioned yet is the fact that contraction of the muscle can only act to relieve the stretch imposed on the muscle spindle fibers. Once those fibers are relaxed, the type 1a spindle afferents go silent. This constitutes a loss of information about further changes in muscle length as the muscle continues to contract. Physiologists have proposed that the system avoids this problem by contracting the muscle spindles at the same rate as the main muscle, thus keeping the spindles from going completely slack. In consequence, any stretch of the main muscle will also stretch the spindle, resulting in an active readout of the change in muscle length. This need to contract muscle and spindle together would explain the phenomenon of alpha-gamma coactivation.
Although not explicitly represented in Power’s model, alpha-gamma coactivation could be achieved if the reference signal entering the alpha motor neuron also arrived at the gamma motor neuron. Furthermore, forces acting on the muscle that prevented it from contracting to the degree set by the reference to the alpha motor neuron would produce a discrepancy between the stretch of the muscle and muscle spindle, which would add to the excitation of the alpha motor neuron, generating extra force in the muscle that would reduce the discrepancy. Meanwhile, any changes in applied force acting on the muscle would also produce a discrepancy, leading to a change in muscle force that compensates for the change in applied force – the automatic operation of the stretch reflex.
The Powers model thus overcomes both objections to Merton’s servo hypothesis. Direct stimulation of the alpha motor neuron by the reference input allows the system to respond much more rapidly to reference changes than is possible in Merton’s gamma-operated servomechanism. The model also explains the function of the observed alpha-gamma coactivation that was a problem for Merton’s hypothesis.
The Powers model also handles another problem that Merton’s servo hypothesis could not. This is the effect of cutting the sensory nerves conveying those type 1a and 1b afferent signals back to the alpha motor neurons. Research by Edward Taub , Emilio Bizzi, and their colleagues demonstrated that cutting these nerves did not prevent monkeys from controlling their limbs. In Merton’s system there are no reference signals entering the alpha motor neurons; thus the only way in which these neurons can initiate impulses to contract a muscle is through the feedback pathway from the muscle spindles. Cutting the type 1a afferents should cause a loss of the ability to contract those muscles. The fact that the monkeys were still able to initiate movement violates this prediction. For the Powers model, however, the loss of sensory feedback from the spindles and Golgi tendon organs simply opens the loop. Reference commands sent to the alpha motor neurons still lead to changes in muscle contraction, although the lack of direct sensory feedback means a loss of proproceptive perception of muscle length, muscle tension, and joint angle.
Because control systems typically have gains of ten or higher, opening the loop via deafferentation would be expected to produce much larger muscle contractions for a given level of alpha motor neuron activity than was the case before the surgery. Monkeys undergoing this procedure would soon learn of this via other sensory inputs (primarily visual) and start to adjust the output gain downward. The initial exaggeration of movement would gradually disappear and the monkeys would learn to substitute visual and other relevant sensory inputs for the lost proprioceptive inputs. The quality of that control would never recover its pre-deafferentation level, but at least some degree of control would be restored. This is exactly the pattern of recovery that is observed.
Although Powers presented a model for motor control in 1973, it was not backed up by computer simulations. Affordable personal computers and programming software with which to construct and run such simulations finally made it possible, in the late 1980s, for Powers to begin their development.
Up next: Little Man and two versions of a Level 1 motor-control model.
Bruce
p.s. I would greatly appreciate any constructive comments. In particular, if anything seems unclear of if you spot what you think are factual or logical errors, I would like to hear about these.