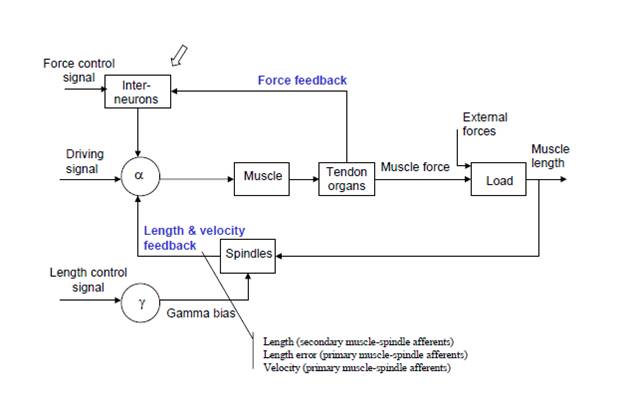
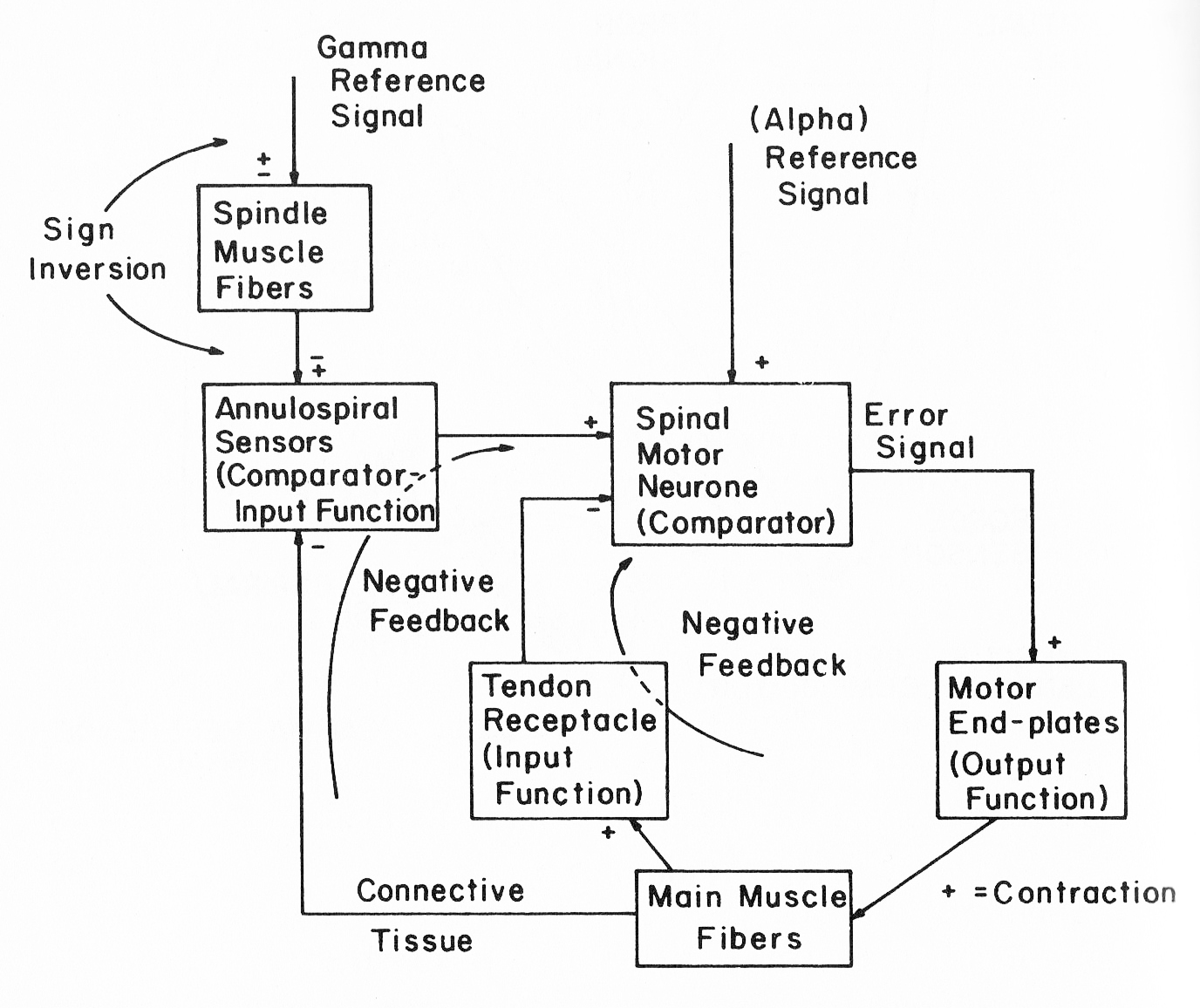
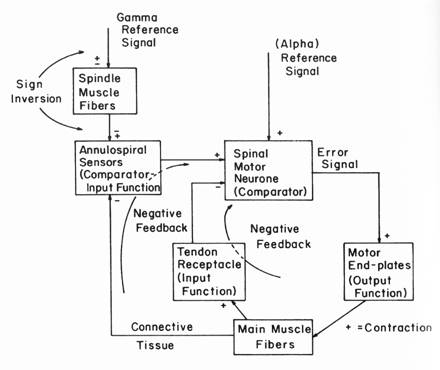
[From Bruce Abbott (2015.03.02.1230 EST)]
If you’ve been following my “Springs and Muscles” series of posts, by now you may be wondering what happened to the next installment, comparing Bill Powers’ PCT-based model of the bottom-level control system to one based on Feldman’s equilibrium-point hypothesis. Well, several issues cropped up that I have had to deal with and it’s been taking me much longer than expected to resolve them. In fact I’m still working on it.
Although I have a nice description of Bill’s model in his 1999 paper describing the “Little Man 2” demo and have the computer code that Bill wrote to implement that model, it wasn’t clear to me how the code represents the model. The paper describes a system with an inner loop that implements control of muscle tension and an outer loop that implements control over muscle length, just as shown in the block diagram presented at Figure 7.4 in B:CP (Powers, 1973). Muscles can only pull, so to control joint angle, nature provides opposing muscles that change joint angle in opposite directions: flexors to close the angle and extensors to open it. However, in his implementation for Little Man 2, Bill chose to replace the flexor-extensor pair with a single “muscle” that can both pull and push. (The “push” represents the pull of the opposing muscle.) According to Bill, this simplified the model by automatically taking account of the reciprocal actions of opposing muscle and the cross-inhibitory neural connections that make this happen, so long as it is assumed that neither muscle becomes completely slack. If that assumption holds, then the two muscles can be represented as a single spring, with a particular length, that can be either stretched or compressed. In the model, the resting position is given a value of zero, so that deviations from this point represent the degree of elongation or compression of the spring.
Bill asserts that real muscles act like strongly nonlinear springs, but by representing opposing muscles with a single spring, the nonlinearities tend to cancel out. Consequently the composite push-pull spring can be represented in the model as a linear spring. In the model, therefore, Hooke’s Law will give a reasonably good approximation to the force generated by muscle contraction or stretch from the neutral position. Thus, multiplying this deviation by the muscle spring constant, ks, gives the force generated by the muscle.
Using this single push-pull muscle may have simplified the implementation of the model, but it also had two unfortunate consequences. First, I found the model as implemented in code much more difficult to understand, and second, the push-pull model does not provide a direct means to produce specified levels of co-contraction, as could be done if the two opposing muscles were represented independently. In the paper Bill states that co-contraction is “absorbed into the effective spring constant,” but the model as implemented provides no means for varying the effective spring constant. The Feldman model to which I intend to compare Bill’s model provides independent reference inputs for reciprocal contraction and co-contraction, and it would be nice to have that same ability in Bill’s model for the purpose of comparison.
Although Bill’ s model works by producing changes in muscle contraction (or stretch) as output, those changes are represented in the model as changes in joint angle, as if joint angle were a linear function of muscle length. This is another simplification, which Bill acknowledges would need to be corrected in a more realistic model. The model also directly computes Torque (force inducing rotation about the joint) rather than the muscle tension or compression that produces the torque.
The environment side represents the limb (whose angle is being changed through joint rotation) in terms of length, mass, and its moment of inertia. These are used to compute the angular acceleration of the limb, which is integrated to give its angular velocity, which is integrated to give its angular position, during each iteration of the simulation loop.
Bill’s original presentation includes two references, one to the alpha motor neuron and the other to the muscle spindles. In Merton’s servo model, varying the spindle reference determined the degree of muscle contraction through feedback to the alpha motor neuron. However, data showed that the alpha and gamma motor neurons tend to be co-activated. In Bill’s model as implemented in Little Man 2, both the alpha and gamma neurons receive the same reference value (and thus are co-activated). There is no provision for manipulating them separately. By separating them I have found that manipulating the alpha reference level produces rather limited changes in joint angle, given the gain factors that Bill found to produce good control. Most of the variation in joint angle can be achieved by varying the spindle reference value by itself. Whether that is realistic or not I do not currently know.
Finally, those gain factors do not seem to match up with what is known about the physiology of the system. Perhaps this is due to the use of linear approximations in the model rather than the various nonlinear relationships known to exist in the real system.
Perhaps this has all led me too far afield – I certainly can compare the PCT and EP models at the diagrammatic level without getting into issues concerning how to implement comparable simulations. But I sure would like to have those two simulations to compare, if only to assure myself that my analyses of the two models and their behaviors are valid.
Bruce
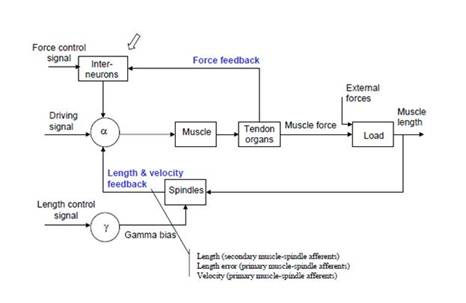
For comparison, at right is the equivalent diagram from Powers (1973). Bill simplified his diagram a bit by omitting the interneurons, which invert the sign of the force signal coming from the Golgi tendon organs; thus the “force control signal” and ‘driving signal” of Shadmehr and Wise’s diagram are combined as the alpha reference signal in Bill’s diagram. Thus the diagram Shadmehr and Wise presented in 2005 is essentially identical to the diagram Bill provided for this same system in 1973.
