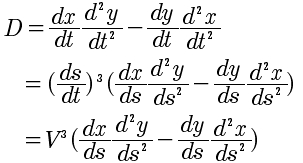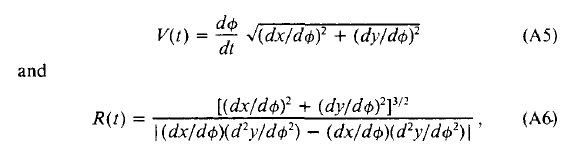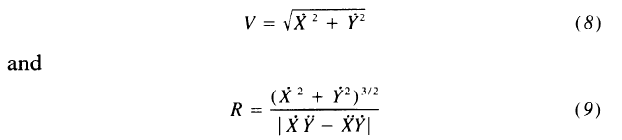[From Bruce Abbott (2017.11.1640 EST)]
In the following I hope to clarify why in the computation of the power law for curved movements, V and R are mathematically independent, so that the observed power-law relationship must emerge from other constraints.
The radius of curvature R of a line at a given point P is the radius of a circle whose curvature best fits the curvature of the line at that point, as shown in the diagram below:
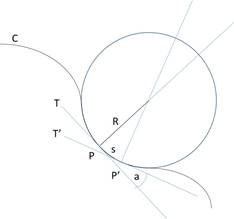
If the line is being drawn by a pen, the velocity V of the pen at point P is the instantaneous velocity tangent to the circle at point P, otherwise known as the tangential velocity.
Gribble and Ostry (1996) used the following formulas to compute V and R from data consisting of a series of X,Y points taken at regular time intervals during the drawing of a figure:
V = (Xdot2 + Ydot2)1/2
R = [(Xdot2 + Ydot2)3/2]/ |XdotYdotdot – XdotdotYdot|
“Xdot” and “Ydot” are the velocities of the point along the X axis and Y axis, respectively. These are the differences between adjacent points along their respective axes, e.g., Xdot = X1 – X0
“Xdotdot” and “Ydotdot” are the corresponding accelerations, taken as the difference between adjacent velocities.
The formula for V recognizes that V is the hypotenuse of a right triangle for which Xdot and Ydot are the opposite sides. According to the Pythagorean Theorem, “The square of the hypotenuse of a right triangle is equal to the sum of the squares of the opposite sides.”
This form appears again in the numerator of the formula for R: [(Xdot2 + Ydot2)3/2], which therefore can be rewritten as V3. The denominator of the formula for R, stated in English, says to take the velocity of the point along the X-axis times its acceleration along the Y axis and from this product, subtract the acceleration of the point along the X-axis times its velocity along the Y-axis, and then take the absolute value of the result. I will refer to this result as the “cross product.”
Now it may seem rather strange that the radius of curvature R should be calculated based on a numerator that is the cube of the point’s tangential velocity. Based on this, you might think that R is some function of tangential velocity. It is not. The reason it is not is found in the cross product.
To explain what the cross product does in the computation of R, I am going to lay out two scenarios. In the first, the line is being traced at a variable velocity along a portion of the curve for which the curvature is constant. In the second, the line is being traced at a constant velocity along a portion of the curve in which the curvature is getting tighter, or in other words, where R is getting smaller.
Case 1: Varying velocity, constant curvature
Let us assume that V is increasing. Consequently, the V-cubed in the numerator of the formula for R is increasing. But so are the velocities and accelerations of the point along the respective X and Y axes increasing. These changes increase the cross product proportionately. The consequence is that although V increases, R remains unchanged. This agrees with our condition that the point is moving around a curve of constant curvature.
Case 2: Constant velocity, variable curvature
Let us assume that the curve is tightening as the point moves long it at a constant velocity. In the formula for R, V-cubed is now constant. However, as the curve tightens, the velocities and accelerations along the X and Y axes are now changing. (How much each changes depends on the current direction of the tangent along which the point is traveling. Given that the curve is tightening, the cross product will be increasing, and as a result, R, the radius of curvature, will grow smaller.
Taken together, these two cases demonstrate the complete mathematical independence of V and R. Given any R whatsoever, V can take any value whatsoever. This agrees with the common-sense notion that the shape of a curve is unrelated to how fast the curve is being traced.
The Power Law for curved movements states that such movements are governed by a power-law relationship between V and R. The law may be expressed as follows: V = kRβ, where k is a constant of proportionality and β is the power exponent. Taking the logarithms on both sides yields this:
Log V = Log k + β Log R
This is a handy form in which to express the law because it makes Log V a linear function of R, which plots as a straight line with Log k as the intercept and β as the slope. Any systematic deviations from linearity are easily spotted on the plot. In many cases, such as freehand scribbles or drawing ellipses, the slope coefficient β has been observed to be close to 1/3.
As noted above, V and R are mathematically independent variables. That V turns out to be a function of R in these cases therefore must be due to some constraints that emerge when tracing such curves. For example, racecar drivers try to go as fast as possible on the straightaways but slow on the curves owing the centrifugal forces acting on the tires during a turn, which threaten to overwhelm the adhesion of the tires to the road surface. This naturally imposes a relationship between the car’s velocity and the racecourse’s curvature.
A contrary opinion has been offered by Marken and Shaffer (2017), who have argued that the power law is a mathematical artifact of the way V and R are computed. Noting that the term in the denominator of the formula for R is V-cubed, they rewrite the formula for R as follows
R = V3/D, where D symbolizes the cross product, |XdotYdotdot – XdotdotYdot|. They then solve the formula in terms of V:
V = D1/3R1/3
Taking the logarithms on both sides yields:
Log V = 1/3 Log D + 1/3 Log R
From this formula they conclude that “power laws may be a statistical artifact inasmuch as the results of the regression analysis used to determine whether the law holds simply reflect a mathematical relationship between the measures of curvature and velocity used in the analysis. In particular, these equations suggest that a regression analysis that includes log(D) as a predictor variable would always find the coefficient of the curvature variable, which corresponds to the estimate of the exponent of the power law, to be exactly equal to its true value, 1/3.”
This analysis is seriously mistaken, as I hope to demonstrate clearly in what follows.
Despite the superficial similarity, the “power law” arrived at based on the formula for R has no bearing on the empirical power law. In the Marken-Shaffer power law, R is a function of V as a consequence of the way in which R is computed. But this formula treats the cross product that appears in the denominator of the formula for R as if it were an independent predictor of V. Yet R itself depends on that same cross product. This logic is equivalent to logic of the following example:
Researchers have been investigating how a certain length variable L varies with area A of a rectangle. As the a point moves along one side of a rectangle, the area of the rectangle increases. Empirically it has been found that, in a particular environment,
L = kA2
Now the area involved is the area of a rectangle, so A = length L times width W. Thus, solving for L,
L = A/W
Following the Marken-Shaffer logic, I conclude that the relationship shown empirically is a mathematical consequence of the fact that area is a function of length.
The flaw in this logic is the assumption that the width W is constant. If the width of the rectangle is changing as its length increases, the area of the rectangle could be related to its length in any number of ways; for example, as the length increases linearly, the width could be increasing as the square root of the length. It is even possible that that the area could remain constant or even decrease as length increases. The Marken-Shaffer analysis would lead to the inclusion of W as the “D” factor in a regression analysis to discover the “hidden variable” due to which the observed relationship departs from the expected one (based on the formula for area) of strict proportionality. This while still asserting that the dependence of length on area is a mathematical consequence of the way in which the area of a rectangle is computed.
The mathematical independence of V and R can be appreciated in another way. Recall that D is the cross product that appears in the denominator of the formula for computing the radius of curvature, R. Its function in the formula is to remove the dependence of R on V so that R becomes a pure measure of shape, independent of the velocity with which the curve is drawn. An easy way to see this is to perform a dimensional analysis to make sure that the units of measure come out right. To make this example concrete, assume that distance is being measured in millimeters (m) and time in seconds (s). Plugging these units into the formula for R yields the following:
V3 = (mm/s)3 = mm3/s3
Xdot = mm/s
Xdotdot = mm/s2
Ydot = mm/s
Ydotdot = mm/s2
R = (mm3/s3)/ |(mm/s)(mm/s2) - (mm/s)(mm/s2)| = (mm3/s3)/(mm2/s3) = mm, a length, as it should be for a radius.
Dividing V3 by the cross product removes time from the measurement of R (the seconds all cancel out), yielding a pure measure of length. Therefore R is independent of V and not of necessity linked to R by a 1/3 (or other exponent) power law (or indeed, any other law). That it is apparently so linked under a variety of circumstances in which curves are being drawn or followed, is the question that researchers in this area have been trying to answer.
Bruce