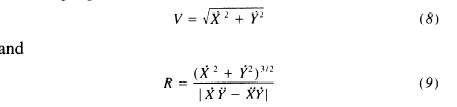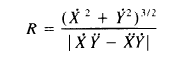Ok will do! Can you send me the software again to record movements as X and Y coordinates over time?
···
On Thu, Jul 28, 2016 at 12:02 AM, Warren Mansell wmansell@gmail.com wrote:
WM: Hi Rick, my block is more about my own mental simulation than being precious about earlier research. You know I am not. Our joint papers reveal that.
It’s just that when I do a fixed curve myself I know that I can change my velocity at will. So that doesn’t obey the law.
RM: But it does. Or, at least, I’m sure it would fit the power law if you would send me the X,Y coordinates of the movement over time. Again, here is a movement pattern I made:
<image.png>
<image.png>
RM: The top graph is the spatial pattern and the lower graph is the temporal pattern of movement in X, Y coordinates. The time trace shows that the speed of movement was changing throughout. The power law coefficient resulting from regressing log (R) on log (V) was .34. The R^2 is only .64. When the log of the D variable is included in the regression the power coefficients for both log(R) and log (D) are exactly .3333 and the R^2 of the regression is 1.0, as predict
ed by my derivation of the relationship between R and V.
WM: Are you saying that ‘to the extent that movement obeys the power law then it is a property of curved motion at a given on-track velocity?’
RM: No. I’m saying that all curved motion seems to obey the power law.
WM: Thus, deviations from the power law would indicate either some purposeful change in velocity for the same curvature (by a PCT system) or a shift in the physics of the environment that the organism cannot immediately counter.
RM: No, I’m saying that the power law has nothing to do with how the curved movement is produced.
WM: I might agree with that. ‘On-track velocity’ is the velocity they your car would register going round a curve, irrespective of its angular velocity. Caravan go different speeds round the same curve.
RM: Right. But if you measured R and V for the pattern of movement traced out by the car you would find the power law relationship between V and R (or A and C). It’s just a mathematical property of curved paths. You slow down and vary your angle of attack through curves because you are controlling your path against force disturbances like gravity, friction, centripetal forces, etc. How we do that is a really inte
resting question and should be studied using the test, as Martin suggested. But the resulting path of the car will obey the power law because the power law is a property of curves paths, regardless of how they were created!! You will find the power law whether the path is a controlled variable (as it is with hand movements and car paths) or not (as in the case of fly larvae and the agents in the crowd demo).
WM: So please put our thoughts about the history of science aside and help me get my head round what you are saying (and what you are not saying).
RM: I hope the above helps. I know it’s kind of astounding to contemplate but, when you think of it, it’s really basic PCT. Movement paths are just something organisms do (intentionally or not) and PCT tells us that you can’t tell what organisms are doing (or how they are doing it) by just looking at what they are doing.
RM: Oh, and I’m still tuning up my spreadsheet demo. I think it could be used to help you understand what’s going on. And I think the best way to do this is for you to record some movement patterns that you think would violate the power law – get at least 1000 equally temporally spaced samples of X,Y points – and lets see whether it does, indeed, violate the power law.
Best regards
Rick
On 27 Jul 2016, at 18:43, Richard Marken rsmarken@gmail.com wrote:
[From Rick Marken (2016.07.27.1040]
–
On Wed, Jul 27, 2016 at 9:56 AM, Warren Mansell wmansell@gmail.com wrote:
W: Hi Rick, what variable is D though, in a PCT loop?
RM: D is not a variable in a PCT loop. D is the term in my derivation of the mathematical relationship between V
and R (or A and C) for any curved movement regardless of how its produced. Here’s the derivation again:
V = D1/3 *R1/3 and A = D1/3 *C2/3
RM: where A = V/R , C = 1/R and D = |X.dotY.2dot-X.2dotY.dot|
RM: So in a log-log regression, for any curve you will find that:
V = .33* log ( |X.dotY.2dot-X.2dotY.dot|) +.33*log (R)
accounts for all the variance in the curve: R^2 = 1.0.
RM: If you just use log (R) as the predictor, you will get coefficients other than .33 as the power coefficient for log (R) and that’s because the variance of |X.dotY.2dot-X.2dotY.dot| is being absorbed into the constant log (K).
WM: I am a bit worried you are experiencing the behavioral illusion.
RM: No, you just don’t understand my analysis. I think it’s because, like Martin and Bruce A., you just can’t believe that 40+ years of power law research that was was aimed at determining how organisms produce curved movement could not possibly have revealed anything about how organisms produce curved movements.
WM: Are you not assuming that the trace of a larva is the purpose of the larva?
RM: Absolutely not! I’m saying that any curved movement will show a power law relationship, whether the curved movement was intentionally produced or a side effect of doing something else (as with the larvae or agents in the crowd program) or produced by a robot, a software simulation or equations. The power law is just a mathematical property of curve
movement; it has nothing to do with how those movements are produced.
WM: Surely the larva cannot plot its movements in X and Y dimensions from an observer’s perspective like in your model? Surely the little larva is controlling for some perception much simpler from it own perspective? Like forward motion on the retina? Then it might control for more intense food smells and veer off in one direction from this path. But it doesn’t have a reference perception of it’s aerial X and Y coordinates does it? Do we necessarily? And other animals?
Please help (yourself?)! Hope I am not being a larva brain too!
RM:No. I just think you have a very strong desire to not offend anyone who shows an interest in PCT. But one
reason I like the discovery about the power law is that it reveals, more clearly than anything I’ve ever seen, why scientific psychologists – even ones who are ostensibly fans of PCT – always get all upset about PCT at some point. It’s because PCT always ends up shows that something that some scientific psychologist considers to be holy writ is not even true.
Best regards
Rick

Warren
On 27 Jul 2016, at 17:30, Richard Marken rsmarken@gmail.com wrote:
[From Rick Marken (2016.07.27
.0930)]
–
Dr Warren Mansell
Reader in Clinical Psychology
School of Psychological Sciences
2nd Floor Zochonis Building
University of Manchester
Oxford Road
Manchester M13 9PL
Email: warren.mansell@manchester.ac.uk
Tel: +44 (0) 161 275 8589
Website: http://www.psych-sci.manchester.ac.uk/st
aff/131406
Advanced notice of a new transdiagnostic therapy manual, authored by Carey, Mansell & Tai - Principles-Based Counselling and Psychotherapy: A Method of Levels Approach
Available Now
Check www.pctweb.org for further information on Perceptual Control Theory
–
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers
–
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers
On Wed, Jul 27, 2016 at 3:55 AM, Warren Mansell wmansell@gmail.com wrote:
WM: …except you don’t always find it because of all those exceptions which we need to understand…
RM: If you mean you don’t always find a perfect 1/3 (.33) power law (for V versus R; let’s stick to that for now) then this observation is explained by my analysis which shows that the relationship between V and R for any movement pattern is:
log V = .33log (D) + .33 log (R). 
;
RM: where D is a variable.
RM: The power law is tested using just log(R) as a predictor of log (V) in the regression analysis. So the regression equation is:
log (V) = log(K) + b * log (R)
RM: where K is a constant. This suggests to me that the regression analysis will only yield a b value that is exactly equal to .33 when the average variance of the .33*log(D) value for a movement pattern allows the regression to find a value for the constant log(K) that results in a b value of exactly .33. Based on the data below, it looks like that is the case:
<image.png>
RM: These a
re r
esults for different ellipses drawn by a simulation model. Notice that the variation in the b value estimates correspond to variation in the log (K) value estimates. Indeed, there is a pretty strong negative correlation (-.63) between the log (K) values and deviations of the b values from .33. This suggests that, indeed, leaving the log(D) term out of the regression is the reason for the variation in estimates of the b value in the power law research
RM: If there is anyone out there who understands my analysis of the power law – especially one who is a skilled mathematician who understands multiple regression analysis in linear algebraic detail (I’m looking at you Richard Kennaway) – it would be nice if you could show exactly how differences in the log (D) term in the equation tha
t describes the relat
ionship between log (V) and log (R) for any figure will affect the value of log(K) and b that is found in a simple linear regression of log (R) on log (V) when log (D) is not included as a predictor variable.
Best regards
Rick
… it doesn’t it mean that V and A have opposing relationships with curvature but as V and A are themselves related, doesn’t this lead to a conflict situation?
Warren
–
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers
On Tue, Jul 26, 2016 at 11:36 PM, Richard
Marken &l
t;rsmarken@gmail.com> wrote:
[From Rick Marken (2016.07.26.1535)]
WM: Mmm, one more thing…
RM: C = 1/R
On Tue, Jul 26, 2016 at 3:23 PM, Warren Mansell wmansell@gmail.com wrote:
RM: I guess if R is
a measure of radius then curvature is inversely related to radius. And maybe curvat
ure does increase with angular velocity and decrease with on-track velocity (whatever that is). And maybe they (whoever they are) do meet in the middle or have some sort of pay off against one another. But, again, what does this have to do with the fact that the power law is a mathematical property of movement in curved paths and has nothing to do with how those movements were created? As I said once before, you will find the 1/3 power law (between V and R or 2/3 between A and C) for any curve, whether it was produced by an equation, a robot, a fly larva or a homicide detective lighting his cigar.( I do feel a lot like one of Colombo’s suspects being toyed with;-)
Best
Rick
–
Dr Warren Mansell
Reader in Clinical Psychology
School of Psychological Sciences
2nd Floor Zochonis Building
University of Manchester
Oxford Road
Manchester M13 9PL
Email: warren.mansell@manchester.ac.uk
Tel: +44 (0) 161 275 8589
Website: http://www.psych-sci.manches
ter.ac.uk/staff/131406
Advanced notice of a new transdiagnostic therapy manual, authored by Carey, Mansell & Tai - Principles-Based Counselling and Psychotherapy: A Method of Levels Approach
Available Now
Check www.pctweb.org for further information on Perceptual Control Theory
On Tue, Jul 26, 2016 at 10:58 PM, Richard Marken rsmarken@gmail.com wrote:
[From Rick Marken (2016.07.26.1455)]
RM: If you were Colombo you would have prefaced your question with “Oh, one more thing…”
RM: Anyway, my evasive answer is: I have no idea what you’re talking about. Where did I say anything about radius being inversely proportional to curvature? Or about on-track and angular velocity? And what does whether or not they meet in the middle have to do with the fact that the power law tells us nothing about how people produce curved movement? Is it somet
hing you want to bring home to Mrs Columbo?
Best
Rick
–
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers
On Tue, Jul 26, 2016 at 2:24 PM, Warren Mansell wmansell@gmail.com wrote:
WM: Hi Rick, I am Colombo
. So radius is inversely proportional to curvature? If so, th
is means that as the curvature increases then angular velocity increases but on-track velocity decreases? Don’t they therefore meet in the middle or have some sort of pay off against one another?
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers