There’s a misunderstanding, right there. A phase plot doesn’t evaluate anything. It describes, and that’s all.
This is the equivalent of saying that you can’t understand how a simple control loop works until you know that the perception being controlled is the depth of water in a particular person’s bathtub.
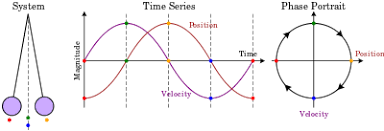
Really? That certainly is not how most users of phase plots interpret them. Let’s try an analogy. A circle is sometimes described as the locus of points equidistant from a given point. That means that a circle plotted as a graph in orthogonal dimensions {x,y} when the “given point” is at {0,0} has the analytic property that every point on the circle of radius d conforms to sqrt(x2+y2) = d, and all points in the space that have this property lie on the circle.
A phase plot is likewise a locus describing the behaviour over time of some variable. Usually, in an x,y plot, “x” represents the value of the variable and “y” represents its derivative. The value of a variable and of its derivative are uncorrelated, though not unrelated. For example, if the derivative,represented by “y” is positive, then “x” is trending in an increasing direction.
None of this depends on what the variable represents or whether it repeats over time. If it does, the phase plot is a closed loop, and quite probably an attractor.
That’s not true either. What the perceptual function (whatever kind of perception it might be) reports at any moment is how similar are the patterns of what its inputs are and have been to whatever it was built to detect.
For example, imagine a sequence detector tuned to the sequence “ABCD…”. When it detects any of these letters, say “B”, its input pattern is more similar to that than it would be if it detected “Z”. If it next detects “C”, the similarity — the value output as that of the current perception — is increased. If it next detects “D” the value is also increased, but by less. It’s increased rather than decreased because there is always the possibility that either the letter detector or the originator missed a step.
Anyway, the point is that all the way through a sequence of events detectable to the senses, every sequence perceiving input function is outputting a value, and if the perception of a particular sequence is being controlled for, the corresponding sequence perception has a reference value and an error value at all times. Either, or any other variable in the sequence control loop could be shown in a phase plot.
I suppose that’s a plausible suggestion. Certainly when you are driving and controlling to keep in your lane, your actual track is defined over time, and a phase plot of, say, your deviation from the lane centre might well suggest whether you had some hidden psychological or physiological problem.