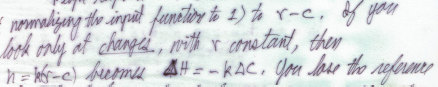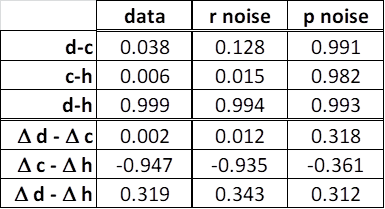Oh Rick, Rick…Ii’ll start charging you my PCT instructions.
Your questions and staements didn’t change at least 6 years. I’ve answered you on the same subject more than 50 x with Bills’ citations ans scientific evidences. Go and look into CSGnet archives. You’ll find all explanaitons you need for answering what you show here that you don’t understand about PCT.
I have enough of repeating the same things all over again.
You have 20 days to scroll out informations you need for understanding what you don’t understand about PCT and “Control of perception”. Then we’ll see if you learned something. For now I’ll just add some of yours citations (from CSGnet archives) and your versions of RCT (older and newer) and Bills’ PCT in form of definitions and diagram LCS III (as usuall. I don’t have time for instruction now, because I’d like to have 20 day peace on sea-side. You should go to.
···
From: Richard Marken (rsmarken@gmail.com via csgnet Mailing List) csgnet@lists.illinois.edu
Sent: Wednesday, July 17, 2019 11:47 PM
To: csgnet csgnet@lists.illinois.edu
Subject: Re: The other “stimulus” (was Re: Please help ID important CSGnet threads)
Manjša : 77.5 x 33.4, debelina 7mm
VeÄ?ja : 80.3 x 34.8, debeline 18mm
[Rick Marken 2019-07-17_14:46:23]
On Wed, Jul 17, 2019 at 12:49 AM “Boris Hartman” csgnet@lists.illinois.edu wrote:
BH: The top problem in RCT thoery is that you still beleive that :
- Behavior is control
- There is some controlled variable in external environment and
- There is some “Controlled Perceptual Variable” or CPV in afferent neuron amd that "perceptual signal behave in control manner … What a construct ???
<
RM: I do believe (1) that behavior is control. I believe it because it is a demonstrable fact. And it is the fact that PCT was developed to explain.
Bill P. at all (50th Anniversary, 2011) : Perceptual Control Theory (PCT) provides a general theory of functioning for organisms.
HB : Demostrate to us how “Behavior is control” with “controlled variable” look like through sleeping… You can also show us how your RCT works throughh many other everyday behaviors.
RM (earlier) : Sleeping is a tough one but I think it is controlling done by the autonomic nervous system that has the aim of keeping some intrinsic physiological variables in genetically determined reference states.
HB : How can people survive with not “controlling behavior” and “controlled variables” in outer environment for more hours. Usually people die if they don’t control for few minutes.
RM :And thanks for getting it right, finally. You typically say that I believe that “behavior is controlled”. I don’t.
RM earlier : I have said that behavior can be controlled. (Search a little bit through archives, you’ll find more)
RM: I don’t believe (2) that controlled variables necessarily exist in the external environment.
HB : What does it mean not “necessarily” ??? Once control and “controlled variable” exist in outer environment and once don’t exist. It’s fifty-fifty ??? Tombola ??? PCT is not Lottery. It’s science which need evidences. And you are not showing them as usual.
RM : Controlled variables above the level of intensity perceptions are assumed to be functions of physical variables. I believe this because it an assumption of the PCT model and I have found that models that control variables that are a function of physical variables account for behavioral data quite accurately.
RM: I have no idea what (3) means.
RM earlier : PCT does assume that the controlled perceptual variable is constructed… (go through archives, you’ll find more)
HB : In your older version of RCT about which you didn’t object for years (go see archives) you were talking about :
-
CONTROL : Keeping of some »aspect of outer environment« in reference state, protected (defended) from disturbances.
-
OUTPUT FUNCTION : controlled effects (control of behavior) to outer environment so to keep some »controlled variable« in reference state
-
FEED-BACK FUNCTION : »Control« of some »aspect of outer environment« in reference state.
-
INPUT FUNCTION : produce »Controlled Perceptual Variable« or »Controlled Perception«, the perceptual correlate of »controlled q.i.«
-
COMPARATOR : ???
-
ERROR SIGNAL : ???
HB : But than recently you changed a little your mind :
RM : And here is my corrected version:
-
CONTROL : Keeping of some aspect of outer environment – the controlled variable – in a reference state, protected from disturbances.
-
OUTPUT FUNCTION : Function that converts an error signal into an output variable that has effects in the environment.
-
FEED-BACK FUNCTION : Physical laws that determine effect of system outputs on a controlled variable.
-
INPUT FUNCTION : Function that converts sensory or perceptual inputs into a perceptual signal that is an analog of the aspect of the environment – the controlled variable – defined by the nature of this function.
-
COMPARATOR : Function that takes a perceptual and a reference signal as input and produces an error signal as output, the error signal being proportional to the difference between the inputs to this function.
-
ERROR SIGNAL : The output of the comparator function.
-
CONTROLLED VARIABLE (or CONTROLLED QUANTITY): The aspect of the environment, defined by the input function, that is controlled by a control system.
HB : We can see that in comparison to Bill’s theory and his definitions of “control loop” these are so big differences that we can easily talk about some strange “non PCT theory”. Why don’t you use your RCT and establish your own forum for theory about “Behavior is control”. Here we are because we beleive in “Control of perception” not behavior.
PCT Definitions of control loop as the core part of Glossary in B:CP :
Bill P (B:CP):
- CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cancel the effects of disturbances.
Bill P (B:CP):
- OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding set of effects on the immediate environment of the system
Bill P (LCS III):…the output function shown in it’s own box represents the means this system has for causing changes in it’s environment.
Bill P (LCS III):
- FEED-BACK FUNCTION : The box represents the set of physical laws, properties, arrangements, linkages, by which the action of this system feeds-back to affect its own input, the controlled variable. That’s what feed-back means : it’s an effect of a system’s output on it’s own input.
Bill P (B:CP) :
- INPUT FUNCTION : The portion of a system that receives signals or stimuli from outside the system, and generates a perceptual signal that is some function of the received signals or stimuli.
Bill P (B:CP) :
- COMPARATOR : The portion of control system that computes the magnitude and direction of mismatch between perceptual and reference signal.
Bill P (B:CP)
- ERROR : The discrepancy between a perceptual signal and a reference signal, which drives a control system’s output function. The discrepancy between a controlled quantity and it’s present reference level, which causes observable behavior.
Bill P (B:CP) :
- ERROR SIGNAL : A signal indicating the magnitude and direction of error.
![cid:image001.jpg@01D37ABE.36063DF0]()
Boris
Rick
It’s obvious that you are changing means to achieve your goal with turning words arround, redefining loop and all nonsesne stuff which has practically nothing to do with science and PCT. It’s wrong goal a far as PCT is concerned. I’m still missing Bills citations and his diagrams, and of course references that would point to him not to your useless “Mindreadings” and tests and so on. The question is whether Powers Ladies will allow you change PCT or at least it’s definition of control ? I’ll try to show what are you trying to change ???
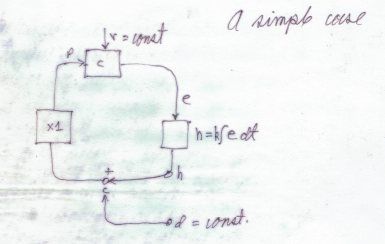
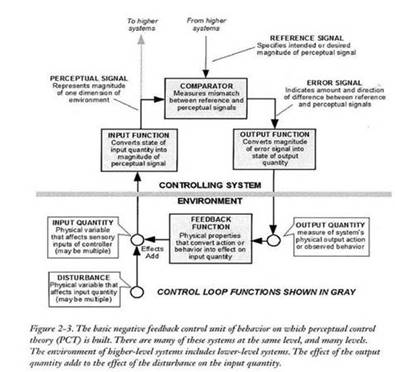
Let us start again with LCS diagram LCS III.
![cid:image001.jpg@01D37ABE.36063DF0]()
RM : Of course, r is determined by an internal reference signal; but that’s just theory.
HB : Do you understand what is reference signal in “fact” or better “reference state” that reference signal is representing ? This is the essence of Bills theory and can’t be just “theory”, because it’s supported with physiological evidences. It’s about how organisms function. Go and look where references are originating. Is genetic engineering theoretical science ? Laser, chemical “scalpels” are just theory and imagination ? Do you have any idea to where science already came ?
By your understanding of physiological functioning of organisms doctors are theoretically recovering people to homeostasis (reference state) ??? How does this theorethical recovering look like in practice ?
It seems that you are dreaming with opened eyes Rick. For you PCT is theorethical playground behind computer (as goes probably for Martin and Bruce Nevin too) and you are drawning the whole CSGnet into “middle age” darkness with your RCT theoretical background. Go and read Bills literature until you’ll understand what in fact Bills PCT is explaining.
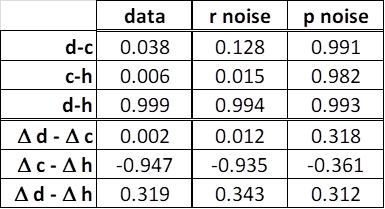
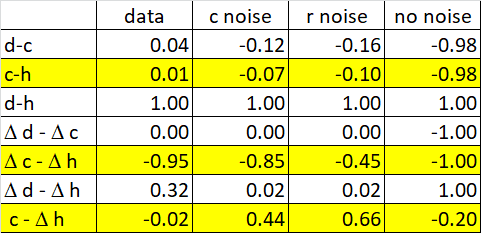
RM : The success of Bill’s little derivation predicting the relationship between ∆h and ∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : I’m really wondering what’s wrong with you. Your picture of how organisms function is pure imagination. It has nothing to do with reality. You are adapting everything in the way to prove your point, which is simply wrong. There is not “Control of output”, there is no “controlled variable” outside and thes is no “controlled input” or CPV.
Explain to us how the relationship between ∆h and ∆c shows that r show existance of reference state of “controlled variable” in environment when you are sleeping, observing, walking, sitting and thinking etc. How many times do I have to tell you that you need to analyse more behaviors and make more experiments so that you can get firm general theoretical background for what you are claiming. Whatever you try to prove has the same problem as Rayleigh–Jeans Law. Experiments and analysis of behaviorss do not confirm your theorethical playground. Where is reference state of a controlled variable in environment when you are sleeping, observing … ?
But let us see how your fantasy can be incorporated into PCT. Maybe will talk also about what’s the value of your fantasy construct in relation to how organisms function.
Bill P (B:CP):
CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cancel the effects of disturbances.
HB : We can see that definition of control in Bills theory does not predict “reference state of controlled variable” outside of the control system but inside control system. There are just reference states inside the system where controlling is done. There is no CANNONICAL PRINCIPLE in PCT.
Your assumption that “reference signal” (r) is just a fiction or theory is wrong. Also assumption that there is some “reference state of controlled variable” outside is wrong because there is no such thing in PCT (see diagram LCS III). If what you are saying is true, Bills definition would look like :
New RCT definition of control :
CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cause reference state in a controlled variable which actually exist in outer environment.
HB : And that is cannonical principle which we already established that is wrong as it means that to the extend that organims control inside they control also outside and vica verse. There is no such thing in PCT although you could explain one or two behaviors that could resemble to what you are saying. On the basis of one or two experiments behind computer you can get explanation or interpretations of behaviors that could be just partial but wrong theory in general sense when trying to explain all behaviors.
So you couldn’t explain mass of behaviors or all of behaviors. Just some. So whatever you are proposing is not general theory. It’s some partial construct.
We have to understand that RCT new definition of control tends to be general as Bill Powers definition of control is general. It is valid for all behaviors. But Ricks is not. So Rick are you proposing a change in Bills general definition of control? Powers ladies (who hates me) probably becasue I’m criticizing Rick, will you support that change ?
HB : If you’ll change definition of control I assume that also other definitions of PCT control loop has to be changed :
Bill P (B:CP):
OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding set of effects on the immediate environment of the system
Bill P (LCS III):…the output function shown in it’s own box represents the means this system has for causing changes in it’s environment.
New RCT definition :
OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding CONTROLLED set of effects on the immediate environment of the system… the means that this system has for causing CONTROLLED CCHANGES to “reference state of controlled variable” that actually exist in outer environment.
HB : Let me remind members again that also this RCT definition has effect of generality. And of course it’s not. It’s valid only for all “controlled behaviors” that are “pushing controlled variable” (Ricks definition of controlled behavior) outside the system into reference state. And that is not what is really happening when organisms behave.
It’s Ricks imagination. Controlled behavior is not “pushing” perception to reference state. It’s easy to prove with any experiment in nature, which is slow enough so that this characteristic of control system can be clearly seen.
Now the “input function”.
In PCT “Input function” is :
Bill P (B:CP) :
INPUT FUNCTION : The portion of a system that receives signals or stimuli from outside the system, and generates a perceptual signal that is some function of the received signals or stimuli.
New RCT definition of “INPUT FUNCTION” :
The portion of a system that receives signals or stimuli from “controlled variable” outside the system which is in reference state or is approaching to reference state, and generates a perceptual signal that is some function of the received signals or stimuli of “controlled variable in reference state” or “controlled variable” outside the system that is approaching to reference state “pushed” by “controlled behavior”.
COMPARATOR : ???
ERROR : ???
ERROR SIGNAL : ???
What a mess… AAs I wrote many times before. There is no place for friendship in science. I hope that all PhD members or members with expert titles will support my statement ? We can not let Rick to promote wrong theory. It’s good friendship gesture, but fatal for PCT as a science.
Boris
P.S. If Powers ladies would need some help in deciding what to do you can write to me. I’ll explain to you in some limits what’s the problem in Ricks RCT thinking. Although I did it for I don’t know how many times. But if you have some “group of experts” who is doing that, why they didn’t “react” ? Do they also think that PCT is about “Control of behavior” and “some controlled variable outside the system” and of course “Controlled Perceptual Variable” or CPV or “Controlled input”.
From: Richard Marken (rsmarken@gmail.com via csgnet Mailing List) csgnet@lists.illinois.edu
Sent: Friday, June 14, 2019 9:15 PM
To: csgnet csgnet@lists.illinois.edu
Subject: Re: The other “stimulus” (was Re: Please help ID important CSGnet threads)
[Rick Marken 2019-06-14_12:13:48]
[Martin Taylor 2019.06.10.23.27]
MT: We are talking ONLY of the nature of an integral.
RM: I think you were the only one talking about an integral. I’m talking about Bill’s little note in his letter to me where he showed that the basic PCT relationship between input and output – h = k(r-c) – implies that ∆h = -k∆c. The equation h = k(r-c) implies that, with r = 0, h = -kc, leading to the expectation that there would be a negative correlation between h and c. But Bill had shown that there is no correlation between h and c in a compensatory tracking task. I confirmed this in my first PCT relevant paper. Bill’s letter pointed out that h = k(r-c) also implies that there will be a correlation between ∆h and ∆c. So I took a look at some tracking data and found that, indeed, there was quite a high correlation between ∆h and ∆c, even though there is a zero correlation between h and c. At first I thought this meant that reference noise was responsible for the low h- c correlation. But my modeling led me to realize that it implied just the opposite; that the low h - c correlation was a result of input noise. And the modeling suggested that this is indeed the case.
RM: You introduced the idea that Bill simple equation for output as a function of input , h = k (r-c), was wrong because it was inconsistent with his diagram. You said it should be h = k∫(r-c)dt which implies that ∆h = -kc, not ∆h = -k∆c, which would imply a high negative correlation between ∆h and c. But there was no such correlation in the data. I believe your claim is that this low correlation is expected due to the nature of integration. If this were the case, the observed correlation between ∆h and c would be constrained be 0 and it wouldn’t be a very interesting piece of data to look at. But in my simulations I’ve found that the correlation between ∆h and c can get to be quite high (> .6) when noise is added to the input (r-c) to the integration. This is based on 3600 samples, which seems like it should be enough to bring the correlation down to zero if, as you say, the correlation between the input to and output from an integral approaches zero if you have enough samples. I think the problem may be that the output function is actually a leaky integration, which behaves more like a filter. But if I continue work on this project you can write one of your brilliant mathematical critiques if I get it published.
RM: But there is still the question of why Bill’s little derivation – ∆h = -k∆c – fits the data and yours – ∆h = -kc doesn’t. This is especially interesting because you believe your equation is based on the correct function relating output to input – h = k∫(r-c)dt – which Bill based his on the wrong one – Bill based his equation on the wrong one – h = k(r-c). But, as usual, I think the mistake is yours, not Bill’s. Your mistake was deriving a relationship between variables ∆h and ∆c from an equation that is part of a set of simultaneous equations that describe the possible functional relationships between variables in a control loop (as shown in Bill’s diagram). To see how the variables in this loop (or their derivatives) are related you have to solve the simultaneous equations that define the loop. Bill derived the relationship between ∆h and ∆c from an equation that describes a relationship between observable variables that is predicted by PCT! The observable variables are c, h and r, where r is the “other stimulus” that Bill mentioned in the letter. It’s a “stimulus” in scare quotes because it is not really a external stimulus variable (like c is) but the state of that variable.Of course, r is determined by an internal reference signal; but that’s just theory. The success of Bill’s little derivation in predicting the relationship between ∆h and ∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : This is something what you want to beleive. First you are claiming that what Martin says that Bill is wrong and you say, that Bill is right. A little later you claim that Bills “r” is just a theory, so he might be wrong. But big Rick Marken solved the riddle. I’m sorry to say Rick. You are bullshitting again.
Give us some other experiments that will work as you predicted in your “mathematical” discourse. You can’t make generalization on one experiment. How many times do I have to repeat that. This is not how organsims function. I can demonstrate you at least 10 experiments which will show that you are wrong about existance of reference states outside no matter how “mathematically” precise you think that you are “calculating” how PCT control loop function.
So it’s sure not true how ever you read Bills notes or diagram what you are saying. There is no reference states of external variables. It’s opposing basic deffinition of control in PCT.
Bill P (B:CP):
CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cancel the effects of disturbances.
If what you are saying is right :
RM : ….predicting the relationshhip between ∆h and ∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : …then it’s obviously that Bills definnition of control is wrong. Will you try to change it ? Will Powers ladies who hates me (because I’m ciriticizing you) allow that ?
Nothing is controlled outside, although behavior involve control as you wrote once. But not for controlling outside but insdie. There are just effects to external environment, not “controlled effects”. If we stick to PCT. But if you want to change also that try.
Bill P (B:CP):
OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding set of effects on the immediate environment of the system
Bill P (LCS III):…the output function shown in it’s own box reepresents the means this system has for causing changes in it’s environment.
HB : You see . There is no “controlled changes”, so that you can “push” external variable into “reference state”.
Only in imagination person which is observing can beleive that “reference state” is outhere. But still that means that references are inside not outside. References outside are illusion (even in tracking experiment you can see that). Bill quite nicely and efficiently described why references outside are illusion. Whatever you are trying to prove has to be in accordance to PCT and all experiments that will be made in future has to be in accordance at least to definitions of control loop in PCT theory. Otherwise you are proving that PCT theory is wrong. I’ll not mention problems which you’ll have when you’ll try to transform your “mathematics” into organisms functioning.
O.K. show us how your “calculations” work in sleeping behavior, observing and for ex. in “forhand shot” which you mentioned in your play.
Where is "reference state of of controlled variable existing outside ??? And there are many more behaviors you’ll have to analyse which will not show any “reference state of controlled variable outside”.
I already explained that you look upon “forehand” behavior from wrong “angle”. It seems that Martin understood what I was saying as he made a copy of similar analysis in “everyday actions”.
I think that problem is that you can’t perceive reference state of some external variable, because reference signal for perceptual variable is inside the system. How can you perceive something that is not yet matched to reference and claime that perception is already showing reference state outside ? Until it is matched to reference signal you can’t say anything about the value of perceptual signal in control sense, because actions (outputs) are not controlled to that level that you can say that actions “pushed controlled variable” outside into reference state and you perceived it. Anyway even if that would be true you could use it only for some behaviors not in general sense. We already established that there is no “canonical principle” in PCT. At least when we are generally speaking about PCT. You can’t make general conclusions on one case. You have to make many case theory. If your PhD is real then you should know how scientifc work should be done.
RM : I think Bill’s point in the letter was that when you look at the correlation between c and h, you get the surprising result of ~0.0 correlation because you are leaving out the “other stimulus” involved in producing h – the reference state of c. When you differentiate h = k(r-c), you get ∆h = -k∆c; that “other stimulus” (r) falls out of the equation and you do see a relationship between ∆h and ∆c.
HB : You think ??? Well you’ll have to try again with another behavior. I think that your thinking is wrong in general sense. You are analyzing Bills’ text from your RCT point of view so you have troubles. You still don’t understand PCT and speccially not how organisms function. Playing with “mathematics” behind computer will not give you solution to understanding all behaviors that human organism can produce. And more behaviors you analyze more precise your theory will be.
Boris
Best
Rick
But if you want to talk correlation, the correlation between the waveform input to an integral and its output waveform approaches zero if you have enough samples. The correlation between h and c must be zero if you have enough independent samples. That’s what you found. …
Ned I say it again in plainer language? I guess so: The long-term correlation between the input and output of an integrator is zero.
At least that’s true for any input waveform that could be represented by a Fourier Transform. It’s not very astonishing that you found this to be true of your simulated integrator.
Proof: Take the Fourier Transform of the input waveform (i.e. represent it as the sum of a set of sine waves calculated appropriately). Consider any one of these sine waves by itself. The output of an integrator that has a sine wave as its input is a cosine wave of the same frequency. A sine wave is uncorrelated with a cosine wave of the same frequency. Since no two of the input sine waves are correlated, no two of the corresponding integrator output cosine waves are correlated. Since all the cosine wave outputs are uncorrelated with the corresponding input sine waves, their sum, which is the output waveform, is uncorrelated with the sum of the input waves, which is the input waveform.
Martin
–
Richard S. Marken
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
–Antoine de Saint-Exupery
–
Richard S. Marken
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
–Antoine de Saint-Exupery
On Wed, Jul 17, 2019 at 12:49 AM “Boris Hartman” csgnet@lists.illinois.edu wrote:
Rick,
it seems that you need “help”… You brought PCT into desperate pposition and I think that we all know this. Whatever you’ve done is irresponsable. Like a child with his toy.
I’ve mentioned many times Rayleigh–Jeans Law. They used wrong interpretation and numbers too describe whatever they thought was happening in physical reality. Physical experiments didn’f feet in their equations. And the same is happening to your “calculations” of control loop. They don’t feet reality or real experiments made in reality.
So you’ll have to prove your new invention with more experiments and everyday behaviors :
RM : The success of Bill’s little derivation predicting the relationship between ∆h and ∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : So Rick we are waiting that you prove your new invention with experiments and analysis of everyday behaviors. Where is “the reference state of controlled variable” outside the system when you are sleeping, sun-bathing, walking, observing… So what we want is to confirm your “new theory”; with “facts”.
If words or numbers turn to describe wrongly what is happening in Reality (and yours words and numbers with no doubt are of this kind) than we have to change interpretations or calculations. I hope you will not say that Reality has to be changed to fit your calculations.
Whatever you wrote or present can’t be confirmed with many behaviors. And that’s what theory is for. To test it in Reality. So why don’t you start conforming your nonsense with behaviors in Reality. Problem is that your theory will not work in 3-D space (because it works only in x and y dimension). When you’ll test your RCT with for ex. 50 behaviors it will turn out that you don’t “control behavior” and that there is no “controlled variable” in environment and that “behavior is not control of perception” because perceptual signal does not behave. Where did you find all that imaginational constructs ???
Most problematic is that your new “invention” is not confirming PCT. You are contradicting as usually. You are trying to change PCT again as so many times before. You have one clear goal. You try to prove that there exist control in outer environment and it can be perceived through “Controlled Perceptual Variable” or CPV.
The top problem in RCT thoery is that you still beleive that :
- Behavior is control
- There is some controlled variable in external environment and
- There is some “Controlled Perceptual Variable” or CPV in afferent neuron amd that "perceptual signal behave in control manner … What a construct ???
It’s obvious that you are changing means to achieve your goal with turning words arround, redefining loop and all nonsesne stuff which has practically nothing to do with science and PCT. It’s wrong goal a far as PCT is concerned. I’m still missing Bills citations and his diagrams, and of course references that would point to him not to your useless “Mindreadings” and tests and so on. The question is whether Powers Ladies will allow you change PCT or at least it’s definition of control ? I’ll try to show what are you trying to change ???
Let us start again with LCS diagram LCS III.
![cid:image001.jpg@01D37ABE.36063DF0]()
RM : Of course, r is determined by an internal reference signal; but that’s just theory.
HB : Do you understand what is reference signal in “fact” or better “reference state” that reference signal is representing ? This is the essence of Bills theory and can’t be just “theory”, because it’s supported with physiological evidences. It’s about how organisms function. Go and look where references are originating. Is genetic engineering theoretical science ? Laser, chemical “scalpels” are just theory and imagination ? Do you have any idea to where science already came ?
By your understanding of physiological functioning of organisms doctors are theoretically recovering people to homeostasis (reference state) ??? How does this theorethical recovering look like in practice ?
It seems that you are dreaming with opened eyes Rick. For you PCT is theorethical playground behind computer (as goes probably for Martin and Bruce Nevin too) and you are drawning the whole CSGnet into “middle age” darkness with your RCT theoretical background. Go and read Bills literature until you’ll understand what in fact Bills PCT is explaining.
RM : The success of Bill’s little derivation predicting the relationship between ∆h and ∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : I’m really wondering what’s wrong with you. Your picture of how organisms function is pure imagination. It has nothing to do with reality. You are adapting everything in the way to prove your point, which is simply wrong. There is not “Control of output”, there is no “controlled variable” outside and thes is no “controlled input” or CPV.
Explain to us how the relationship between ∆h and ∆c shows that r show existance of reference state of “controlled variable” in environment when you are sleeping, observing, walking, sitting and thinking etc. How many times do I have to tell you that you need to analyse more behaviors and make more experiments so that you can get firm general theoretical background for what you are claiming. Whatever you try to prove has the same problem as Rayleigh–Jeeans Law. Experiments and analysis of behaviors do not confirm your theorethical playground. Where is reference state of a controlled variable in environment when you are sleeping, observing … ?
/p>
But let us see how your fantasy can be incorporated into PCT. Maybe will talk also about what’s the value of your fantasy construct in relation to how organisms function.
Bill P (B:CP):
CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cancel the effects of disturbances.
HB : We can see that definition of control in Bills theory does not predict “reference state of controlled variable” outside of the control system but inside control system. There are just reference states inside the system where controlling is done. There is no CANNONICAL PRINCIPLE in PCT.
Your assumption that “reference signal” (r) is just a fiction or theory is wrong. Also assumption that there is some “reference state of controlled variable” outside is wrong because there is no such thing in PCT (see diagram LCS III). If what you are saying is true, Bills definition would look like :
New RCT definition of control :
CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cause reference state in a controlled variable which actually exist in outer environment.
HB : And that is cannonical principle which we already established that is wrong as it means that to the extend that organims control inside they control also outside and vica verse. There is no such thing in PCT although you could explain one or two behaviors that could resemble to what you are saying. On the basis of one or two experiments behind computer you can get explanation or interpretations of behaviors that could be just partial but wrong theory in general sense when trying to explain all behaviors.
So you couldn’t explain mass of behaviors or all of behaviors. Just some. So whatever you are proposing is not general theory. It’s some partial construct.
We have to understand that RCT new definition of control tends to be general as Bill Powers definition of control is general. It is valid for all behaviors. But Ricks is not. So Rick are you proposing a change in Bills general definition of control? Powers ladies (who hates me) probably becasue I’m criticizing Rick, will you support that change ?
HB : If you’ll change definition of control I assume that also other definitions of PCT control loop has to be changed :
Bill P (B:CP):
OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding set of effects on the immediate environment of the system
Bill P (LCS III):…the output function shoown in it’s own box represents the means this system has for causing changes in it’s environment.
New RCT definition :
OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding CONTROLLED set of effects on the immediate environment of the system… the meanns that this system has for causing CONTROLLED CHANGES to “reference state of controlled variable” that actually exist in outer environment.
HB : Let me remind members again that also this RCT definition has effect of generality. And of course it’s not. It’s valid only for all “controlled behaviors” that are “pushing controlled variable” (Ricks definition of controlled behavior) outside the system into reference state. And that is not what is really happening when organisms behave.
It’s Ricks imagination. Controlled behavior is not “pushing” perception to reference state. It’s easy to prove with any experiment in nature, which is slow enough so that this characteristic of control system can be clearly seen.
Now the “input function”.
In PCT “Input function” is :
Bill P (B:CP) :
INPUT FUNCTION : The portion of a system that receives signals or stimuli from outside the system, and generates a perceptual signal that is some function of the received signals or stimuli.
New RCT definition of “INPUT FUNCTION” :
The portion of a system that receives signals or stimuli from “controlled variable” outside the system which is in reference state or is approaching to reference state, and generates a perceptual signal that is some function of the received signals or stimuli of “controlled variable in reference state” or “controlled variable” outside the system that is approaching to reference state “pushed” by “controlled behavior”.
COMPARATOR : ???
ERROR : ???
ERROR SIGNAL : ???
What a mess… As I wrote many times beforre. There is no place for friendship in science. I hope that all PhD members or members with expert titles will support my statement ? We can not let Rick to promote wrong theory. It’s good friendship gesture, but fatal for PCT as a science.
Boris
P.S. If Powers ladies would need some help in deciding what to do you can write to me. I’ll explain to you in some limits what’s the problem in Ricks RCT thinking. Although I did it for I don’t know how many times. But if you have some “group of experts” who is doing that, why they didn’t “react” ? Do they also think that PCT is about “Control of behavior” and “some controlled variable outside the system” and of course “Controlled Perceptual Variable” or CPV or “Controlled input”.
From: Richard Marken (rsmarken@gmail.com via csgnet Mailing List) csgnet@lists.illinois.edu
Sent: Friday, June 14, 2019 9:15 PM
To: csgnet csgnet@lists.illinois.edu
Subject: Re: The other “stimulus” (was Re: Please help ID important CSGnet threads)
[Rick Marken 2019-06-14_12:13:48]
[Martin Taylor 2019.06.10.23.27]
MT: We are talking ONLY of the nature of an integral.
RM: I think you were the only one talking about an integral. I’m talking about Bill’s little note in his letter to me where he showed that the basic PCT relationship between input and output – h = k(r-c) – implies that ∆h = -k∆c. The equation h = k(r-c) implies that, with r = 0, h = -kc, leading to the expectation that there would be a negative correlation between h and c. But Bill had shown that there is no correlation between h and c in a compensatory tracking task. I confirmed this in my first PCT relevant paper. Bill’s letter pointed out that h = k(r-c) also implies that there will be a correlation between ∆h and ∆c. So I took a look at some tracking data and found that, indeed, there was quite a high correlation between ∆h and ∆c, even though there is a zero correlation between h and c. At first I thought this meant that reference noise was responsible for the low h- c correlation. But my modeling led me to realize that it implied just the opposite; that the low h - c correlation was a result of input noise. And the modeling suggested that this is indeed the case.
RM: You introduced the idea that Bill simple equation for output as a function of input , h = k (r-c), was wrong because it was inconsistent with his diagram. You said it should be h = k∫(r-c)dt which implies that ∆h = -kc, not ∆h = -k∆c, which would imply a high negative correlation between ∆h and c. But there was no such correlation in the data. I believe your claim is that this low correlation is expected due to the nature of integration. If this were the case, the observed correlation between ∆h and c would be constrained be 0 and it wouldn’t be a very interesting piece of data to look at. But in my simulations I’ve found that the correlation between ∆h and c can get to be quite high (> .6) when noise is added to the input (r-c) to the integration. This is based on 3600 samples, which seems like it should be enough to bring the correlation down to zero if, as you say, the correlation between the input to and output from an integral approaches zero if you have enough samples. I think the problem may be that the output function is actually a leaky integration, which behaves more like a filter. But if I continue work on this project you can write one of your brilliant mathematical critiques if I get it published.
RM: But there is still the question of why Bill’s little derivation – ∆h = -k∆c – fits the data and yours – ∆h = -kc doesn’t. This is especially interesting because you believe your equation is based on the correct function relating output to input – h = k∫(r-c)dt – which Bill based his on the wrong one – Bill based his equation on the wrong one – h = k(r-c). But, as usual, I think the mistake is yours, not Bill’s. Your mistake was deriving a relationship between variables ∆h and ∆c from an equation that is part of a set of simultaneous equations that describe the possible functional relationships between variables in a control loop (as shown in Bill’s diagram). To see how the variables in this loop (or their derivatives) are related you have to solve the simultaneous equations that define the loop. Bill derived the relationship between ∆h and ∆c from an equation that describes a relationship between observable variables that is predicted by PCT! The observable variables are c, h and r, where r is the “other stimulus” that Bill mentioned in the letter. It’s a “stimulus” in scare quotes because it is not really a external stimulus variable (like c is) but the state of that variable.Of course, r is determined by an internal reference signal; but that’s just theory. The success of Bill’s little derivation in predicting the relationship between ∆h and ∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : This is something what you want to beleive. First you are claiming that what Martin says that Bill is wrong and you say, that Bill is right. A little later you claim that Bills “r” is just a theory, so he might be wrong. But big Rick Marken solved the riddle. I’m sorry to say Rick. You are bullshitting again.
Give us some other experiments that will work as you predicted in your “mathematical” discourse. You can’t make generalization on one experiment. How many times do I have to repeat that. This is not how organsims function. I can demonstrate you at least 10 experiments which will show that you are wrong about existance of reference states outside no matter how “mathematically” precise you think that you are “calculating” how PCT control loop function.
So it’s sure not true how ever you read Bills notes or diagram what you are saying. There is no reference states of external variables. It’s opposing basic deffinition of control in PCT.
Bill P (B:CP):
CONTROL : Achievement and maintenance of a preselected state in the controlling system, through actions on the environment that also cancel the effects of disturbances.
If what you are saying is right :
RM : ….predicting the relationship between ∆h and â∆c shows that r – the reference state of a controlled variable – is a something that actually exists outside of the control system.
HB : …then it’s obviously that Bills definition of control is wrong. Wiill you try to change it ? Will Powers ladies who hates me (because I’m ciriticizing you) allow that ?
Nothing is controlled outside, although behavior involve control as you wrote once. But not for controlling outside but insdie. There are just effects to external environment, not “controlled effects”. If we stick to PCT. But if you want to change also that try.
Bill P (B:CP):
OUTPUT FUNCTION : The portion of a system that converts the magnitude or state of a signal inside the system into a corresponding set of effects on the immediate environment of the system
Bill P (LCS III):…tthe output function shown in it’s own box represents the means this system has for causing changes in it’s environment.
HB : You see . There is no “controlled changes”, so that you can “push” external variable into “reference state”.
Only in imagination person which is observing can beleive that “reference state” is outhere. But still that means that references are inside not outside. References outside are illusion (even in tracking experiment you can see that). Bill quite nicely and efficiently described why references outside are illusion. Whatever you are trying to prove has to be in accordance to PCT and all experiments that will be made in future has to be in accordance at least to definitions of control loop in PCT theory. Otherwise you are proving that PCT theory is wrong. I’ll not mention problems which you’ll have when you’ll try to transform your “mathematics” into organisms functioning.
O.K. show us how your “calculations” work in sleeping behavior, observing and for ex. in “forhand shot” which you mentioned in your play.
Where is "reference state of of controlled variable existing outside ??? And there are many more behaviors you’ll have to analyse which will not show any “reference state of controlled variable outside”.
I already explained that you look upon “forehand” behavior from wrong “angle”. It seems that Martin understood what I was saying as he made a copy of similar analysis in “everyday actions”.
I think that problem is that you can’t perceive reference state of some external variable, because reference signal for perceptual variable is inside the system. How can you perceive something that is not yet matched to reference and claime that perception is already showing reference state outside ? Until it is matched to reference signal you can’t say anything about the value of perceptual signal in control sense, because actions (outputs) are not controlled to that level that you can say that actions “pushed controlled variable” outside into reference state and you perceived it. Anyway even if that would be true you could use it only for some behaviors not in general sense. We already established that there is no “canonical principle” in PCT. At least when we are generally speaking about PCT. You can’t make general conclusions on one case. You have to make many case theory. If your PhD is real then you should know how scientifc work should be done.
RM : I think Bill’s point in the letter was that when you look at the correlation between c and h, you get the surprising result of ~0.0 correlation because you are leaving out the “other stimulus” involved in producing h – the reference state of c. When you differentiate h = k(r-c), you get ∆h = -k∆c; that “other stimulus” (r) falls out of the equation and you do see a relationship between ∆h and ∆c.
HB : You think ??? Well you’ll have to try again with another behavior. I think that your thinking is wrong in general sense. You are analyzing Bills’ text from your RCT point of view so you have troubles. You still don’t understand PCT and speccially not how organisms function. Playing with “mathematics” behind computer will not give you solution to understanding all behaviors that human organism can produce. And more behaviors you analyze more precise your theory will be.
Boris
Best
Rick
But if you want to talk correlation, the correlation between the waveform input to an integral and its output waveform approaches zero if you have enough samples. The correlation between h and c must be zero if you have enough independent samples. That’s what you found. …
Ned I say it again in plainer language? I guess so: The long-term correlation between the input and output of an integrator is zero.
At least that’s true for any input waveform that could be represented by a Fourier Transform. It’s not very astonishing that you found this to be true of your simulated integrator.
Proof: Take the Fourier Transform of the input waveform (i.e. represent it as the sum of a set of sine waves calculated appropriately). Consider any one of these sine waves by itself. The output of an integrator that has a sine wave as its input is a cosine wave of the same frequency. A sine wave is uncorrelated with a cosine wave of the same frequency. Since no two of the input sine waves are correlated, no two of the corresponding integrator output cosine waves are correlated. Since all the cosine wave outputs are uncorrelated with the corresponding input sine waves, their sum, which is the output waveform, is uncorrelated with the sum of the input waves, which is the input waveform.
Martin
–
Richard S. Marken
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
–Antoine de Saint-Exupery
–
Richard S. Marken
"Perfection is achieved not when you have nothing more to add, but when you
have nothing left to take away.�
–Antoine de Saint-Exupery