
···
[Martin Taylor
2013.01.01.12.40]
As you can see by the date stamp, I started this on New Year's
Day, expecting it to be quite short and to be finished that day.
I was wrong on both counts.
This message is a follow-up to [Martin Taylor 2012.12.08.11.32]
and the precursor of what I hope will be messages more suited to
Richard Kennaway’s wish for a mathematical discussion of
information in control. It is intended as part 1 of 2. Part 1
deals with the concepts and algebra of uncertainty, information,
and mutual information. Part 2 applies the concepts to control.
Since writing [Martin Taylor 2012.12.08.11.32], which showed the
close link between control and measurement, and followed the
information “flow” around the loop for a particular control
system, I have been trying to write a tutorial message that
would offer a mathematically accurate description of the general
case while being intuitively clear about what is going on. Each
of four rewrites from scratch has become long, full of
equations, and hardly intuitive to anyone not well versed in
information theory. So now I am trying to separate the
objectives. This message attempts to make information-theoretic
concepts more intuitive with few equations beyond the basic ones
that provide definitions. It is nevertheless very long, but I
have avoided most equations in an attempt to make the principles
intelligible. I hope it can be easily followed, and that it is
worth reading carefully.
My hope is that introducing these concepts with no reference to
control will make it easier to follow the arguments in later
messages that will apply the concepts and the few equations to
control.
This tutorial message has several sections, as follows:
Basic background
concepts
definitions
uncertainty
comments on "uncertainty"
information
Information as change in uncertainty
mutual information
Time and rate
Uncertainty
Information
Information and history
Some worked out example cases
1. A sequence like "ababababa..."
2. A sequence like "abacacabacababacab...."
3. A sequence in which neighbour is likely to follow
neighbour
4. A perfect adder to which the successive input values are
independend
5. A perfect adder to which the successive input values are
not independent
6. Same as (5) except that there is a gap in the history –
the most recent N input samples are unknown.
[Because I don't know whether subscripts or Greek will come out
in everyone’s mail reader, I use “_i” for subscript “i”, and
Sum_i for “Sum over i”. "p(v)’ means “the probability of v being
the case”, so p(x_i) means "the probability X is in state i"and
p_x_i(v) means “the probability that v is the case, given that x
is in state i”, which can also be written p(v|x_i).]
------------Basic equations and concepts: definitions-------
1. "Probability" and "Uncertainty"
In information theory analysis, "uncertainty" has a precise
meaning, which overlaps the everyday meaning in much the same
way as the meaning of “perception” in PCT overlaps the everyday
meaning of that word. In everyday language, one is uncertain
about something if one has some idea about its possible states
– for example the weather might be sunny, cloudy, rainy, snowy,
hot, … – but does not know in which of these states the
weather is, was, or will be now or at some other time of
interest. One may be uncertain about which Pope Gregory
instituted the Gregorian calendar, while feeling it more likely
that it was Gregory VII or VIII than that it was Gregory I or
II. One may be uncertain whether tomorrow’s Dow will be up or
down, while believing strongly that one of these is more
probable than that the market will be closed because of some
disaster.
If one knows nothing about the possibilities for the thing in
question (for example, “how high is the gelmorphyry of the
seventh frachillistator at the winter solstice?”) one seldom
thinks of oneself as “uncertain” about it. More probably, one
thinks of oneself as “ignorant” about it. However, “ignorance”
can be considered as one extreme of uncertainty, with
“certainty” as the other extreme. “Ignorance” could be seen as
“infinite uncertainty”, while “certainty” is “zero uncertainty”.
Neither extreme condition is exactly true of anything we
normally encounter, though sometimes we can come pretty close.
Usually, when one is uncertain about something, one has an idea
which states are more likely to be the case and which are
unlikely. For example, next July 1 in Berlin the weather is
unlikely to be snowy, and likely to be hot, and it is fairly
likely to be wet. It is rather unlikely that the Pope is
secretly married. It is very likely that the Apollo program
landed men on the moon and brought them home. One assigns
relative probabilities to the different possible states. These
probabilities may not be numerically exact, or consciously
considered as numbers, but if you were asked if you would take a
5:1 bet on it snowing in Berlin next July 1 (you pay $5 if it
does snow and receive $1 if it doesn’t snow), you would probably
take the bet. If you would take the bet, your probability for it
to snow is below 0.2.
Whether "uncertainty" is subjective or objective depends on how
you treat probability. If you think of probability as a limit of
the proportion of times one thing happens out of the number of
times it might have happened, then for you, uncertainty is
likely to be an objective measure. I do not accept that approach
to probability, for many reasons on which I will not waste space
in this message. For me, “probability” is a subjective measure,
and is always conditional on some other fact, so that there
really is no absolute probability of X being in state “i”.
Typically, for the kind of things of interest here, when the
frequentist “objective” version is applicable, the two versions
of probability converge to the same value or very close to the
same value. Indeed, subjective probability may be quite strongly
influenced by how often we experience one outcome or another in
what we take to be “the same” conditions. In other cases, such
as coin tossing, we may never have actually counted how many
heads or tails have come up in our experience, but the shape of
the coin and the mechanics of tossing make it unlikely that
either side will predominate, so our subjective probability is
likely to be close to 0.5 for both “heads” and “tails”. As
always, there are conditionals: the coin is fair, the coin
tosser is not skilled in making it fall the way she wants, it
does not land and stay on edge, and so forth.
In order to understand the mathematics of information and
uncertainty, there is no need to go into the deep philosophical
issues that underlie the concept of probability. All that is
necessary is that however probabilities are determined, if you
have a set of mutually exclusive states of something, and those
states together cover all the possible states, their
probabilities must sum to 1.0 exactly. Sometimes inclusivity is
achieved by including a state labelled “something else” or
“miscellaneous”, but this can be accommodated. If the states
form a continuum, as they would if you were to measure the
height of a person, probabilities are replaced by probability
density and the sum by an integral. The integral over all
possibilities must still sum to 1.0 exactly.
-------definitions-----
First, a couple of notations for the equations I do have to use:
I use underbar to mean subscript, as in x_i for x subscript i.
p(x_i) by itself means "Given what we know of X, this is the
probability for us that X is (was, will be) in state i" or, if
you are a frequentist, “Over the long term, the proportion of
the times that X will be (was) in state i is p(x_i)”.
I mostly use capital letters (X) to represent systems of
possible states and the corresponding lower-case letters to
represent individual states (x for a particular but unspecified
state, x_i for the i’th state).
p(x_i|A) means "If A is true, then this is our probability that
X is in state i" or “Over the long term, when A is true, the
proportion of the time that X will be in state i is p(x_i)”. In
typeset text, sometimes this is notated in a more awkward way,
using A as a subscript, which I would have to write as p_A(x_i).
I will not make any significant distinction between the
subjective and objective approaches to probability, but will
often use one or the other form of wording interchangeably (such
as “if we know the state of X, then …”, which you can equally
read as “If X is in a specific state, then …”). Depending on
which approach you like, “probability”, and hence “uncertainty”,
is either subjective or objective. It is the reader’s choice.
I use three main capital letter symbols apart from the Xs and Ys
that represent different systems. U( ) means “Uncertainty”, I( )
means Information, and M( : ) means mutual information between
whatever is symbolized on the two sides of the colon mark. The
parentheses should make it clear when, say, “U” means a system U
with states u_i and when it means “Uncertainty”.
-----definition of "uncertainty"----
If there is a system X, which could be a variable, a collection
of possibilities, or the like, that can be in distinguishable
states x_i, with probabilities p(x_i), the uncertainty of X is _defined _
by two formulae, one applicable to discrete collections or
variables
U(X) = - Sum_i (p(x_i) log(p(x_i)))
the other for the case in which "i" is a continuous variable. If
“i” is continuous, p(x_i) becomes a probability density and the
sum becomes an integral
U(X) = - Integral_i (p(x_i) log(p(x_i)) di).
That's it. No more, no less. Those two equations define
“uncertainty” in the discrete and the continuous case.
(Aside: Von Neumann persuaded Shannon to stop calling U(X)
“uncertainty” and to call it “Entropy” because the equations are
the same. This renaming was unfortunate, as it has caused
confusion between the concepts of uncertainty and entropy ever
since.)
If X is a continuous variable, the measure of uncertainty
depends on the choice of unit for “i”. If, for example, X has a
Gaussian distribution with standard deviation s, and we write H
for log(sqrt(2PIe)), the uncertainty of X is H + log(s). The
standard deviation is measured in whatever units are convenient,
so the absolute measure of uncertainty is undetermined. But
whatever the unit of measure, if the standard deviation is
doubled, the uncertainty is increased by 1 bit. Since we usually
are concerned not with the absolute uncertainty of a system, but
with changes in uncertainty as a consequence of some observation
or event, the calculations give well-defined results regardless
of the unit of measure. When the absolute uncertainty is of
interest, one convenient unit of measure is the resolution limit
of the measuring or observing instrument, since this determines
how much information can be obtained by measurement or
observation.
There are a few other technical issues with the uncertainty of
continuous variables, but calculations using uncertainty work
out pretty much the same whether the variable is discrete or
continuous. Unless it matters, in what follows I will not
distinguish between discrete and continuous variables.
--------comments on "uncertainty-----
Why is Sum(p*log(p)) a natural measure of "uncertainty"?
Shannon, in his 1947 monograph that introduced information
theory to the wider world, proved that this is the only function
that satisfies three natural criteria:
(1) When the probabilities vary continuously, the uncertainty
should also vary continuously.
(2) The uncertainty should be a maximum when all the
possibilities are equally probable.
(3) If the set is partitioned into two subsets, the uncertainty
of the whole should be the weighted sum of the uncertainties of
the two parts, the weights being the total probabilities of the
individual parts. Saying this in the form of an equation, if X
has possibilities x_1, x_2, … x_n and they are collected into
two sets X1 and X2, then
U(X) = p(X1)*U(X1) + p(X2)*U(X2),
where p(Xk) is the sum of the probabilities of the possibilities
collected into set Xk.
One important consequence of the defining equation U(X) =
Sum_i(p(x_i)*log(p(x_i))) is that the uncertainty U(X) is always
positive and ranges between zero (when one of the p(x_i) is 1.0
and the rest are zero) and log(N) (when there are N equally
probable states of X). The logarithm can be to any base, but
base 2 is conventionally used. When base 2 is used, the
uncertainty is measured in “bits”. The reason for using base 2
is convenience. If you can determine the actual state through a
series of yes-no questions to which every answer is equally
likely to be yes or no, the uncertainty in bits is given by the
number of questions.
I will use the term "global uncertainty of X" for the case when
nothing is assumed or known about X other than its long-term
probability distribution over its possible states. This is what
is meant by “U(X)” in what follows, unless some other
conditional is specified in words.
In certain contexts, uncertainty is a conserved quantity. For
example, if X and Y are independent, the joint uncertainty of X
and Y, symbolised as U(X,Y), is
U(X,Y) = U(X) + U(Y)
where U(X,Y) is the uncertainty obtained from the defining
equation if each possible combination of X state and Y state
(x_i, y_j) is taken to be a state of the combined system. The
concept can be extended to any number of independent variables:
U(X, Y, Z, W....) = U(X) + U(Y) + U(Z) + U(W) +...
Using the subjective approach to probability, "independent"
means “independent given what is so far known”. It is not clear
how the term can legitimately be used in a frequentist sense,
because any finite sample will show some apparent relationships
among the systems, even if an infinite set of hypothetical
trials would theoretically reduce the apparent relationships to
zero. A frequentist might say that there is no mechanism that
connects the two systems, which means they must be independent.
However, to take that into account is to concede the
subjectivist position, since the frequentist is saying that *** as
far as he knows*** , there is no mechanism. Even if
there was a mechanism, to consider it would lead the frequentist
into the subjectivist heresy.
Uncertainty is always "about" something. It involves the
probabilities of the different states of some system X, and
probabilities mean nothing from inside the system in question.
They are about X as seen from some other place or time. To say
this is equivalent to saying that all probabilities are
conditional. They depend on some kind of prior assumption, and
taking a viewpoint is one such assumption.
Consider this example, to which I will return later: Joe half
expects that Bob will want a meeting, but does not know when or
where that is to be if it happens at all. What is Joe’s
uncertainty about the meeting?
Joe thinks it 50-50 that Bob will want a meeting. p(meeting) =
0.5
If there is to be a meeting, Joe thinks it might be at Joe's
office or at Bob’s office, again with a 50-50 chance.
If there is to be a meeting, Joe expects it to be scheduled for
some exact hour, 10, 11, 2, or 3.
For Joe, these considerations lead to several mutually exclusive
possibilities:
No meeting, p=0.5
Bob's office, p = p(meeting)*p(Bob's office | meeting) = 0.5*0.5
= 0.25
Joe's office p = p(meeting)*p(Joe's office | meeting) = 0.5*0.5
= 0.25
Joe has 1 bit of uncertainty about whether there is to be a
meeting, and with probability 0.5, another bit about where it is
to be. Overall, his uncertainty about whether and where the
meeting is to be is
U(if, where) = -0.5log(0.5) - 2*(0.25log(0.25) = -0.5*(-1) -
0.5*(-2) = 1.5 bits
no meeting meeting&&either
office
Another way to get the same result is to use a pattern that will
turn up quite often
U(if, where) = U(if) + U(where|if) = U(if) + p(no
meeting)U(where|no meeting) + p(meeting)U(where|meeting) = 1 +
0.50+0.51 = 1.5 bits
Joe is also uncertain about the time of the meeting, if there is
one. It could be at 10, 11, 2, 3 regardless of where the meeting
is to be. That represents 2 bits of uncertainty, but those two
bits apply only if there is to be a meeting.
U(time|meeting) = 2 bits
U(time) = U(time)*p(meeting) + U(time)*p(no meeting) = 0.5*2 +
0.5*0 = 1.
U(if, where, time) = 2.5 bits
Compare this with Joe's uncertainty about the meeting if he knew
there would be a meeting, but did not know whether it included
Alice. Then we would have three mutually independent things Joe
would be uncertainty about:
U(Alice) = 1 bit
U(office) = 1 bit
U(time) = 2 bits
Joe's uncertainty about the meeting would be 4 bits.
Notice what happened here. We added a dimension of possible
variation independent of the dimensions we had already, but
eliminated the dimension of whether there would be a meeting.
That dimension (“if”) interacted with the other two, because if
there was to be no meeting, there could be no uncertainty about
its time and place. Adding an independent dimension of variation
adds to the uncertainty; it does not multiply the uncertainty.
U(meeting_configuration) = U(Alice) + U(office) + U(time)
------
2. "Information" and related concepts
"Information" always means change in uncertainty. It is a
differential quantity, whereas “uncertainty” is an absolute
quantity. I(X) = delta(U(X)).
A change in the uncertainty about X may be because of the
introduction of some fact such as the value of a related
variable, or because of some event that changes the probability
distribution over the states of X. If it is sunny today, it is
more likely to be sunny tomorrow than if today had happened to
be rainy.
To continue the "meeting" example, imagine that Joe received a
call from Bob saying that the meeting was on and in his office,
but not specifying the time. Joe’s uncertainty would be 2 bits
after the phone call, but was 2.5 bits before the call. He would
have gained 0.5 bit of information about the meeting. If the
call had said the meeting was off, Joe would have no further
uncertainty about it, and would have gained 2.5 bits. His
expected gain from a call about whether the meeting was off or
on, and its location if it was on, would be 0.50.5 + 0.52.5 =
1.5 bits, which is the uncertainty we computed by a different
route above for U(if, where).
Often the "event" is an observation. If you observe a variable
quantity whose value you did not know exactly, your uncertainty
about it is likely (but not guaranteed) to be lower after the
observation than before. Again, thinking of Joe’s meeting, if
the call had simply told Joe the meeting was on, without
specifying the location, Joe’s uncertainty about the meeting
would have increased from 1.5 bits to 3 bits (1 bit for where
the meeting is to be held and 2 bits for when). In that case his
information gain would have been negative. However, averaged
over all the possible messages and taking account of their
probabilities, the information gain from a message or
observation is always zero or positive, even though there may be
individual occasions when it is negative.
The information gained about X from an observation is:
I_observation(X) = U_before-observation(X) -
U_after-observation(X)
---------
Mutual Information
The Mutual information between X and Y is the reduction in the
joint uncertainty of two systems X and Y due to the fact that X
and Y are related, which means that knowledge of the state of
one reduces uncertainty about the state of the other. If the
value of Y is observed, even imprecisely, more is known about X
than before the observation of Y.
When two variables are correlated, fixing the value of one may
reduce the variance of the other. Likewise, we define “mutual
information” as the amount by which uncertainty of one is
reduced by knowledge of the state of the other. If U(X|Y) means
the uncertainty of X when you know the value of Y, averaged over
all the possible values of Y according to their probability
distribution, then the mutual information between X and Y is
M(X:Y) = M(Y:X) = U(X) - U(X|Y) = U(Y) - U(Y|X)
Here is another generic equation for mutual information, using
the reduction in the joint uncertainty of the two systema as
compared to the sum of their uncertainties:
M(X:Y) = U(X) + U(Y) - U(X,Y)
from which it is obvious that M(X:Y) = M(Y:X) and that M(X:Y)
cannot exceed the lesser of the two uncertainties U(X) and U(Y).
If X is a single-valued function of Y (meaning that if you know
the value of Y, you can thereby know the value of X) then M(X:Y)
= U(X).
M(X:Y) is always positive, though there may be specific values
of one of the variables for which the uncertainty of the other
is increased over its average value, as happened when Joe was
told the meeting was on without being told were, when, or who
was attending.
Going back again to Joe's office meeting, suppose Joe knows
there is to be a meeting, but does not know where or when. It
might be at Bob’s office or at Bob’s house. If it is at the
office, it might be at 10 or at 2. If at the house, it might be
at 6 (with a dinner invitation) or at 9 (after dinner).
U(where) = 1 bit
U(when) = 2 bits
U(when) + U(where) = 3 bits
But U(when, where) is not 3 bits, because there are actually
only four equiprobable combinations of place and time, 10 and 2
at the office, 6 and 9 at the house, so U(where, when) = 2 bits.
Therefore M(where:when) = 1 bit.
-----time and rates----
Since "information" is a difference quantity, the concept of
“information rate” becomes useful. It is the rate at which
uncertainty changes as a result of ongoing conditions or events.
Consider I(X|observation), the information gained about X as the
result of an observation. Imagine that a series of observations
are made at regular intervals. if X does not change state over
time, then each successive observation is likely to further
reduce U(X). Because of the definition of “information” as
“change in uncertainty”, the observer gains information at a
rate that is the average reduction in uncertainty per
observation divided by the time between observations.
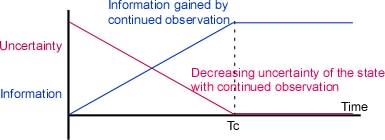
If X is a discrete system, there is a limit to how much
information can be gained about X by observing it. If the global
uncertainty of X (what you believe about X before observing it)
is U(X), no amount of observation can reduce that uncertainty
below zero – the value of U(X) when you know the state of X
exactly. Accordingly, the information gained by continued
observation of a static quantity plateaus at the global
uncertainty of that variable – the amount that the observer did
not know about it before starting the series of observations.
(Figure 1)
This is one place where the difference between continuous and
discrete variables matters. If the system X has a finite number,
N, of distinguishable states, its uncertainty cannot be greater
than log(N), so log(N) is the maximum amount of information that
could be obtained about it by continued or repeated observation.
But if the states of X form a continuum, it has an infinite
number of states, meaning that in theory there is no limit to
the amount of information about it that could be gained by
continued observation. In practice, of course, the resolution of
the observing system imposes a limit. Precision is never
infinite, even if the limit is imposed by quantum uncertainty.
What about the situation in which X is or may be changing? If a
changing X is observed once, the uncertainty about X becomes a
function of time since the observation. X may change state
continuously or abruptly, slowly or fast. However it may change,
the “information rate” of X is defined as dU(X)/dt provided that
the observation timing is independent of anything related to a
particular state or state change of X.
-----------
[Aside: Here we have another example of the kind of
complementarity between two measures that is at the heart of the
Heisenberg Uncertainty Principle of quantum mechanics. If you
know exactly where something is, you know nothing about its
velocity, and vice versa. The rate at which you get information
from observing something can tell you about both its value and
the rate of change of value, but the more closely define one of
these, the less you can know about the other. The information
rate determines the size of the “precision*velocity” cell.]
-----------
If an observation is made at time t0 and never thereafter,
immediately after the observation at time t0+e (“e” represents
“epsilon”, a vanishingly small quantity) the uncertainty of X is
U_(t0+e)(X) . From that moment, U_t(X) increases over time. The
rate at which U_t(X) increases depends, in the casual
tautological sense, on how fast the value of X changes. If the
variable is a waveform of bandwidth W, this can be made a bit
more precise. The actual rate depends on the spectrum of the
waveform, but for a white noise (the worst case) the rate dU/dt
= Wlog(2pieN) where N is the noise power (which again
depends on the choice of units).
However, just as continued observation cannot yield more
information than the initial uncertainty of X, so continued
external influences or other cause of variation cannot increase
U_t(X) beyond its global value (its value determined from the
long-term statistics of X).
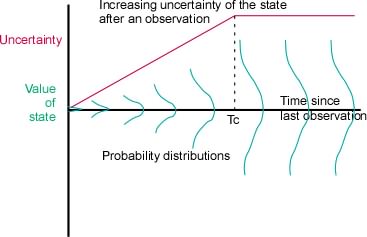
(Figure 2)
----------
3. Information and history
In this section, we are interested in the mutual information
between the preceding history and the following observation,
which is symbolized M(X|Xhistory). In everyday language, we want
to know how much we can and cannot know about what we will
observe from what we have observed.
Mutual information need not be just between the states of system
X and the states of a different system Y. It can be between the
states of system X at two different times, which we can call t0
and t1. If t0 and t1 are well separated, the state of X at time
t0 tells you nothing about its state at time t1. This would be
the case at any time after Tc in Figure 2. But if t1 follows t0
very closely (i.e. near the left axis in Figure 2), it is very
probable that the state of X has not changed very much, meaning
that the Mutual Information between the two states is large.
They are highly redundant, which is another way of saying that
the mutual information between two things is close to its
maximum possible value.
Suppose X is the weather. If it is sunny at 10 o'clock, it is
likely to be sunny at one second past ten, or one minute past
ten. The probability of it remaining sunny is still pretty high
at 11, and still moderately high at ten tomorrow. But by this
time next week, the observation that it is sunny now will not
tell you very much more about whether it will be sunny then than
will a book about the local climate at this time of year.
As the example suggests, M(X_t:X_(t-tau)) -- the complement of
U_(t-tau)(X|observation at t0) shown in Figure 2-- is a function
of tau that usually decreases with increasing tau. I say
“usually”, because it is not true of periodic or nearly periodic
systems. The temperature today is likely to be nearer the
temperature this time last year than to the temperature at some
randomly chosen date through the year. For now we will ignore
such cyclic variation, and treat M(X_t:X_(t-tau)) as if it
declined with increasing tau, until, at some value of tau, it
reaches zero.
------footnote-------
For a signal of bandwidth W, M(X_t:X_(t-tau)) reaches zero at
tau = 1/2W. No physical signal is absolutely restricted to a
precisely defined bandwidth, but the approximation can be pretty
close in some cases. Good audio sampling is much faster than
1/2W because the physical signals of musical instruments have
appreciable power at frequencies well about the listener’s
hearing bandwidth.
-----end footnote-----
Suppose a signal is sampled at regular intervals separated by
tau seconds, with tau small enough that knowledge of the signal
value at one sample reduces the uncertainty of the state of the
next and previous samples. The probability distribution of the
next sample is constrained by the values of the previous
samples. One might think of the value of the sample as being
that of a perception, but that is not necessary.
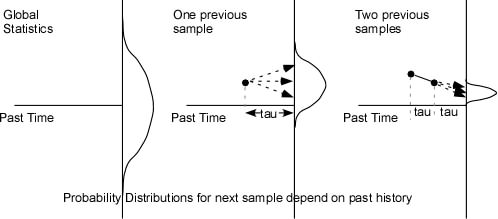
(Figure 2)
Figure 2 suggests how knowledge of the past values may constrain
the probability distribution of the next sample value when the
inter-sample time, tau, is short compared to the rate of change
of the variable.
The first panel suggests the uncertainty of the next sample if
one knows nothing of the history of the variable. If the
variable is from the set of possible states of X, its
uncertainty is U(X). The second and third panels show how the
uncertainty is reduced if the values of the previous one or two
samples are known. In the middle panel, one possible value of
the previous sample is shown, and in the third panel the values
of the two previous samples are taken into account.
The figure is drawn to show the changes in a slowly changing
waveform, but that is just one possibility. It could equally
easily represent the probabilities in a sequence of letters in a
text. For example, the left panel might represent the
possibility of observing any letter of the alphabet, the middle
the distribution of the next character after observing a “t”,
and the right panel the distribution of the following character
after observing “th”. Since we assume that the statistics of X
are stationary (i.e. do not depend on when you sample them,
provided that choice of the sampling moment is independent of
anything happening in X), M(X0:X1) = M(X1:X2) = M(X2:X3)…
We want to know the uncertainty of X at a given moment t0 given
its entire previous history. If X is a slowly varying waveform,
its uncertainty knowing the previous history right up to t0 is
zero, which is uninteresting. In that case we have to ask about
its history only up to some time t0-tau. We will actually
consider the history to consist of successive samples separated
by tau seconds. In the case of a discrete system such as the
letters of a text, no such restriction is required, but by
making the restriction on the sampling of the continuous
waveform we can treat both kinds of system similarly.
Formally, one can write
U(X0|History) = U(X0) - M(X0:History)
but that is not much use unless one can calculate the mutual
information between the next sample value x0 and the history of
system X. It is possible again to write a general formula, but
its actual calculation depends on the sequential statistics of
X.
The History of X can be written as a sequence of samples
counting back from the present: X1, X2, X3, … and
M(X0:History) can be written M(X0:X1, X2, X3,…)
M(X0:History) = M(X0|X1) + M(X0:X2|X1) + M(X0:X3|X2,X1) +
M(X0:X4|X1,X2,X3) + …
In words, the mutual information between the next sample and the
history can be partitioned into the sum of an infinite series of
mutual information elements, each one being the amount one
sample contributes to the total mutual information, given the
specific values of all the samples between it and the most
recent sample.
To make this concrete, let's consider a few specific examples
--------
Example 1: X is a sequence of symbols "a" and "b", that
alternate “…ababab…”
If one looks at an arbitrary moment, one has an 0.5 chance of
the next sample being a or b: U(X0) = 1 bit. If one has seen one
sample, which might have been either a or b, there is no
uncertainty about the next sample: U(X0|X1) = 0, which gives
M(X0:X1) = U(X).
What then of M(X0:X2|X1)? Remember that M(A:B) cannot exceed the
lesser of U(A) and U(B). In this case, U(X2|X1) = 0 because if
X1 was a X2 must have been b, and vice-versa. So M(X0:X2|X1) = 0
and all subsequent members of the series are also zero.
One can extend this example to any series or waveform that is
known to be strictly periodic with a known period.
-------
Example 2: X is a sequence of symbols a, b, and c with the
property that a is followed equally probably by b or c, b by c
or a, and c by a or b. No symbol is ever repeated immediately,
but apart from that, each other symbol is equally likely at any
sample moment.
U(X0) = log(3) = 1.58 bits
U(X0|X1) = 1 bit, which gives
M(X0:X1) = 0.58 bits
It is irrelevant how X1 took on its value from X2. If x1 = a, x2
could have equally well been b or c. Therefore
M(X0:X2|X1) = 0
--------
Example 3. X is a sequence of five different symbols labelled 1,
2, 3, 4, 5. Considering 5 and 1 to be neighbours, each symbol
can be followed by itself with probability 0.5 or one of its
neighbours with probabiity 0.25. Over the long term, each symbol
appears with equal probability.
U(X0) = log(5) = 2.32 bits
U(X0|X1) =-0.5 log 0.5 - 2* (0.25 log 0.25) (because the
probability is 0.5 its predecessor was itself and 0.25 that it
was either of its two neighbours)
= 0.5 + 0.5 = 1 bit
M(X0:X1) = 2.32 - 1 = 1.32 bits
M(X0:X2|X1) depends on the relationship between X2 and X0,
unlike the situation in example 2. There are five possibilities
for x0 (the value of X0). the probability of these five depends
on the relationship between x0 and x2. We must consider each of
these five, and partition M(X0:X1) according to the
probabilities for each value of X2. In a formula:
M(X0:X2|X1) = Sum_k(p(X2=xk)*M(X0:X2|X1=xk))
Since the probability p(X2=xk) is the same for each value of xk
(all symbols are equally likely over the long term), this sum
comes down to
M(X0:X2|X1) = (1/N)*Sum_k(M(X0:X2|X1=xk))
We consider all these possibilities individually. Since all the
relationships are symmetric (meaning that it doesn’t matter
which value we select as the possible next sample, x0), we need
deal only with the relationships themselves.
The sequence could be {x0, x0, x0}, {x0, neighbour, x0}, {x0,
neighbout, neighbour} or {x0, neighbour, non-neighbour}.
Examples of each might be {3.3.3}, {3,4,3}, {3,4,4} and {3,4,5},
which would have probabilities 0.50.5 = 0.25,
20.250.25=0.125, 20.250.5=0,25, and 0.250.25=0.125
respectively.
There is no need to do the actual calculations here. They are
easy but time-consuming. The point is that we can calculate
M(X0:X2), M(X0:X2|X1) and the rest directly from the conditional
probabilities.
---------
Example 4: X is built by summing a succession of samples of
another system Y, such that xj = Sum(History(X)) + yj, x0 = 0
for some specified value of k, and yj is a sequence of positive
and negative integer values, samples from a system Y, that
average zero. In this example, the numbering scheme goes in the
direction of time, later samples being labelled with larger
numbers. At the k’th sample the expression M(X|Xhistory)
becomes
M(Xk:Yk|X_(k-1), X_(k-2), ... X(0))
Each sample of Y contributes equally to the value of X, so there
is no need to consider the sequential order of the y values.
Assuming that Y is a series of numerical values and the samples
of Y are independent, the variance of X increases linearly with
the number of samples, so its standard deviation increases
proportionally to the square root of that number.
Let us trace the contribution of the first few samples of Y to
the uncertainty of X.
After one sample, y0, of Y, x0 will equal y0, which means U(X0)
= U(Y0).
M(X0:Y0) = U(X) + U(Y) - U(X,Y) = U(X) = U(Y)
After the next sample, U(X1) still is given by the formula Sum(p
log p), but the probabilities are no longer the same as they
were before the first sample. There is a wider range of
possibilities, from twice the minimum value of Y to twice the
maximum value of Y, and the probabilities of those possibilities
are not equal. Because the probability distribution over the
possible values of X is not uniform, U(X) < 2*U(Y).
As more and more samples are included in the Sum, the range of X
increases, but values near zero come to have higher and higher
relative probabilities. The distribution of probabilities over
the possible values of X approaches a Gaussian with variance
that increases linearly with k, so U(X) approaches U(Y)sqrt(k).
The ratio U(X)/(kU(Y) decreases with increasing k, approaching
1/sqrt(k) as k becomes large .
We want to consider the contribution of the k'th sample of Y.
How much does the kth sample of Y reduce the uncertainty of the
k+1th value of the Sum, as compared to knowing only the History
up to the previous sample? That is the mutual information
between the kth sample of Y and the k+1th value of X.
For large k, (U(X_k) - U(X_(k-1)))/U(Y) approaches
sqrt(k)-sqrt(k-1), an increasingly small number. Yet it remains
true that U(X_k|History) - U(X_k|History, Yk) = U(Y). The
uncertainty of the value of X after the next sample of Y is
always the uncertainty of Y, because if you know the current
value of X, the next value is determined by the value of the Y
sample. How can these two statements be reconciled? The key is
the conditional of knowing the History. Without the prior
History (in this case the Sum), the contribution of each
successive Y sample to the uncertainty of X becomes less and
less, but if you do have the prior History, the value of the
next X sample will have an uncertainty that is the uncertainty
of the Y sample.
The situation is the same if the system X is normalized, meaning
that its variance is independent of the number of prior samples
after a sufficient number of Y values have occurred. The
magnitude of the contribution of the k’th Y sample is reduced
proportionally to sqrt(k), but its contribution to the various
uncertainties are the same, provided that the different possible
values of X are resolved.
--------
Example 5: The same as Example 4 except that the samples of Y
are not independent. If Y is a continuous waveform, the samples
are taken more closely than the Nyquist limit (samples separated
by 1/2W, where W is the bandwidth of the waveform). If Y is a
discrete set of possibilities, successive samples are related by
some kind of grammar. The two kinds of possibility converge when
the discrete set of possibilities is linearly arranged and the
grammar merely makes transitions among nearby values more likely
than across distant values.
The new issue here is that if the history of Y is known, U(Yk)
< U(Y). Therefore M(Xk:History(X), yk) < U(Y). Each
successive sample of Y reduces the uncertainty of X less than
would be the case if the samples of Y were independent of each
other. The difference is subsumed by the fact that
M(Xk|History(X)) is greater than it is in the case when the Y
samples are independent, by the same amount.
---------
Example 6: System X is a function of the current and past
samples of system Y. We want to know the uncertainty of sample
xk when the values of successive Y samples are known only up to
sample y_(k-h). For example, in the grammar of example 3, we may
have observed the sequence 1,2,1,5, (samples y1, y2, y3, y4) and
want to know the uncertainty of sample x6, which is a function
of y1, y2, y3, y4, y5, and y6. We do not yet know the values of
y5 or y6. As a real-world example, a trader in the days of
sailing ships might have known the market conditions in China
and England several months before his ship captain actually
bargains for tea in Canton, but the earlier conditions are the
conditions on which he must base his instructions to the
captain.
[Martin Taylor 2012.12.08.11.32]
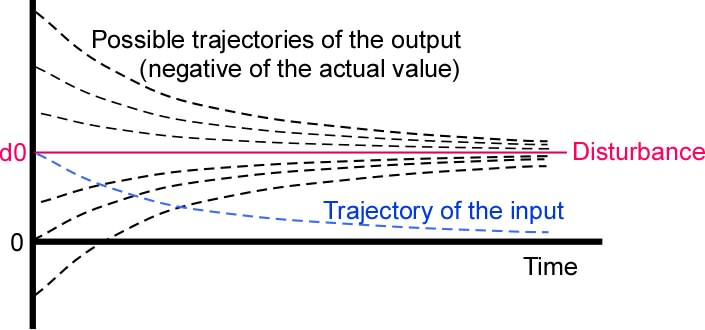
.... We consider the "basic-standard" control system that has a pureintegrator as its output function.
First, let's treat the effect of one step change in thedisturbance value. We assume that the error is initially zero,
and at time t0 the disturbance suddenly goes from whatever value
it may have had previously to d0. We treat this single step, and
then consider the effects of a series of steps. We start by
showing how the integrator rate parameter controls how fast
information about the disturbance arrives at the output – how
fast the control system measures the disturbance value.Let us trace the signal values at various places in the loop astime passes after the step at time t0. At time t0+e (e means
epsilon, an indefinitely small amount), the error value is -d
and the output value qo is zero. At this early time the output
value is whatever it was before the step, and has an unchanged
influence on the value of the input quantity qi. As time passes,
the output value changes exponentially until after infinite time
it reaches -d. Assuming q0 was initially zero, then at time t:qo(t) = -d0*(1-e^(-G*(t-t0))). At the same time, the input value qi approaches zero by the sameexponential:
qi(t) = 1 - e^(-G*(t-t0)) Exponential changes in value are quite interesting ininformation theory, as they often indicate a constant bit rate
of information transfer. To see this, you must understand that
although the absolute uncertainty about the value of a
continuous variable either before or after a measurement or
observation is always infinity, the information gained through
the measurement or observation is finite. If the range of
uncertainty about the value (such as standard deviation of
measurement) is r0 before the measure and r1 after the measure,
the information gained is log2(r0/r1) bits.Measurements and observations are never infinitely precise. Whensomeone says their perception is subjectively noise-free and
precise, they nevertheless would be unable to tell by eye if an
object changed location by a nanometer or declined in brightness
by one part in a billion. There is always some limit to the
resolution of any observation, so the issue of there being an
infinite uncertainty about the value of a continuous variable is
never a problem. In any case in which a problem of infinite
uncertainty might seem to be presenting itself, the solution is
usually to look at the problem from a different angle, but if
that is not possible it is always possible to presume a
resolution limit, a limit that might be several orders of
magnitude more precise than any physically realizable limit, but
a limit nevertheless.(If you want to get a more accurate statement, and see thederivation of all this, I suggest you get Shannon’s book from
Amazon at the link I provided earlier ).
In the above example, q0 could have started at any value
whatever, and would still have approached -d exponentially with
the same time constant. The output value qo has the character of
a continuous measurement of the value of the disturbance, and
this measurement gains precision at a rate given by
e^(-G*(t-t0)). (The units of G are 1/seconds).
What is this rate of gain in precision, in bits/sec? One bit of
information has been gained when the uncertainty about the value
of d0 has been halved. In other words, the output has gained one
bit of information about the disturbance by the time tx such
that
e^(-G*(tx-t0)) = 0.5
Taking logarithms (base 2) of both sides, we have
log2(e)(-G(tx-t0)) = -1
tx-t0 = 1/(Glog2(e)) = 1/(G1.443…) seconds
That is the time it takes for q0 to halve its distance to its
final value -d0 no matter what its starting value might have
been, which means it has gained one bit of information about the
value of the disturbance. The bit rate is therefore G1.443…
bits/sec. That is the rate at which the output quantity q0 gains
information about the disturbance, and also is the rate at which
the input quantity loses information about the disturbance. The
input quantity must lose information about the disturbance,
because it always approaches the reference value, no matter what
the value of the disturbance step. I suppose you could look upon G1.443 as the bit rate of the
loop considered as a communication channel, but it is probably
not helpful do do so, as the communication is from the input
quantity back to itself. Without the complete loop, q0 does not
act as a measure of d0, but continues negatively increasing
linearly without limit at a rate Gd0. It is better just to
think of G1.443 as the rate at which information from the
disturbance appears at the output quantity.
As a further matter of clarification, I suppose we ought to
mention the behavioural illusion here. If the environmental
feedback path is not a simple connector with a gain of unity,
the output quantity differs from the disturbance value. The
mismatch does not affect the information relationship between
the disturbance and the output quantity, since the environmental
feedback path provides a single-valued environmental feedback
function. It is always possible to compute the influence of the
output on the input quantity if you know the output value q0.
This means that q0 and the influence of the output on the input
quantity are informationally identical, whatever their
functional relationship, providing the environmental feedback
function does not change. If it does change, the effect is
similar to adding a noise source to a communication channel, a
situation that was Shannon’s primary concern and provides no
particular complication to the analysis. (Or in the case of
Marken’s demo that involves switching the sense of the
environmental feedback path, the communication analogy is the
band-switching secret communication procedure patented by the
movie star Hedy Lamarr; in both cases, the switching must be
separately detected or otherwise known).
As a specific example, if the environmental feedback path has a
gain of 2, the output quantity will converge to a value of d/2.
The convergence to d/2 is at the same exponential rate as would
have been the case for en environmental feedback path gain of
1.0, providing an information gain rate that is determined only
by the integration rate parameter G. Information from the
disturbance still arrives at the output quantity (and is lost
from the input quantity) at a rate G1.443… From now on, we will give the label “T” to the rate at which the
output gains information about the disturbance. T = G1.443… bits/sec.
The rate of information gain about the disturbance value at the
output quantity is independent of the disturbance waveform and
of the environmental feedback function. It is a property of the
internal circuitry of the control system. Accordingly, we can
make some estimates about the achievable precision of control
for disturbances that are not simple step functions. First,
however, we should look at the effect of a second and subsequent
step change in the disturbance value.
The disturbance value changed abruptly to d0 at time t0. Now at
time t1 the disturbance value jumps to d1. The input quantity
adds d1-d0 to whatever value it had arrived at by t1. The error
value jumps by the same amount, but the output value qo does not
change immediately, because of the integrator output function.
It starts changing exponentially toward (the negative of) the
new value of the disturbance.
At t1+e, the output quantity has a value that is unknown,
because ever since t0 it has been in the process of approaching
-d0 exponentially from some unknown starting point. The
uncertainty of its current value is T*(t1-t0) bits less than it
had been at time t0, because it was performing a process
functionally equivalent to measuring the value d0. Now it has to
start forgetting the value d0 and start measuring the value d1.
Less colloquially, the mutual information between the output
quantity and the disturbance value is instantly decreased by the
uncertainty of the change in disturbance value, while the mutual
information between the disturbance value and the input value is
increased by the same amount.
By how much are the mutual information values changed by the new
step? Since the absolute uncertainty of a continuous variable is
infinite, can that change be measured? Shannon shows again that
it can. The amount is log2(r_new/r_old) where r_new is the new
range of uncertainty (such as standard deviation) and r_old is
the old range of uncertainty. The new range of uncertainty
depends on the probability distribution of values that can be
taken by the disturbance at that time, which may be unknown. It
is not a new unknown, however, since the original disturbance
step came from the same distribution, and the original value of
the output quantity probably came from the same distribution
(modified, of course, by the inverse of the environmental
feedback function) if the system had been controlling prior to
the first step that we analyzed.
After the second step change in the disturbance value, the
output quantity is gaining information, still about the
disturbance value, but not about d0. Now it is gaining
information about d1 and losing information about d0. At the
same time, the input quantity is losing information about d1, as
well as about any remanent information about d0 that might still
have been there at time t1. All this is happening at a rate of T
= G*1.44.3… bits/sec.
The effects of third and subsequent steps in the value of the
disturbance are the same. The output continues to gain
information about the most recent value of the disturbance at T
bits/sec while losing information about prior values at the same
rate, and while the input also loses information about the new
and old values at T bits/sec. Making the steps smaller and
closer in time, we can approximate a smooth waveform with any
desired degree of precision. No matter what the disturbance
waveform, the output is still getting information about its
value at T bits/sec, and losing information about its history at
the same rate. So long as the disturbance variation produces less than T
bits/sec, control is possible, but if the disturbance variation
is greater than T bits/sec, control is lost. The spike in the
input value at a step change in the disturbance is an example of
that, where control is completely lost at the moment of the
step, and gradually regained in the period when the disturbance
remains steady, not generating uncertainty.This is getting rather too long for a single message, so I will
stop there. I hope it explains just how information gets from
the disturbance to the output, and how fast it does so in the
case of the ideal noiseless control system with no lag and a
pure integrator output function.
Martin
http://www.amazon.com/Mathematical-Theory-Communication-Claude-Shannon/dp/0252725484/ref=sr_1_1?s=books&ie=UTF8&qid=1354736909&sr=1-1&keywords=Shannon%2C+C.+E.