I am loving this, and Bill’s acute use of language and clear frustration with the science that is out there.
So much for considering Ashby and Powers idea to be similar eh Boris?
Here’s another gaggle of myths, this time from W. Ross Ashby, in _An Introduction to Cybernetics (New York: Wiley, 1966 (third printing, copyright 1963).
The basic formulation of s.11/4 assumed that the process of regulation went through its successive stages in the following order:
1.A particular disturbance threatens at D;
2.it acts on R, which transforms it to a response;
3.the two values, of D and R, act on T simultaneously to produce T’s outcome;
4.the outcome is a state of E, or affects E." (p. 221)
E is an essential variable that is to be stabilized by the action of a regulator R, acting through an environmental function T which is fixed. Regulation is achieved when the effect of D on T is precisely cancelled by the response of the regulator R to D, also acting on T. It is assumed that E depends on T and T alone, so there are no disturbances acting directly on E that can’t be sensed by the regulator.
If R and T are precisely calibrated and act with infinite precision, then perfect regulation is possible but not otherwise. Ashby tended to overlook the question of precision, largely because in examples he tended to use small integers or decimal fractions accurate to one decimal place to represent the variables. As a result he greatly overestimated the capacities of compensating systems, and therefore, by comparison, greatly underestimated the capacities of control systems.
Regulation by error. A wellknown regulator that cannot react directly to the original disturbance D is the thermostat controlled water bath, which is unable to say “I see someone coming with a cold flask that is to be immersed in me I must act now.” On the contrary, the regulator gets no information about the disturbance until the temperature of the water (E) actually begins to drop. And the same limitation applies to the other possible disturbances, such as the approach of a patch of sunlight that will warm it, or the leaving open of a door that will bring a draught to cool it." (p. 222).
Note the implication that a compensating regulator might exist which, on seeing someone approach with a flask, could deduce that it contains cold water and is about to be immersed in the bath. Note also the unspoken assumption that merely from qualitative knowledge about a flask of cold water, a patch of sunlight, or a potential draught through an open door, the regulator could be prepared to act quantitatively: to add heat to the bath that would exactly compensate for the cooling from the water in the flask or the evaporation due to the draught, or cooling just sufficient to prevent any rise in the temperature of the bath. From qualitative knowledge of the disturbance, the regulator somehow achieves exact quantitative compensation for the quantitative effects of the disturbance. If, of course, such a thing were possible, the compensator would be much superior to any form of feedback controller. But such a thing is not remotely possible.
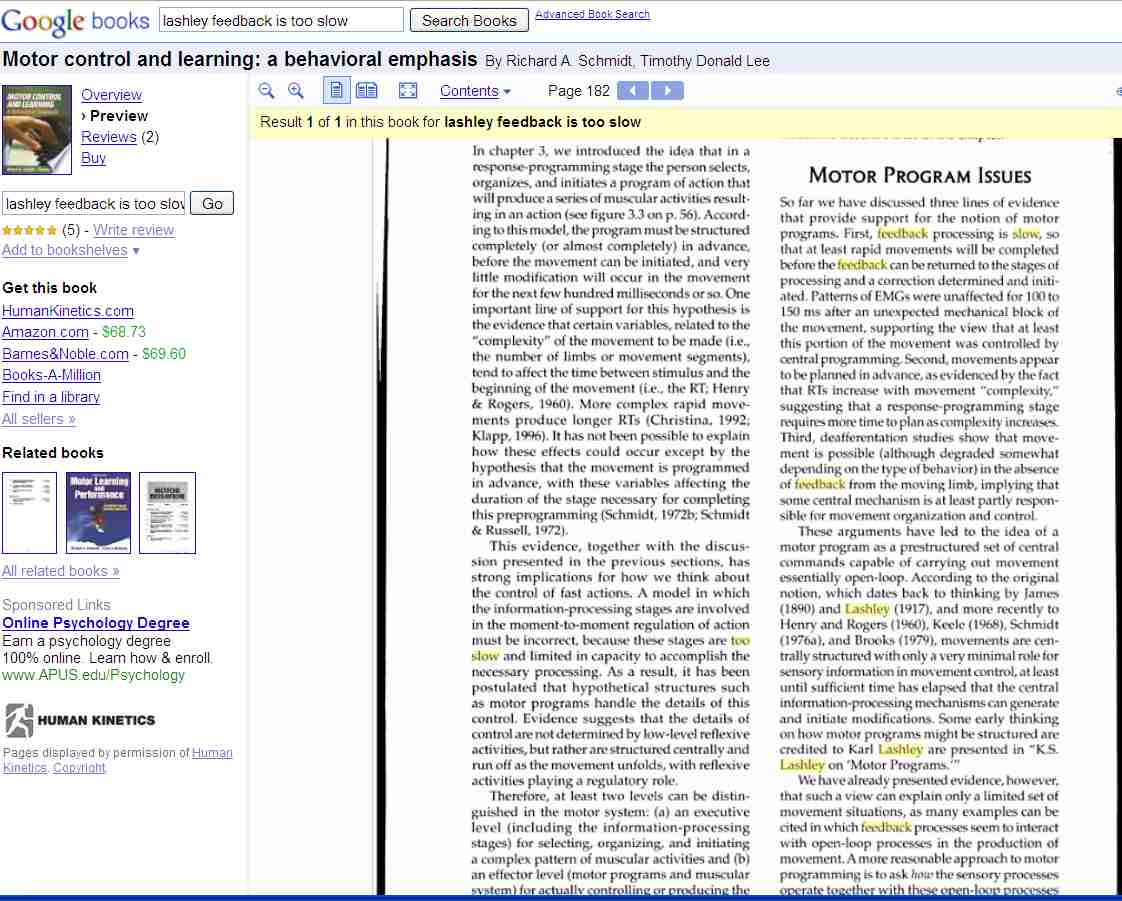
After doing through a series of diagrams, Ashby finally diagrams the true errordriven control system:
… we have the basic form of the simple ‘errorcontrolled servomechanism’ or ‘closedloop regulator,’ with its wellknown feedback from E to R." (p. 223)
The diagram is D > T > E
^ |
R <
Now we get to a whole fountain of misinformation about control systems, a series of deductions that is just close enough to reality to be convincing, and just far enough from it to be utter nonsense.
A fundamental property of the errorcontrolled regulator is that it cannot be perfect in the sense of S.11/3" (p.223)
He then goes through a “formal proof” using the Law of Requisite Variety to conclude
It is easily shown that with these conditions E’s variety will be as large as D’s i.e., R can achieve no regulation, no matter how R is constructed (i.e., no matter what transformation is used to turn E’s value into an Rvalue)."
If the formal proof is not required, a simpler line of reasoning can show why this must be so. As we saw, R gets its information through T and E. Suppose that R is regulating successfully, then this would imply that the variety of E is reduced below that of D perhaps even to zero. This very reduction makes the channel
D > T > E
to have a lessened capacity; if E should be held quite constant then the channel is quite blocked. So the more successful R is in keeping E constant, the more does R block the channel by which it is receiving its necessary information. Clearly, any success by R can at best be partial." (p. 223224)
This argument has apparently convinced many cyberneticists and others that the Law of Requisite Variety is more general than the principles of control, and in fact shows that control systems are poor second cousins to compensators when it comes to the ability to maintain essential variables constant against disturbance.
In fact this argument shows how utterly useless the Law of Requisite Variety is for reaching any correct conclusion about control systems.
Having swept through this dizzying exercise in proving a falsehood, Ashby then grudgingly allows feedback control to creep humbly back into the picture:
Fortunately, in many cases complete regulation is not necessary. So far, we have rather assumed that the states of the essential variables E were sharply divided into “normal” … and “lethal”, so occurrence of the “undesirable” states was wholly incompatible with regulation. It often happens, however, that the system shows continuity, so that the states of the essential variables lie a long a scale of undesirability. Thus a land animal can pass through many degrees of dehydration before dying of thirst; and a suitable reverse from half way along the scale may justly be called “regulatory” if it saves the animal’s life, though it may not have saved the animal from discomfort. "
Note the gratuitous “half way along the scale.”
Thus the presence of continuity makes possible a regulation that, though not perfect, is of the greatest practical importance. Small errors are allowed to occur; then, by giving their information to R, they make possible a regulation against great errors. This is the basic theory, in terms of communication, of the simple feedback regulator." (p. 224)
The argument then veers off into “Markovian machines” and Markovian stochastic regulation. This is billed as the most important and farreaching application of the errorcontrolled regulator.
Note how the argument relies on qualitative statements to reach quantitative conclusions. It is perfectly true that if a compensating regulator affects T equally and oppositely to the effect of D, E will not be affected at all. But by that same argument, to the extent that R does not have perfect information about D (and about the nature of the connection from D to T and from R to T), T will not be affected equally and oppositely, and thus to the extent of the imperfection, E will not be perfectly regulated. Furthermore, if there is any disturbance at all that is NOT detected by R (for example, a disturbance that acts directly on E), the effects of that disturbance will not be compensated at all. If R does not compensate for all nonlinearities and timefunctions in the connection from D to T, compensation will not occur. When the processes involved are thought of as real physical processes in a real environment, the idealized assumptions behind the compensatory regulator are easily seen to be unrealistic they predict regulation that is far, far better than any that could actually be achieved in this way.
Note also how the qualitative concept that errorregulated control must be imperfect is used to imply that it must be more imperfect than compensatory regulation. This non sequitur has appeared in the literature over and over ever since Ashby. In his earlier book Ashby was still toying with true feedback control and continuous systems; the appendix is heaped with rather aimless mathematics that is oriented in that direction. But in this second book, Ashby shows that he never understood how an “errorcontrolled” regulator works. He didn’t know that the “imperfection” inherent in such systems can be reduced to levels of error far smaller than the errorreductions that any real compensating system could achieve smaller by orders of magnitude, in many cases, particularly cases involving human behavioral systems.
Ashby’s entire line of reasoning about feedback control in An introduction to cybernetics is spurious. Yet Ashby has been revered in cybernetics and associated fields for 40 years as a deep thinker and a pioneer. His Law of Requisite Variety has nothing at all useful to say about control systems and in fact led Ashby to a completely false conclusion about them yet it is still cited as a piece of fundamental thinking. Whether Ashby originated these misconceptions or simply picked them up from others I don’t know. One thing is certain: he did not get them from an understanding of the principles of control.
···
On Tue, Apr 22, 2014 at 2:23 PM, rupert@moonsit.co.uk rupert@moonsit.co.uk wrote:
[Rupert Young (2014.04.22 18.00)]
I’ve heard people on here talk about others making this claim as an argument against PCT, and I would like to investigate this further.
Can someone point me to some references of those who have made this claim, and also any refutations that have been made in support of PCT?
Regards,
Rupert