Warren recently uploaded the talk from last year’s IAPCT conference, the first part of the video is Rick Marken’s talk, and the second part is Richard Kennaway, power law and gait planarity. The slides are also available somewhere on the CSGnet. I saw it and wanted to comment and maybe discuss a few things with Richard (in cc)
Some of the things I agree with, I like the conclusion - the first step toward understanding behaviors should be something like the test for the controlled variable, that is how we see what is controlled and get a mathematical definition of the controlled variable. Great.
The power law
I also agree with some of the slides about the power law - lots of movements in the physical world follow some speed-curvature power law - masses on springs, different 2d sinusoids, etc. Lots of smooth periodic functions satisfy the law too. Pure noise also. All good.
The first slide contains some errors:
The voluntary movements produced by people (and other living things) follow a power law
Speed = Curvaturebeta
Lots of movements don’t follow a power law - like movements along straight lines (although some people change the formula, but that is then a different law). For very slow movements where you can maintain constant speed trough any curve, there is also no power law. “Random” movements also don’t consistently produce a power law, but only under certain conditions.
From non-biological movements, you’ve got planets where the speed does not depend on the curvature of the orbit; or a pendulum if you look at it from the side - constant curvature, changing speed, etc, etc.
For the formula, there is generally also a parameter that depends on the average velocity, so the speed is nearly k * curvature beta.
Depending on how speed and curvature are measured, the coefficient, beta, of this power function is always approximately 1/3 or 2/3
This is not correct. Beta is not always approximately 1/3 or 2/3. For different shapes, at high speed, there is a whole range of betas (e.g. Huh and Sejnowski 2015, also reproduced in the reappraisal paper),.
Betas in tracing ellipses also change with speed, but after a point, they converge to 2/3. They change with the drawing medium - tracing ellipses in water is different from tracing them in air, different beta. Small children draw differently than adults, etc, etc.
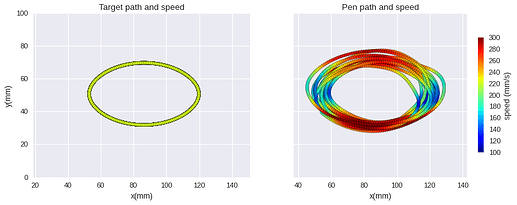
So it is not a very general law, in the sense that the same exponent is appearing everywhere, but it is a very strong law because in the same conditions, drawing the same shape, you get very high correlations, and consistently the same betas . For example, drawing or tracing or tracking ellipses in a smooth and fast way, always produces a speed-curvature law with the same exponent and a high correlation. In other words - people cannot follow constant speed targets along elliptic trajectories with a constant speed - instead they always slow down in the areas of higher curvature, and hurry up a bit in the areas of lower curvature. This is empirical data from one such experiment, I hope the plot and the legends explain everything:
So, my first question is - do you think that the high correlations and consistency of finding the same exponent under the same conditions qualify the speed-curvature power law as a study-worthy behavioral law?
It is not a stimulus-response law, it is simply a feature, or invariance of movement. It is not claimed that the speed is a response to curvature, they are measures of the same instant of behavior. There are some people who theorize that the movement is planned in the brain to achieve the power law but not directly - rather by minimizing different cost functions, like jerk or torque, etc., here are other people who claim otherwise, that the power law is a side effect of some other process, of muscles smoothing the movement, etc. I don’t see nothing new coming from PCT in that debate - planned vs side effect - the solution will probably be in the side effect camp. The new thing will be one or several controlled variables.
In the conclusion on the power law:
Mathematical regularity of power law led researchers to assume that, like Kepler’s laws, it would reveal something about how movements are produced.
Did Kepler’s law reveal something about how planet movements were produced? I think they just described the movements, and then Newton explained them in some sense, with the law of gravitation.
The speed-curvature law is a descriptive law, nothing explanatory, unless, of course, someone explicitly claims that the brain plans the movements to comply with a power law. Generally, people don’t claim this.
PCT-based test for the controlled variable rules out power law as revealing anything about how movement is produced.
I don’t follow this logic. How does the TCV rule out the power law as revealing anything about how movement is produced? I think that a computational model that explains why the power law appears will have to take into account correct controlled variables and a correct ‘body’ element, output function, and then will have to reproduce the power law with the same exponent as the human in the same situation. Or equally, a lack of the power law where it does not appear in human movement.
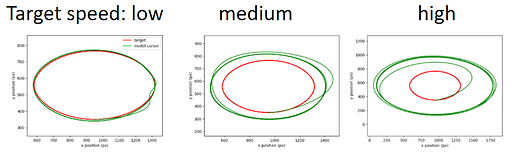
And finally, a standard tracking model (cursor-target distance) does not follow the ellipse in the same way as humans do (target is red, model green):
Interestingly, it does produce a power law trajectory, but the size doesn’t match. So the “simple” model does not really explain much.
For the planarity of movement topic, I also have a comment. In the paper you cite, I can find no claim that the gait planarity is planned. From what I can see they also state it can be emergent from some oscillators as a side effect.