Simulating JUICE (JOOSS) sequence

[Paul]

Hello
I have been simulating the JOOSS sequence from chapter 11 in B:CP, programmed in Python.
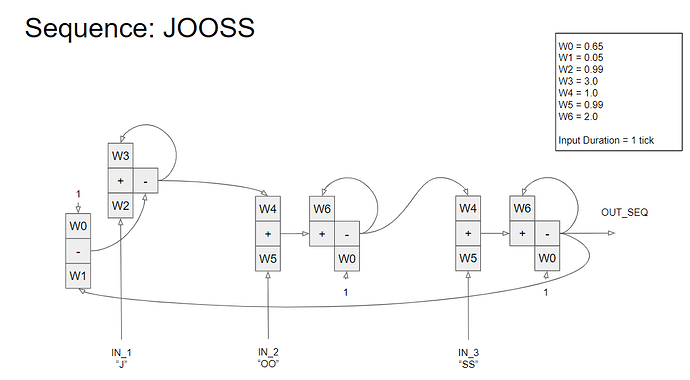
The goal is to not use programming language constructs but some element functional unit which can serve as basis for all PCT modelling (comparators, input/output functions, etc). See attached for the complete model.
I have attached an image of the model, with each of the 6 elements realized using the equation:
out(t) = s1*in1(t)w1 + s2in2(t)w2 + s3in3(t)*w3
where s is the sign (+ or -) and w is for a weight.
All signals are floats varying between 0.0 and 1.0.
Weights vary between 0.0 and 4.0.
So, the functional execution of the model is from left to right, sequentially, and the signals flowing from right to left is updated the next iteration.
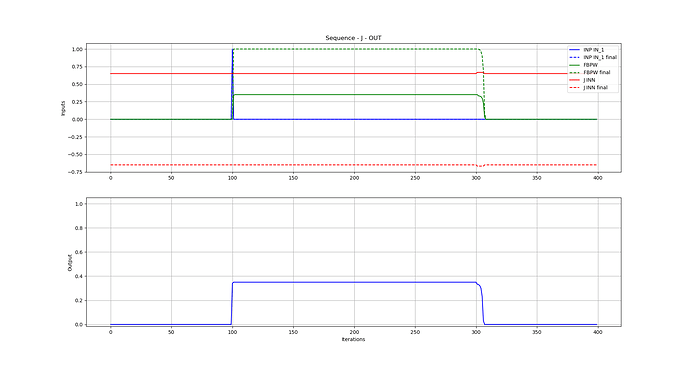
I have simulation plots as well, done with matplotlib (an example of the output of the second element is attached).
So, the model seems to work, following how it is described in the book.

My questions are:
(1) Has anyone else done a simulation of that sequence using functional elements (not lines of code) as building blocks? If so, which functional element worked for you? How did you simulate “time”?

(2) If able to implement the JOOSS sequence, has anyone actually tried to input a recording of someone saying the word “juice” and have if fed to this model and have the sequence be detected? I am aware this will not be simple, given that many sublayers in the hierarchy need to be added.

Paul

[bnhpct]

For starters, it should be OK to simulate the lower-level inputs and outputs. At any given level, the perceptual signals from the level below are the environment.

Yes, repurposing the same structure is one of Bill’s central insights, on the analogy of the diverse uses of functionally identical components in electronics circuitry.

What differentiates one comparator from another are its input functions (perceptual input and reference input) and output function (error signal). In other words, where it sits in the hierarchy:

1. What systems provide perceptual input, with what weights?
2. To what reference inputs does its error output contribute, with what weights?
3. What error output or outputs determine the amount of its configured (=remembered) perception it is to control as a reference value?
   Developments in machine learning have achieved astonishing results. But the developers have no idea what structures are being created in what they are pleased to call ‘neural nets’, and face recognition, for example, can be confused and confuted by hacks to which the human brain is not subject, and by wearing ‘adversarial’-patterned clothing one may become invisible to surveillance cameras.
   https://www.newyorker.com/magazine/2020/03/16/dressing-for-the-surveillance-age
   To that this AI may result in intelligence it is liable to be truly alien, i.e. different from human.

I suggest that a way forward is constrained machine learning, building a hierarchy of comparators, or at least a pair of adjacent layers with the lower levels simulated, and then constraining the random processes of reorganization to operating upon the interfaces between comparators.

[amatic]

Hello Paul, that looks pretty cool! Do you plan to share the code too?
For your 1) and 2), I haven’t seen anyone doing similar models for sequence perception.

In terms of functional elements, this might be a collection of input functions, I suppose.
How to model time in this case… Not sure. Often, time is modeled implicitly by not allowing big instantaneous changes in states of elements. That is, by making some of the elements have gradually changing states with a certain time constant, like leaky integrators.

[Paul]

Hi Adam

I have made the script available here:

jooss 0321.zip

I ran it with Python 3.7.2.

Regards

[amatic]

Here is my take on it: https://github.com/adam-matic/simcon/blob/master/sequences.ipynb
This is made with a python version (not extensively tested yet) of an analog computer simulator. Each group is made of 3 elements - a summator that sums all its inputs multiplied by weights; a generator that makes a short pulse simulating input event; and an amplifier simulating the thresholded neuron. The amplifier that is limited in value from 0 to 1, and the threshold is simulated by a constant inhibitory element.

[rsmarken]

It’s great that you guys are doing this! I haven’t been able to spend much time on trying to understand the simulation. But I assume what it does is put put an output of 1.0 as long as J OO S is happening. I’m not sure what would happen if the input were something like J EE S or J OO T. I presume the output would go to and stay at zero as soon as the input was not what it was supposed to be. Also I don’t know how this perceptual function deal with timing. What if the input was J OO S, with a long pause between J and OO. I think the output should go to 0.0 if the timing of the phonemes is wrong, even if the phonemes themselves are right.

But once you get this sequence perceiving system working what I think would really be great would be to then incorporate it into a control system that controls for producing the perception of J OO S. This would be a system that produces the sequence perception in the face of disturbances, which would be factors external to the control system that distort or interfere with the production of the desired phonemes.

I think this would be a very useful project because it would involve building a control system that controls a perceptual variable – in this case a variable sequence of phonemes – that is defined over time. I have not been able to figure out how to build a control system that controls such a variable. But it is the control of these kinds of variables – variables like what Powers calls sequences, events, (temporal) relationships, programs, principles and system concepts – that really distinguishes PCT from engineering and robotic applications of control theory which are oriented to controlling variables that are defined over instants.

[bnhpct]

@Paul

How did you simulate “time”?

Time is inherent in a sequence perception such as this, in which control of a prior perception initiates control of the next-succeeding perception.

In respect to the lower-level perceptions that are controlled in succession, the sequence controller may be said to retain a memory of what has been controlled and perhaps an anticipation of that which is yet to be controlled, while controlling whichever of them is ‘present’. But such words refer to perceptions as experiences rather than as neural signals, a distinction that we do not yet know how to unify.

Time is not only a function of sequence perceptions. More generally, time is perceptual means to separate one perception from another. Just as perceptions are separated in the three dimensions of space even as they are integrated in a single higher-level perception time is a perception at a level which receives perceptual input constructed from memory (past) and imagination (future) as well as from current environmental inputs. Sequences are among these.

[Paul]

Thanks Adam for the simcon repository link.
I have been studying it in detail and comparing with what I have done myself.
I have a doubt about the integrator block. i find the implementation a bit strange:
sum_of_inputs = sum([self.ins[i].state * self.ws[i] for i in range(N)])
self.next_state = self.state + (self.old_input + sum_of_inputs) * (self.dt / 2)
self.old_input = sum_of_inputs

Seems there are two integrators (two states, that is two variables maintained/saved and used in the next iteration) and a fixed leak element (dt/2) in the middle. Do you know if there is any particular reason for this? Any particular behaviour or function in mind with it?

As far as I understand it, while a net positive input is applied, first state will increase to maximum, then the second state to some maximum after a while (the delay due to the dt/2 term). I cannot see the maximum value, so the input should be deasserted as some point, after which the first state will decrease to 0 and then the second state.

From simcon.ipynb:
“The integrator requires an initial decimal value for its output. It
takes up to 99 inputs, each with an assigned weight. The “in1” etc.
entry is the symbolic name of the output from another block; the
weight “wt1” etc. is a decimal number. The sum of inputs is
automatically multiplied by “dt”, the basic computing interval,
before being summed into the output.”

And this integrator does not match the time integrator circuit shown in Fig3.7 in B:CP.

Paul

[amatic]

Simcon was originally a C program, by W. Zocher and Bill Powers, here is their source code as an additional reference: simcon5.2. It can be run in in DosBox. I’ve mostly copied their code and adapted it for python. Their documentatation does not always match the code, I think the code is a newer version.

The integrator block implements the trapezoidal rule for integration, so the result is more accurate than Euler integration, though not by much.

For Figure 3.7, you’re right, this integrator in simcon is a digital approximation of an analog integrator. Latest analog computers had electrical integrators, and before them there were mechanical integrators. The time integrator in B:CP is a hypothetical neural implementation of an integrator or neural signals, firing rates, I guess.

[Paul]

Hi Bruce
Actually I was referring to time at a lower level, at the execution level, the algorithm for updating the processing elements (PE) in a network/design.
I see that in simcon there are two options: by default all PE’s with a state will update their next_state from current inputs. Once all PEs have an updated next_state, this value is assigned to the state to serve as input to PE’s in the next iteration. This causes a form of parallel emulation: all PEs are updated in parallel.
Secondly, PEs can be grouped so that their state is immediately updated and so that that value can be used within this iteration by PEs that will execute after this PE. This forces the delay of a signal between such PEs to be 0, as opposed to deltaT (the iteration/network update period).

I have seen this parallel emulation in articles of Steels and other Behaviour-based AI people in 80’s and 90’s, and by Barbara Webb using real-world cricket chirp recordings with a simulated cricket brain.

I have also used this method myself, and it works okay, as long as you keep track of the delays through PE’s (a signal travelling through more PE’s will have longer delay). Also, one must not think that PE’s drawn far apart on a piece of paper during a functional design, means the signal between them takes longer to reach.
That is, if all PEs update each iteration, and each PE’s state can serve as input to any other PE, then it means the distance is the same between all PE’s, that is, each PE is equally far away from any other PE. So the distance a signal travel through the network is counted by the number of PEs it passes through, yet being always one iteration distance away from any other PE.

While writing software, once can deal (has to deal) with this strange spactime effect, and be even more careful in multicore software designs (I guess for cached designs as well, near versus far memory). So, software architectures define things like X ms tasks, to ensure at a higher level the timing is under control.

The problems specifically come in when simulating parallel networks on a larger scale. For example, Izhikevich commented that his simple spiking neuron model needs to use a manual (programmed) step in the code to reset the spike from its high peak to a reset level. (See: Hybrid spiking models, 2010) This can be avoided (that is, completely continuous implementation) but would require the deltaT to become very small, which requires more computation power, and thus is impractical.

So, to me the time-space issue is a real problem for large designs, and I don’t have the answer yet, although I have spent too many hours on it.

So, that was my motivation for specifically asking how time is dealt with in other designs.

Regards
Paul

[amatic]

Simulating parallel analog computations clicked for me with Calculus in Context, the first 3-4 chapters. For scaling up, I’m guessing, maybe software in electrical circuit simulation area, like SPICE or similar could give some pointers.

[bnhpct]

@rsmarken

Also I don’t know how this perceptual function deal with timing. What if the input was J OO S, with a long pause between J and OO. I think the output should go to 0.0 if the timing of the phonemes is wrong, even if the phonemes themselves are right.

Perhaps this requirement for temporal juxtaposition defines the difference between an event an a sequence. A sequence can be interrupted, often by another sequence as I showed in Manchester, and then resumed. An event like a word can be interrupted only briefly and fortuitously, e.g. by a hiccup, not by control of another event or sequence. Wordplay like “unbefuckinglievable” actually supports this generalization by its rarity and by other aspects that make it a special case.