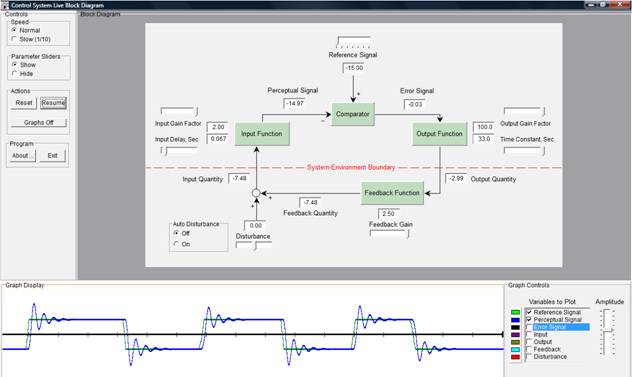
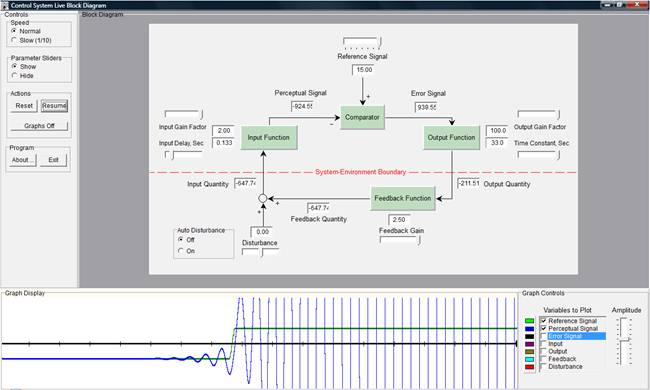
Well Rick, I think that your provocation was not necessary. But you can't
jump out of your skin.
I put my answer somewhere in the place of your provocation.
···
-----Original Message-----
From: Control Systems Group Network (CSGnet)
[mailto:CSGNET@LISTSERV.ILLINOIS.EDU] On Behalf Of Richard Marken
Sent: Sunday, December 22, 2013 9:12 PM
To: CSGNET@LISTSERV.ILLINOIS.EDU
Subject: Re: Stability and Control
[From Rick Marken (2013.12.22.1210)]
Bruce Abbott (2013.12.22.0935 EST)--
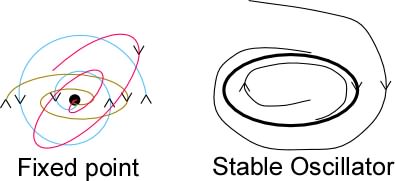
BA: W. Ross Ashby's definition of stability. According to Ashby, "Every
stable
system has the property that if displaced from a state of equilibrium and
released, the subsequent movement is so matched to the initial
displacement
that the system is brought back to the state of equilibrium" (Ashby,
1960).
Rick Marken has asserted that stability is a property that properly
belongs
only to equilibrium systems, to be distinguished from the property of
control, which belongs only to control systems.
RM: Not quite. I am saying that the "stability" described here by
Ashby -- the stability exhibited by what we can call "equilibrium
systems" -- is not the same as the stability exhibited by control
systems. In other words, I'm saying that the stability described by
Ashby is not control.
BA: Rick bases this assertion
on the definition of stability provided by control engineer Brian Douglas:
'Stability is a measure of a system's response to return to zero after
being
disturbed.' From this statement Rick concluded that stability refers only
to systems that return to their initial state (zero deviation from it)
following a impulse disturbance. Control systems, on the other hand, can
counteract even continuous disturbances. From this distinction, Rick
concluded that stable systems and control systems are different kinds of
system.
RM: Not correct. What Rick concluded is that the _behavior_ that
Douglas (and Ashby) calls "stability" -- the return of a variable to
the initial, equilibrium or zero state after a transient disturbance
-- is different than the behavior called "control" -- where a variable
remains in an initial, equilibrium or zero state, protected from the
effects of disturbance (sorry Boris).
HB :
Rick how can "variable" remain in "unchanged state" ? Even without a tiny
oscilation ?
And you call the mechanism, which "keep" variable in unchanged state" or
cause the variable to remain in the same equilibrium, initial, zero state -
control. Did I understand you right ?
I'm wondering how would you classify behavior of Watt's governer (Corlis
engine) or thermostat? By YOUR "definition" first is "protecting" the
controlled variable speed and the second is "protecting" the controlled
variable temperature, all the time "keeping" both variables in "unchanged
state" or as you say "remaining them in initial state" probably all the time
of control. How am I doing ?
Bill described the Watt's governer together with the engine as : "The
flyball governer, toghether with the engine it goverens, belongs to a large
class of devices known as negative feedback control system. These control
systems.//.can explain a fundamental aspect of how every living thing works,
from the tiniest amoeba to the being who is reading these words. The
mechanism by which this self-regulating machine worked was just about 100
years old". (B:CP, 2005). Notice that he is describing the mechanism as
self-regulative not "protecting".
Similar description of Watt's governer you find in Ashby's book. Only that
he is talking about stable system. ".if any transient disturbance slows or
accelerates the engine, the governer brings the speed back to the usual
value. By this return the system demonstrates it's stability. In both cases
"the field" or "aal line of behaviors" show changes in respect to initial
state. Or we could say that "lines of behaviors" starts and ends in the
initial position (zero state). They didn't mentione "remaining" variables in
initial state.
The same mechanism goes for Thermostat. You can find it in books of both
authors.
Oh, I don't know why I boder myself with citations and definitions. You just
got through the Bill's book (2005) and probably you know citations and
defitnitions "by heart" . :))
BA: But Ashby's definition of stability basically states a 'Test for the
Stable
System.' Equilibrium systems like Douglas' ball-in-a-bowl example meet
this
test: push the ball away from the bowl's center and release it, and the
ball
returns (after a few oscillations that gradually die out) to the bottom of
the bowl. By definition, the ball's position is stable. But good control
systems also meet this test: After an impulse disturbance, the controlled
variable returns to its initial value. So control systems that behave
this
way are stable systems.
RM: I have no problem saying that both equilibrium and control systems
are stable systems as long as it is understood that control and
stability are two different phenomena and , thus, require quite
different explanations. You are saying that stability is seen when a
variable returns to its initial value after an impulse disturbance.
You correctly note that by this test both an uncontrolled variable --
like the ball in the bowl -- and a controlled variable -- like the
distance between cursor and target -- appear to be stable. But if you
apply a continuous rather than a transient disturbance -- as in the
TCV -- you will quickly see that the ball in the bowl is _only_ stable
while the distance between cursor and target is controlled. This is
the important distinction (from a PCT perspective) because behavior
that is _only_ stable can be explained without the need for control
theory; behavior that IS control can be explained only by control
theory.
Psychologists who don't want to look at behavior as a control
phenomenon (because it would require them to see behavior as
purposeful) are, therefore, happy to see the behavior of living
systems as being like that of the behavior of systems that are _only_
stable -- like that of the ball in the bowl. That way they don't have
to confront the fact that the phenomenon they are trying to explain --
the behavior of living organisms-- is not just stable but also a
process of control. Bill was always having problems with people who
said that control theory is unnecessary because we can use
"equilibrium" theories -- ie. lineal causal theories -- to explain the
behavior -- when we tried to present PCT to conventional
psychologists. Indeed, in a talk I gave at Ucla a few years ago one of
the prominent professors in the audience scoffed when I said that
purposeful behavior is control and gave the example of the ball in the
bowl to show that all this control theory stuff was unnecessary; it's
all just the work of "equilibrium systems.
So while this discussion about the distinction between stability and
control may seem impossibly esoteric and trivial to many on CSGNet, it
is very relevant and real to me because I have experienced the effects
of treating stability as equivalent to control -- in the form of snide
reviewer comments on my articles and in haughty attempts at "gotcha"
remarks at conference presentations. I don't really mind it when it
comes from people who don't understand -- and clearly don't _want_ to
understand PCT -- but it saddens me when it comes from people who are
ostensibly fans of PCT.
BA: The distinction to be made is not between stable systems and control
systems, it is between equilibrium systems and control systems.
Equilibrium
systems (like the ball-in-a-bowl) are passively stable, returning to their
initial state after an impulse disturbance by converting the energy in the
disturbance to restorative force. When given a continuous disturbance,
they
simply move to a new equilibrium value rather than returning to their
initial value. Control systems are actively stable: they use their own
energy source to actively oppose the effect of a disturbance on the
controlled perception, whether the disturbance is brief of continuous.
RM: Right, two different mechanisms to explain two different
phenomena! If Douglas (and Ashby) had made that distinction clear I
would have had no problems with them.
Best
Rick
In the real world, equilibrium and control systems often work together.
For
example, many aircraft wings have dihedral - looking from the front of the
aircraft, they form a shallow V. A gust of wind acting from the side may
tip the aircraft's wing, but as soon as the gust is over, the wing will
level itself because the vertical component of the wing's lift is greater
for the more level half. But control systems aboard the aircraft (in the
form of a pilot or 'autopilot') add active control that can oppose even
continuously acting disturbances. Because of passive stability, the
control
systems aboard the aircraft do not have to work as hard to maintain good
control.
--
Richard S. Marken PhD
www.mindreadings.com
The only thing that will redeem mankind is cooperation.
-- Bertrand Russell
On Sun, Dec 22, 2013 at 6:35 AM, Bruce Abbott <bbabbott@frontier.com> wrote:
[From Bruce Abbott (2013.12.22.0935 EST)]
Boris Hartman posted something this morning that turned on a light for me:
W. Ross Ashby's definition of stability. According to Ashby, "Every
stable
system has the property that if displaced from a state of equilibrium and
released, the subsequent movement is so matched to the initial
displacement
that the system is brought back to the state of equilibrium" (Ashby,
1960).
Rick Marken has asserted that stability is a property that properly
belongs
only to equilibrium systems, to be distinguished from the property of
control, which belongs only to control systems. Rick bases this assertion
on the definition of stability provided by control engineer Brian Douglas:
'Stability is a measure of a system's response to return to zero after
being
disturbed.' From this statement Rick concluded that stability refers only
to systems that return to their initial state (zero deviation from it)
following a impulse disturbance. Control systems, on the other hand, can
counteract even continuous disturbances. From this distinction, Rick
concluded that stable systems and control systems are different kinds of
system.
But Ashby's definition of stability basically states a 'Test for the
Stable
System.' Equilibrium systems like Douglas' ball-in-a-bowl example meet
this
test: push the ball away from the bowl's center and release it, and the
ball
returns (after a few oscillations that gradually die out) to the bottom of
the bowl. By definition, the ball's position is stable. But good control
systems also meet this test: After an impulse disturbance, the controlled
variable returns to its initial value. So control systems that behave
this
way are stable systems.
The distinction to be made is not between stable systems and control
systems, it is between equilibrium systems and control systems.
Equilibrium
systems (like the ball-in-a-bowl) are passively stable, returning to their
initial state after an impulse disturbance by converting the energy in the
disturbance to restorative force. When given a continuous disturbance,
they
simply move to a new equilibrium value rather than returning to their
initial value. Control systems are actively stable: they use their own
energy source to actively oppose the effect of a disturbance on the
controlled perception, whether the disturbance is brief of continuous.
In the real world, equilibrium and control systems often work together.
For
example, many aircraft wings have dihedral - looking from the front of the
aircraft, they form a shallow V. A gust of wind acting from the side may
tip the aircraft's wing, but as soon as the gust is over, the wing will
level itself because the vertical component of the wing's lift is greater
for the more level half. But control systems aboard the aircraft (in the
form of a pilot or 'autopilot') add active control that can oppose even
continuously acting disturbances. Because of passive stability, the
control
systems aboard the aircraft do not have to work as hard to maintain good
control.
Bruce
--
Richard S. Marken PhD
www.mindreadings.com
The only thing that will redeem mankind is cooperation.
-- Bertrand Russell
-----
No virus found in this message.
Checked by AVG - www.avg.com
Version: 2014.0.4259 / Virus Database: 3658/6941 - Release Date: 12/22/13