[Martin Taylor 2009.01.22.12.59]
[From Bill Powers (2009.01.21.2218 MST)]
It seems to me that statistics (Bayesian or otherwise) is not relevant
to
the kinds of models PCTers have been working on, for the simple reason
that the models are expressed in terms of systems made of differential
equations, not propositional logic.
That’s really quite irrelevant. The models could be based on the I
Ching, for all that it matters.
The only reason I can see for using ideas like correlation and
probability in our modeling is to try to suggest, in a semi-meaningful
way, how accurately the control-system models represent behavior, when
we’re communicating with people who use statistics as their main means
of
evaluating theories.
That’s certainly one reason. I can think of others, much more relevant.
One, for example is “Which of these N control model structures more
probably represents what is going on in the person’s mind”. Another is
“Does the particular model fit the data so well because it does
represent what is going on in the subject’s mind, or because both the
model and the subject control well?”
It’s highly unlikely that real behavioral data
conform to the assumptions that underlie concepts like correlation or
probable error, such as having a distribution that is normal, Poisson,
or
something else with known properties.
True, and I did not use any of them in the demo analysis I did for Rick
(either last night or this morning). One can use them as a fallback
position, if one has nothing better to work with, but if you can avoid
using them, do.
Much simpler kinds of analysis are
sufficient to show when one control model predicts better than another
in
the realms we explore; if we had only ourselves to satisfy, why would
we
ever bother to calculate a correlation or a probability? You can see
that
the correlations are going to be almost perfect just by looking at the
data plots. The probability of such fits by chance is too close to zero
to measure.
“Probability of such fits by chance” is the language of significance
tests.
I should ask “correlations of what with what”? Anyone, whether they
understand PCT or not, would expect that when a person controls well,
their track will look like the inverse of the disturbance, and if a
model controls well, its track will look like the inverse of the
disturbance. Those correlations will be high, and necessarily the
correlation between model and person must also be high. It’s redundant
to show that it’s true in any specific case. Of course, if the model
track matches the person’s track when neither control very well, that
does tell you that the model may well mimic what the person is doing.
One can do a bit better, perhaps, by comparing three correlations:
person-disturbance, person-model, and model-disturbance. If the
person-model correlation is appreciably better than the other two, then
you would have a reason to argue that the model structure fits the
person’s machinery “better than chance”. This comparison can be done
whether the person and model control well or poorly.
If a difference can be reduced by
changing a single parameter, we’re looking at systematic effects, not
random effects. Even by eye one can see that the residuals are not
distributed unsystematically.
I’m, afraid my eye does not see that in the track you displayed, other
than possibly that the error seems to increase when the second
derivative of the track has a large absolute value.
On the other hand, if you mean you can modify P(D|H) by varying the
model parameters, that’s the point of optimizing, isn’t it? I did a
discrete version of that with the lag in Rick’s demo [ [Martin Taylor
2009.01.21.17.45 and Martin Taylor 2009.01.22.10.03]. But what has it
to do with random variation or the systematic distribution of residuals
(which I used in judging that it might be useful to try varying the lag
in Rick’s demo)?
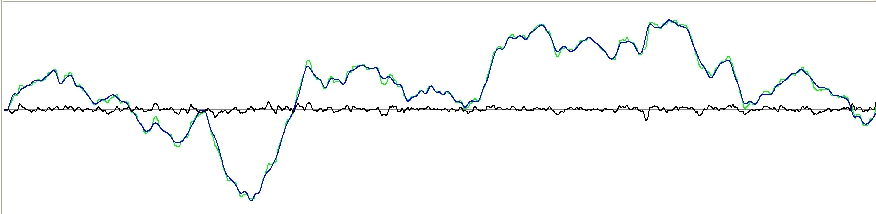
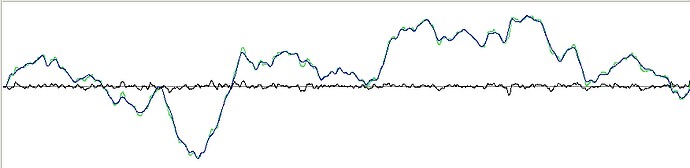
Here is the
fit of model mouse position to real mouse position over a one minute
run
(done just now) with medium difficulty factor:
The darker trace is the model prediction; the light green trace is the
real mouse position. I would guess that p is much less than 1E-10. The
RMS error is a little over one per cent of the total range.
“Significance Test” language again! “p” of what? Probability that the
subject is not controlling? Not a very interesting finding. Probability
that the model is a precise mimic of what the subject’s mind and body
is doing? I don’t think so. So “p” of what?
It really depends on what question you want to ask. The Ward Edwards
paper that really put me solidly on the Bayesian trail so long ago made
the point that the only really reliable test was the “InterOcular
Traumatic” test. In other words, he made the point that you started
with: that a good result needs no statistics. If you want your trace as
an argument that the person is controlling, and that the model is
controlling, the trace satisfies the IOT.
The situation, if the point is to show that both model and person are
controlling, is rather similar to a situation I once found myself in
with a paper I submitted to journal. I had six male and six female
subjects. All the males scored in the region of 5% on a task, all the
females scored in the region of 95%. I made the claim that there seemed
to be a sex difference. The editor wanted me to perform a significance
test, and I refused on the grounds not only that significance tests can
be used to prove ANY relation to be significant if you get enough data,
but more importantly, that the results satisfied the IOT. He controlled
the journal, and I didn’t publish.
Back to your trace. Do you also have the residuals between the model
and the (inverse) disturbance, and between the person and the
disturbance? When you plot the three together, how do they correlate?
Is there in fact any relation between their mutual relations and the
second derivative of the disturbance trace, as a by-eye check of your
trace suggests there might be, or is that apparent relation just a
visual illusion? If you make a 3D scatter plot of the sample-by-sample
values of the three residuals, does it look uniform (i.e. elliptical
with the main diameters parallel to the axes) or does it have a more
interesting shape?
The black
trace shows the actual residual difference between the two mouse
traces.
It is nothing like normally distributed.
Obviously. But that’s really not an issue, as I explained in connection
with Rick’s example. In fact, the deviations from normality are often a
cue to further enquiry as to what is going on. When and why do they
occur? It’s an aspect of the advancement of science.
Obviously, the uses for advanced statistical treatments of this kind of
data are minimal.
Obviously, I disagree.
As long as we continue to do the right kinds of
experiments, that will continue to be the case – and why do any other
kind? It’s not as though we have explained such a large proportion of
known phenomena that we have to start searching with a magnifying glass
for something to study. See my Essay on the Obvious.
Well, I’ll just ask a question about the trace you presented. Are those
apparent “blips” in regions of high values for the second derivative of
the trace reliable? Is it a trick of the eye that they are easily seen
in those places, or do similar excursions happen equally probably in
places with any value of the second derivative? If it’s not a trick of
the eye, what might that tell you about possible improvements in the
model?
Some things that seem Obvious are not necessarily what they seem.
Martin