Hello everyone! First time poster here.
I’ve been searching for PCT-oriented propositional logic empirical studies.
I found this thread at the CSGnet Archive, where Bill argued propositional logic operates at the 9th level of organization (program level). That discussion reminds me passages about logic and reasoning at Philip Runkel’s book (chapter 25).
That’s exactly the kind of modeling I’m looking for. Does anybody know studies in this area?
Regards,
Hugo
It sounds like you are looking for PCT models of how people reason, correlated with the kinds of language-like expressions that logicians write as representations of people’s reasoning.
To the best of my knowledge, the answer is no. So the field is open for you to investigate. But be sure to get a solid grasp of PCT modeling at lower levels first.
Bill recommended Miller, Galanter, & Pribram (1960) Plans and the structure of behavior as a collection of examples of what he thought of as program control.
Hi Bruce,
Thanks for the tip. MG&P is truly a classic worth re-reading.
I’m curious about which level of the hierarchy would you recommend to start this modeling process.
Most cognitivist approaches to programming abstract away sensorimotor details and start their models at parsing, rule following, conditional branching, etc. I don’t think that is enough (that’s why PCT attracted me), but I guess a general simplified architecture for the lower levels would be enough to build a first approximation of the higher levels of the model.
Regards,
Hugo
BTW, I think of it as planning rather than programs, a sticking place being the question how neural structures might maintain uninstantiated variables
“Plans are worthless, but planning is everything.” —Dwight D. Eisenhower
You’re on the right track. The underlying assumption in Cognitive™ psych and in Generative™ linguistics is that the brain creates an abstract symbolic representation of the world, melds sensory input into this ‘map’, computes plans for actions within the ‘map’, and issues commands through motor systems. Notions of feedback are limited to updating the map and fixing the plans.
Bill was unfortunately hampered by prevalent notions about language and consequently thought there must be abstract symbols beginning with his postulated Category level. As he himself said this should all be open to question.
Rules governing the parsing of strings of abstract symbols are something that cognitive psych avidly adopted from Chomskyan linguistics even as the Chomskyites got legitimation from CogPsych, two vines twining up on each other, their tensegrity however vacuous supporting thousands of careers as money flooded in for the old promise of the behaviorists, “prediction and control of behavior”, and for “command and control” in the military (“Computah! What is the disposition of enemy troops in quadrant four!”). Neuroscientists have a growing sense of being stuck in a specious cosmology and are trying to wrestle free of a tarbaby they can’t yet quite see as something separable.
I have advocated starting at the Sequence level observationally. When we have a good grasp of how to model sequence control within a hierarchical context, and how a sequence can be interrupted by another sequence and then resume, only then will will we have a basis for talking about conditional branching. How is the input function for initiating a sequence different from a condition for taking a branch?
I found it illuminating to observe my own planning process as I was working out how to repair an outdoor shower. That experience, and the attempt to document it, is why I think of the level above sequence control as the Planning level rather than a Program level.
the computational metaphor has been most beguiling, but the brain is not a digital computer.
Hi Hugo!
If you could give an example of a non-PCT-oriented empirical study of propositional logic then I might be able to tell you how a PCT-oriented researcher might approach the same study.
To the extent that actually doing propositional logic (rather than just doing in your head) is carrying out a program – and I suppose it is – then what Bill was saying is that doing propositional logical is a matter of controlling a program-type perceptual variable. According to Bill’s model a program-type perceptual variable is a variable controlled at the 9th level of the hypothetical control hierarchy.
I have done some relatively informal PCT-oriented studies of propositional logic in the form of tests to see whether control of a program-type perceptual variable is at a higher level in the control hierarchy than control of other types of perceptual variables, in particular, sequence-type perceptual variables.
The relative level of control of a perceptual variable is determined by what is essentially a reaction time test. An example of a study of program control can be found here. You can do this study yourself, though it will probably take a bit of practice before you are able to control the program even at the slowest display rate (allowing the longest reaction time).
This study could definitely be improved since there is a confounding variable – the program is defined by changes in two attributes of each object (shape and color) while the sequence is defined by changes in only one attribute of the objects (size). This should be fixed and maybe this is the kind of study you could do as a PCT-informed study of propositional logic. But even in its current form, this little study strongly suggests that controlling a sequence perception is a lot easier than controlling a program perception; a sequence can be controlled when it is presented at a much faster rate than a program. I’m sure that if the confound were eliminated this large difference would still be seen.
Bill’s model predicts that lower level perceptual variables can be controlled at a faster rate than higher level variables, if for no other reason than that neural control loops for lower level variables are shorter than those for higher level variables. Since my little study suggests that a sequence perception can be controlled at a faster rate than a program perception, it supports a prediction of Bill’s model, which is that program-type perceptions are controlled at a higher level than sequence-type perceptions.
The study also shows what it means to say that a program is a perceptual variable. In this study the program is a variable (with two possible states – two different possible programs) that is controlled by non-programmatic output; you just press or don’t press the space bar in order to keep perceiving the desired program. This makes it clear, I believe, that in Bill’s model what is controlled is input, not output.
That is one heck of an excellent book on Bill’s model. Phil’s book, as well as other books that will give you a good idea of what Bill’s model is about, are listed here.
Best regards, Rick
Planning is just controlling in imagination. We can control programs in imagination (like a game or battle plan) but we are also controlling many other types of perception in imagination when we do this. As Bill said (in the CSGNet thread that Hugo cited): “We can think (and act) at 10 other levels [besides programs] as well.”
Which is why living organisms are control systems rather than automata.
RSM
“Program level” is a metaphor, an informal supposition that certain neural circuits in the brain are functionally analogous to functions in computer programs.
Computer programming depends upon libraries and sub-libraries of functions, idioms, routines, algorithms. Broadly speaking, these are general patterns for solving specific problems. Programming organizes them into systems that make use of those patterns to solve specific problems or otherwise produce desired outputs given certain inputs. Maybe there are abstract general-purpose sequence-control loop systems that are employed by a variety of higher-level systems to control their diverse input requirements. Maybe there are abstract organizations of these into something corresponding to libraries and sub-libraries of functions, idioms, routines, and algorithms. As a general rule, computer programs, algorithms, routines, idioms, and functions as found in the computer science world do not implement negative-feedback control loops. In HPCT I should think every such function would be a control loop, but maybe someone has good reasons for the postulated Program level to be like program libraries in a computer.
There are other reasons that it is extremely difficult to make a direct analogy from posited neural structures to program structures. The appearance of these structures differs so much from one programming language to another. The ‘program language wars’ have long been a contested effort in defending ‘the devil you know’. This amusing talk by Andreas Stefik on actually applying scientific methodology to the learnability and human efficiency of computer programming languages (in the form of human factors research and usability testing) lays bare how and why computer programming languages are demonstrably counter-intuitive. “Counter-intuitive” seems to identify aspects in which they do not accord with how we think (a proposition complicated by the tangled and often denied relation of computer languages and of mathematical logic systems in general to language). A deep dive into Structure and interpretation of computer programs (SICP) can clarify the differences. It’s expressed in terms of one ‘religion’ (Lisp/Scheme). (Also here under creative commons.) A Javascript edition was published this year (2022). I haven’t done anything with that since I left BBN in 1994 and it’s not in my direction of work now, so I can’t be much particular help other than to set the signpost.
Some discussion of Rick’s demo is here and here.
/B
No, program perceptions are not metaphors. Bill was describing a type of perception – the perception of network of contingencies between states of lower level variables (X, Y, Z, etc.); contingencies such as "if X then Y else Z.
The fact that programs are perceptions is demonstrated by one’s ability to control for the occurrence of a particular program in my program control demo.
Programs were being carried out by people well before computers were invented. Indeed, the machines that carry out programs were invented to imitate the behavior of people called “computers” who were carrying out a program of computations. Indeed, that’s why we call those machines (whether analog or digital) “computers”.
Again, the programs controlled at the “program level” in Bill’s model of behavior are perceptions, not metaphors. The program level of the hierarchy of control consists of control systems that control programs; and control systems control perceptions, not outputs or metaphors. So Bill was quite clear that the program level of control controls program perceptions.
RSM
Yes. The point is, controlling in imagination at what level toward a goal mandated from what level above. Then, having worked out what is required, in ordinary human affairs the execution rarely has the automatism of running a computer program. Unforeseen disturbances in an unpredictable environment require further trial and error improvisation. The benefit of planning is to have a ‘place’ to get back to after such interruption, to get ‘back on track’ toward the goal.
“The unexamined life is not worth theorizing about.”
I agree: that to which the expressions “Program level” and “Program perception” refer (what you’re talking about here) is not a metaphor, it is a matter of investigation. However, the reason I put the words “Program level” in quotation marks is because the expression “Program level” is a metaphor. The metaphor presupposes that the control processes in question correspond to expressions in applied mathematical logic a.k.a. programming languages. I doubt that presupposition. Some of my reasons for doubt are nearby in this topic. Note also that the human-readable code is transformed into machine code instructions which cause computer state changes, and that those instructions are grotesquely disanalogous to anything going on in the brain. A discussion of logic gates is posted here.
Ignoring the metaphorical character of the labels “program level” and “program perception” risks covertly inviting the metaphor to prejudice the investigation. Presuppositions are often sneaky, but this presupposition is quite explicitly baked into your demo, not sneaky at all.
Every perceptual input function can be represented by an *if … then … * expression (if {inputs} then perception). Facile translation into program-logic language obviously is inappropriate for PCT in this case. Abstraction makes it difficult to make the same kind of assessment about the presupposition that ‘Program control’ can be represented by the logico-mathematical structures of a programming language.
So how about you identify an example of program control in your own personal experience and model it. That means start with the phenomena instead of starting with the theoretical constructs provided by a computer program. Phenomena first.
In Bill’s model the phrase “program level” refers to control systems that control program-type perceptions. There is no presupposition that the control processes involved in the control of these perceptions are any different that those involved in controlling a cursor on a computer screen, the area of a rectangle or the distance between a fielder and a fly ball. There is certainly no presupposition that the control processes involved in the control of program-type perceptions “…correspond to expressions in applied mathematical logic a.k.a. programming languages”. In Bill’s model, programs are objects of control, not the means of control.
No, they are not.
The consequences of the operation of perceptual input functions can be represented by if…then expressions, though not very economically. The function itself can’t.
The phenomenon has already come phirst. It is the observed control of the program in my program control demo. I haven’t been able to model this control because I don’t know how to build a program perceiving perceptual function – a perceptual function that produces different outputs depending on which program is running. I was kind of hoping that Hugo might be able to help me on that.
RSM
Hi Richard!
I have the classics of the 1980s in mind, such as P. N. Johnson-Laird studies on syllogisms, production systems (Newell, Klahr, Anderson), and older Piaget-like experiments with children as well.
I totally agree. Building interpreters for programming languages helped me a lot to understand how control flows during program executions. For instance, recursion is not that hard for us, but it is far from trivial to implement it efficiently in interpreters without dealing with program interruption, branching, resuming, stacks, etc.
I’m also interested in explaining how procedures (cognitivist sub-programs) become “heuristics”, but in PCT terms. There are studies under the Piagetian umbrella (i.e. Madelon Saada-Robert, Alex Blanchet) which postulated that procedures are perceived by the subject as functionally relevant to present situation, while not restricted to it. Cognitive functioning would start by trial and error (routines independent of the goal), gradually organized into primitives (key parts of the problem identified), then finally merged into (purposeful) heuristic procedures. So far so good, but those models ignore search space size and other tractability issues. Which mechanisms “search”, “select”, and “activate” the appropriate procedure in a given situation? Are they psychologically and neurologically plausible? I guess the PCT framework could offer a better explanation through input functions and reference values between levels.
Thank you for the careful recommendations. It’s a nice coincidence, because I’ve ordered “Mind Readings” last week. I’ll check the example study you pointed to.
Kind regards,
Hugo
I hope I didn’t misunderstand your goals, Richard. Your statement seems to describe, using precise PCT constructs, what I’m trying to build. I cited the routine-primitive-procedure model above as an example of the changes in behavior I’m investigating. That Piagetian model lacks a control hierarchy with levels accounting for different outputs “depending on which program is running”.
My aim while asking recommendations of experimental propositional logic studies was to find how PCT researchers formulate operational definitions of a simple program, how they observe it controlling perceptions from lower levels, and sending perceptual signals to higher orders. I understood the TCV method for basic motor controls, so I have to study your program control demo to get how did you apply the same approach to the program control level.
This is a very rich discussion to follow. Thank you Richard and Bruce!
Your demo assumes that the person interacting with the demo is doing this by ‘running’ the same program logic that the computer code specifies for the computer.
On that hypothesis, just have a copy of the same program running and a function that compares the outputs of the two.
Unfortunately, there is no hierarchical control in that approach, and so no difference in performance corresponding to sequence control vs. program control. It skips the Sequence level entirely.
Hi Hugo
It would be nice if you could pick from the works of these authors one experiment on propositional logic that has produced some clear, quantitative results and is one that you think is “classic”. It would be an interesting challenge to see how Powers’ control theory model would explain the results of such an experiment.
Best, Rick
Hi again Hugo
I’m not really interested in other people’s models because other people don’t understand behavior as a control process. I’m just interested in seeing how one might go about building a control model that can account for the behavior seen in my program control demo, where a person can be seen to be controlling for the occurrence of a particular program of events. It can’t be a program of outputs that control the program because the state of the program can only be affected by pushing or not pushing the space bar. So the outputs (press/no press) that control the program are not, themselves, programmatic.
In order to keep the desired program happening in the demo ( the desired program – the one you are asked to have keep happening – is “if the shape is circle, the next color is blue; else, the next color is red”) the control system has to be able to perceive what program is running. It’s the development of that perceptual function – one that perceives which program is happening – that I need help with.
According to Powers’ model of behavior, producing a program of activities is a matter of producing a perception of what program is happening, whether that program is being produced by the actions of a computer (as in the demo) or the actions of a person (as when you cook from a recipe). If we could build a model that controls a program-type perception it would go a long way to helping people (who are willing) understand what Powers meant by control of programs.
There are not many researchers formulating such operational definitions. In my demo (and I think in Powers’ description of his mode in B:CP) program level perceptions are operationally defined as a “network of contingencies”; that is a network of if-then choice points.
Higher level control systems don’t control perceptions from lower levels. But there has been little or no experimental work done on hierarchical control. Powers model is completely different from existing models of how organisms do propositional logic, etc. so it’s one step at a time and not many people are interested in taking that first step.
My program control demo is exactly analogous to the basic motor control task, except that the controlled variable is a program (or sequence) rather than the position of a cursor. There are two possible programs that are happening in the demo so the controlled variable has two possible values. The person doing the demo tries to control the program by acting to keep one of those programs happing, much like keeping the cursor on target in the motor control tracking task.
Best, Rick
No, it doesn’t. All it assumes is that the participant is able-- or can learn to be able – to control the perception of a program of events happening on the screen.
There was definitely hierarchical control on the perceptual side as evidenced by the much slower rate of presentation required to be able to control the program compared to the sequence. I think you can get an idea of what was going on by looking at the experiment described in this paper. See in particular Fig 2.
And you don’t know that the sequence level was skipped. But whether it was or not is irrelevant. The fact that a much slower presentation rate is required to control a program compared to a sequence is strong evidence that programs are perceived and controlled at a higher level of the NS than sequences.
RSM
Your program code says “if the shape is circle, the next color is blue; else, the next color is red”.
The subject can tell when the program is running and when it is not by controlling two sequence perceptions in parallel:
Your demo can’t tell whether I’m doing that or controlling a contingency as specified by your pseudocode (and your computer code). Nor could you tell which I am doing, if you were observing me, except to believe my testimony. I reported all this in February 2018 (links earlier in this topic).
Each sequence requires control at the configuration level followed immediately by control at the sensation level. I found that integrating these different levels into a sequence perception, and maintaining control of the two disparate sequences concurrently, resulted in hesitations and errors. This is probably related to how sensations are perceptual inputs to configurations. It accounts for the difference in speed of performance.
Reciting the pseudocode to determine whether or not to press the spacebar was far slower. It may be that long practice would create a perceptual input function that would enable efficient control. But how reorganization resolved the problem in neural structures would still be unknown. Reorganization might very well resolve it as concurrent control of two sequence perceptions. We have no way of knowing by means presently available to us.
What is of interest to me, and I believe what is the reason for Hugo’s inquiries about propositional logic, is not a perception whether or not a computer program is running (which is control by a system above the Program level), but rather how a living control system does what we may perceive as controlling at the Program level. This is what the phrase ‘program control’ means to me.
‘Program control’ in your sense of the term is done by a higher-level system recognizing when a program has stopped and acting to restart it. This is very different from program control at a Program level of choice points and contingencies. (If the analogy to computer programs and mathematical logic is at all serious, much more than choice points and contingencies is involved.)
Often, we do not know what the output of a program should look like. That’s why we have programs, to produce solutions to problems that are not known in advance. Even when we do know what the desired output looks like, evaluation of output is a separate step. Even when a recipe is a network of contingencies (many if not most are sequences without choice points; the selection of alternative ingredients is done before starting) the perception of when it is completed and the perception of whether or not it has delivered the desired results are entirely distinct. Yes, the cook moves immediately to taste the broth, and may then make adjustments (usually straightforward perceptual control, “needs more salt”), but the last step of the recipe has been completed.
All that a system that ‘calls’ a program knows is whether or not the program has delivered its output. Verifying that the output is correct, and behind that verifying that the program is correct, is a different problem. Your demo proposes that the system that does ‘program control’ in your sense of the term (i.e. recognizing when a program has stopped and acting to restart it) knows what the output should look like. That scenario might happen in nature, but I’m not immediately aware of an example. Maybe you are?
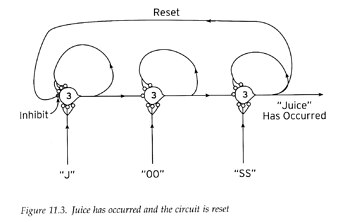
I think it’s much more likely that the program structure sustains an ‘in progress’ signal back to the calling system, and stops doing so when the program has completed. I think this is probably how sequence control works. Bill’s diagram for recognizing sequences issues a ‘reset’ signal on completion, which goes back and stops the millworks.
A program is a particular arrangement and interconnection of sequences and sub-sequences. If the perceptual state resulting from a sequence is connected to the input functions of two alternative sequences together with a ‘continue’ signal from a calling system at a higher level, that is a choice point which is decided by the match of that perceptual state to one input function or the other.
Excellent. That is your theory of how a program is perceived. And I think it is on the right track.
The participant has no control over the contingencies in the demo; the participant only has control over whether certain contingencies are occurring.
The sequences that make up the target program – circle->blue, square ->red – cannot be controlled in this demo. All that can be controlled in this demo is 1) whether the program “if circle then blue else red” is occurring or 2) whether the sequence “small medium large” is occurring.
Well, it’s not what it means in Bill’s model of behavior. In that model, it is hypothesized that program perceptions are controlled by control systems at the program level – systems that have perceptual functions that can perceive whether or not a particular program is occurring. Control systems above the program level are hypothesized to control perceptions of principles – perceptions that can be controlled by varying the programs controlled by the lower level program control systems.
Maybe in your model that’s true. But that is not true of Bill Powers’ control model, which is the one I’ve always preferred;-)
I think we generally know what the output of a program (however implemented) should look like; we just don’t know what it actually will look like. I know, for example, what the result of carrying out the program of activities specified in a recipe for brownies should look like, it just doesn’t always look that way.
The demo doesn’t “propose” anything; it shows that a person can control (and, therefore, must be able to perceive) the occurrence of a specific program of events (if circle then blue else red). The programs of events that are perceived happen to be produced by a computer program. But you would get the same results if the program were produced by some other means (the only other one that comes to mind is having a person hold up 3x5 cards with red and blue shapes held up in such a way that the sequence of cards implements the programs (if circle then blue else red) and (if circle then red else blue).
Again, this could be taken as a proposal for how to build a perceptual function that puts out differential signals depending on which program is running. It would be great if you and/or Hugo could create a working prototype of such a perceptual function.
RSM
