···
Martin Taylor (2016.12.19.11.58)–
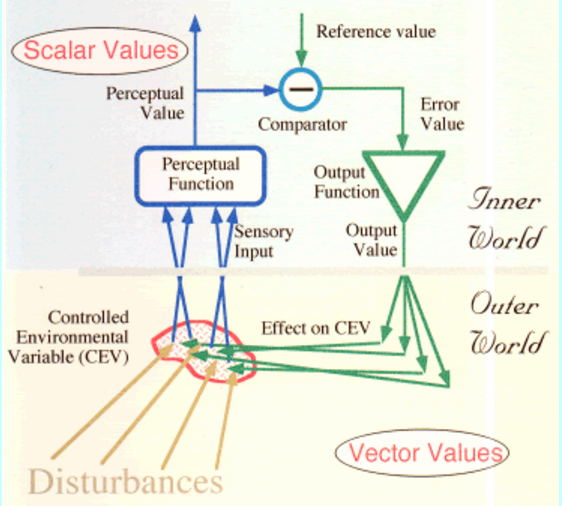
MT: Compare the Figure in
http://www.mmtaylor.net/PCT/Mutuality/control.html
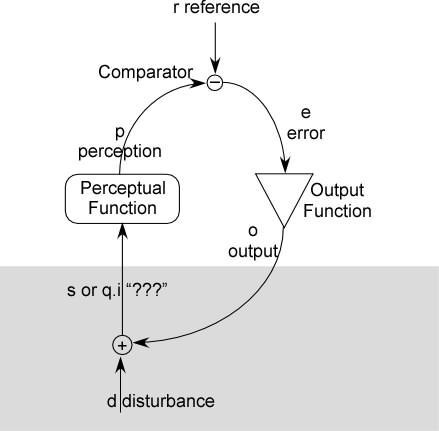
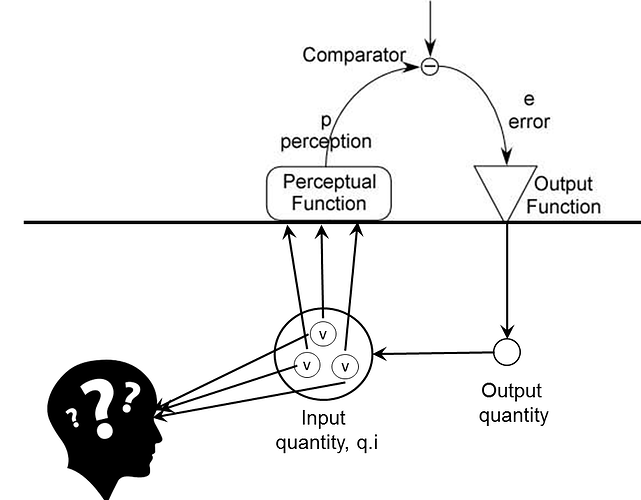
RM: I’ve taken the liberty of copying it so people could see them next to each other. This is, indeed, an excellent graph, equivalent to mine in all respects except for my inclusion of an observer of the controlled variable (or controlled quantity).
MT: and note that if the perception is a scalar value, the CEV itself MUST
mathematically be a scalar quantity,
RM: This is true if CEV is a synonym for controlled quantity. Since, as demonstrated in my version of the diagram, the controlled quantity is a perceptual variable in the observer that corresponds to the perceptual variable controlled by the controller, then the CEV is, indeed, a scalar perceptual variable in the observer. However, this controlled quantity is a function of many sensory or perceptual input variables. So the controlled quantity, which exists as a scalar variable in the observer and controller, is defined by a function that converts variations in the these sensory or perceptual variables into variations in these scalar perceptual variables.
RM: There are many scalar perceptual signals in the nervous system and they are all the same: variations in the rate of neural firing, according to PCT. So if all perceptual signals are the same, what accounts for all the different perceptions we have? Why is the perception of the color of a rose different than the perception of the principle of honesty, for example? According to PCT redness and honesty are both variations in neural firing rates; scalar variables. The difference, according to PCT, is in the functions that transform sensory or perceptual inputs into these scalar perceptual signal outputs. The perceptual signal that corresponds to the color of a rose is presumably produced by a perceptual function that converts sensory inputs corresponding to the amplitude of different wavelengths of light into variations in a scalar perceptual output variable that correspond to variations in the redness that we perceive; the perceptual signal that corresponds to the principle of honesty is presumably produced by a perceptual function that converts perceptual inputs corresponding to, say, relationship variables into variations in a scalar perceptual output variable that correspond to the variations in honesty that we perceive.
RM: I find it helpful to look at the PCT model of perception in terms of the Hubel/Wiesel receptive field studies, where they found that the rate of firing of single cells at different points in the afferent optical pathway varies in proportion to variations in certain characteristics of the sensory input. The concept of a receptive field is very much like that of a perceptual function: it takes the sensory array as input and produces variations in a scalar variable, neural firing rate, that vary in proportion to variations in relevant aspects of the sensory array. For example, the firing rate of some neurons in the visual cortex varies in proportion to the degree to which a line in the sensory array is oriented vertically; when the line is horizontal the firing rate of the neuron is near zero; as it moves to approach vertical firing rate increases to maximum.
RM: Although a difference in perceptual functions can account for the difference in the aspects of the sensory array that are represented by variations in neural firing rate in different cells, the fact is that the firing rate in all neurons is the same. So there is still the question of why we experience these different perceptions as we do. Why is red experienced as red and honesty as honesty? Why does the world look the way it does, instead of the way it is: different rates of firing in different neurons? This is an interesting question because our models are able to control perceptions that are represented as neural firing rates. Our models don’t experience the perceptions they control in the same way as we experience those same perceptions. My model of control of area, for example, controls a scalar variable, p, that happens to be the output of a perceptual function that computes height*width; it just keeps that p number equal to that reference number. It doesn’t experience area as I do when I control area; the model experiences only a number; yet it controls area exactly the way I do. If control is possible without the extra added attraction of the controlled perceptions “looking” a particular way, then why do those perceptions look a particular way.
RM: I think this is called the “hard problem” of consciousness: Why are neural impulses experienced as they are? It seems to me that there are harder problems of consciousness – like “What is it?” and “Why is it there?” – and this so-called “hard problem” may not even be a consciousness problem. Indeed, it may not even be that hard; my answer to it is simply that that’s the way the world looks when you are a collection of neurons. But now that I think of it (and I’ve actually never thought of it before) I think the interesting question for PCT theorists is “Why do we see the world as we do when PCT modeling (and robotics, for that matter) shows that it is possible to successfully control things like the position of a cursor, your position relative to a fly ball, etc, when the variables under control – cursor position, ball position, etc – are represented only as scalar variables – that is, as numbers?”
Best
Rick
a point on some curve in the
high-dimensional space determined by the properties of the space and
the perceptual function. The reference value for the perception is a
scalar and the perception itself is a scalar, so no variations in
the real world (whatever it might be) can influence anything but
that scalar value.
For more explanation than I can offer in a quick e-mail, read
carefully Part 2 of
http://www.mmtaylor.net/PCT/Mutuality/index.html . (You can
read more of it if you want, if you are happy with vector
representations and discussions of side-effect interactions in the
development of social structures. It also includes a discussion of
reorganization that Bill P praised.).
Also, you will find a quite different way of looking at the whole
loop in a message I hope to post very shortly.
Martin
–
Richard S. Marken
“The childhood of the human race is far from over. We
have a long way to go before most people will understand that what they do for
others is just as important to their well-being as what they do for
themselves.” – William T. Powers
RM: Here's a slight revision of your diagram based on
Figure 1 in Powers (1973) Feedback: Beyond Behaviorism, Science ,
179, 351-356, reprinted in LCS I (figure is on p. 66).