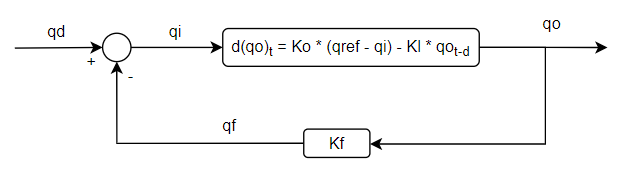
Say we have a standard tracking task, and a standard model, with the usual variables and functions.
For a disturbance as a sum of sines, Ko = 20, Kf = 2, and Kl = 0.01, we get this time plot:
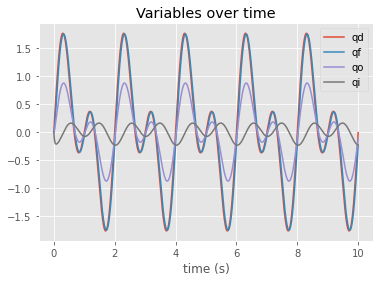
We can see the input variable qi relatively stable.
In psychology, the stimulus and response definitions are arbitrary. If we define the stimulus as the proximate stimulus, qi, and the response as the change in behavior, or d(qo), the derivative, then we can approximate the organism function by plotting those two variables.

Changing Ko to 120
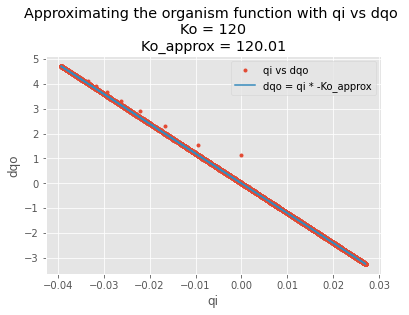
Adding noise to the disturbance makes the estimate of Ko lower, but still in the ballpark.

The disturbance-output function still approximates the inverse of the feedback path.

So… pretty convenient. If we use the TCV to find the correct definitions of the stimulus and response variables, we can also try approximating the organism function like this. After all, the organism is just an input-output system, and only when it is interacting with the environment, the loop becomes closed.
The trick is in using the correct measures. We need to assume the organism function is an amplifier (a leaky integrator) with a gain Ko. We also need to assume that the reference level qref is zero.
Haven’t used this method yet with any real data, but it just makes me think. Maybe some SR laws found in psychological literature do reveal something about the organism.