[Rupert Young (2014.04.22 18.00)]
The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
Regards,
Rupert
[From Rick Marken(2014.04.22.1910)]
I sent this to Rupert instead of CSGNet, which I realized when there were no comments on it. So here’s the forwarded version:
[From Rick Marken (2014.04.22.1450)]
Rupert Young (2014.04.22 18.00)
RY: The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
RM: This is a great question, Rupert! I would like to hear how some others would answer it before answering it myself. So I’ll wait a bit and see if anyone else replies. I would really like to see what others think is “wrong” with this picture (if anything) from a PCT perspective.
Best
Rick
Richard S. Marken PhD
www.mindreadings.com
It is difficult to get a man to understand something, when his salary depends upon his not understanding it. – Upton Sinclair
–
[From Fred Nickols (2014.04.23.0731 EDT)]
I looked at the diagram and the drawing and read portions of the paper. I’m not sure I can put my finger on anything wrong. If I substitute thermostat for governor and furnace for steam engine then it seems to me that the comparator is outside the thermostat/governor and I’m not sure that’s right. The thermostat turns on and off the furnace and the governor increases or decreases steam to the engine. But, I suspect Rupert sees something wrong, as do you, Rick, so I’m happy to be enlightened.
Fred Nickols
From: Richard Marken [mailto:rsmarken@gmail.com]
Sent: Tuesday, April 22, 2014 10:09 PM
To: csgnet@lists.illinois.edu
Subject: Fwd: What’s wrong with this picture?
[From Rick Marken(2014.04.22.1910)]
I sent this to Rupert instead of CSGNet, which I realized when there were no comments on it. So here’s the forwarded version:
[From Rick Marken (2014.04.22.1450)]
Rupert Young (2014.04.22 18.00)
RY: The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
RM: This is a great question, Rupert! I would like to hear how some others would answer it before answering it myself. So I’ll wait a bit and see if anyone else replies. I would really like to see what others think is “wrong” with this picture (if anything) from a PCT perspective.
Best
Rick
–
Richard S. Marken PhD
www.mindreadings.com
It is difficult to get a man to understand something, when his salary depends upon his not understanding it. – Upton Sinclair
[From Fred Nickols (2014.04.23.0731 EDT)]
I looked at the diagram and the drawing and read portions of the paper. I’m not sure I can put my finger on anything wrong. If I substitute thermostat for governor and furnace for steam engine then it seems to me that the comparator is outside the thermostat/governor and I’m not sure that’s right. The thermostat turns on and off the furnace and the governor increases or decreases steam to the engine. But, I suspect Rupert sees something wrong, as do you, Rick, so I’m happy to be enlightened.
Fred Nickols
From: Richard Marken [mailto:rsmarken@gmail.com]
Sent: Tuesday, April 22, 2014 10:09 PM
To: csgnet@lists.illinois.edu
Subject: Fwd: What’s wrong with this picture?
[From Rick Marken(2014.04.22.1910)]
I sent this to Rupert instead of CSGNet, which I realized when there were no comments on it. So here’s the forwarded version:
[From Rick Marken (2014.04.22.1450)]
Rupert Young (2014.04.22 18.00)
RY: The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
<image002.jpg>
RM: This is a great question, Rupert! I would like to hear how some others would answer it before answering it myself. So I’ll wait a bit and see if anyone else replies. I would really like to see what others think is “wrong” with this picture (if anything) from a PCT perspective.
Best
Rick
–
Richard S. Marken PhD
www.mindreadings.com
It is difficult to get a man to understand something, when his salary depends upon his not understanding it. – Upton Sinclair
[Martin Taylor 2014.04.23.11.43]
I don't know why, but like Rick I sent my reply directly to Rupert
instead of to the list. Belatedly, here it is.
Martin
-------- Original Message --------
[Martin Taylor 2014.04.22.09.35]
There’s nothing wrong with the picture for what it wants to show,
assuming that the belt between the engine and the flyball pulley
is shown in the original. The “A” picture illustrates a feedback
loop whereby changes in the shaft velocity induce compensating
changes to bring the velocity back to where it was, and the “B”
figure suggests such a loop. It’s just uninformative and a bit
misleading if the B diagram is supposed to represent the A
picture. Let’s analyze what the system actually does according to
the “A” picture, and then see why the “B” diagram is misleading.
Let’s start with the shaft rotational velocity, since that’s what
is supposed to be controlled to match some reference velocity.
Where is the reference velocity set? Nothing in the “A” picture
shows a reference rpm input, which is clearly shown in the “B”
diagram. So there’s a mismatch between the halves of the figure
right off the bat.
However, let’s start with the rotational velocity anyway, and see
where it leads us. The engine torque together with the load (not
shown in the “A” diagram) determine the velocity. The engine
torque, and hence the rotational velocity, is increased by opening
the valve, which is done by moving the vertical link rod down. The
link rod is attached to the lever arm, so to increase the
velocity, the other end of the arm must go up. It goes up when the
flyballs rotate slowly, and the flyball speed is determined by the
shaft rotational velocity by means of the invisible belt. So if
the shaft is going slowly, the flyball speed moves the level arm
and the vertical link so as to make the engine go faster.
So far, so good. But what actually is being controlled here? It’s
hard to tell, because all the variables are being stabilized
around the loop, and there is no reference value setting for any
of them – or is there? It’s hard to tell from the A picture, but
it looks as though there are two adjustments. One is at the collar
that connects the left end of the lever to the top of the flyball
mechanism, and the other is the screw adjustment on the vertical
link rod. The first changes the offset relation between flyball
speed and lever angle. The second affects the offset relation
between lever angle and valve opening. These are human-operated
adjustments, which would be the outputs of some human control
system, presumably one that controls a perception of shaft
rotational velocity.
In a control system, there is an asymmetry between input and
output, which determines where in the loop is the controlled
variable. In this system, I see an analogue of a perceptual
function in the flywheel that translates the rotation speed into a
height of the collar to which the lever arm is attached. I see a
powerful output in the form of the engine that translates lever
arm position into rotary torque. I see the possibility for setting
a reference value for the height of the collar. So I would redraw
the “B” figure, perhaps like this, perhaps more simply:
The main differences between this figure and the actual “B” figure
are the introduction of the reference input between the flyball
and the motor, the inclusion of the load, and most importantly
recognition that the sensing and setting of the rpm is in a
different, higher-level, control unit, and is not an input to the
flyball. The actual speed of the shaft is an input to the flyball,
but that’s the only input to it. The controlled perception in the
loop depicted in the “A” figure is not the rotary speed – that’s
controlled in the human’s control system – but is the collar
height, or equivalently, the lever arm angle. To see this, just imagine how the behaviour of the system would
change if the flyball balls had some weight added, so that it took
a higher shaft rotational speed to spin the balls up to any given
height. What would be controlled to the same value after the
change – the collar height or the shaft speed? What would the
human controller do? He would adjust the link screw to bring the
speed for a given collar height back to where he wanted it, would
he not? That would be the normal action output of whatever control
unit actually controls the shaft speed, and in this case that
control unit is inside the human. It’s a nice example of a
two-level control system.
Martin
Subject:
Re: What’s wrong with this picture?
Date:
Wed, 23 Apr 2014 00:51:26 -0400
From:
Martin Taylor
To:
mmt-csg@mmtaylor.netrupert@moonsit.co.ukrupert@moonsit.co.uk
[Rupert Young (2014.04.22 18.00)]
The issue of "standard" control theory keeps coming up, asper the Cowan paper. Is there a reference for a paper or post
(if only there was a way organising the CSG posts so that one
on this topic could be easily located) for an in-depth
explanation of why that model is not right from a PCT
perspective?
If not, would someone like to say what is wrong with thispicture?
Regards,
Rupert
[Rupert Young (2014.04.26 16.00)]
That’s pretty much what I was thinking though you’ve put it clearly and filled in a few blanks of which I was unsure.
It is supposed to be controlling speed yet there is no speed sensor in either picture, though perhaps it is taken for granted in “B”, as Rick says. But for the governor itself there is no such sensor. The component that is sensing (perceiving) the speed is the human, perhaps via a meter of some sort. So “B” is missing the fundamental part of the system that makes it a speed controller. The governor itself does not control speed, but some physical arrangement; the collar height.
However, I am wondering if the governor on its own is a self-regulating system rather than a control system (all control systems are self-regulating but not all self-regulating systems are control systems), in that an equilibrium is maintained due to the physical configuration and interaction of the components. If I understand you correctly adding weight (disturbance) to the flyballs would affect the system so that the equilibrium would find a different value. In other words there is no variable maintained at a reference. This might be something like predator-prey ratio regulation and adding a new species would upset the equilibrium, but a new equilibrium would arise.
So, then, the only thing that is a control system within the steam engine speed system is the human?
Regards,
Rupert
(Martin Taylor 2014.04.22.09.35)
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
[Martin Taylor 2014.04.22.09.35]
There's nothing wrong with the picture for what it wants to show, assuming that the belt between the engine and the flyball pulley is shown in the original. The "A" picture illustrates a feedback loop whereby changes in the shaft velocity induce compensating changes to bring the velocity back to where it was, and the "B" figure suggests such a loop. It's just uninformative and a bit misleading if the B diagram is supposed to represent the A picture. Let's analyze what the system actually does according to the "A" picture, and then see why the "B" diagram is misleading.
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
However, let’s start with the rotational velocity anyway, and see where it leads us. The engine torque together with the load (not shown in the “A” diagram) determine the velocity. The engine torque, and hence the rotational velocity, is increased by opening the valve, which is done by moving the vertical link rod down. The link rod is attached to the lever arm, so to increase the velocity, the other end of the arm must go up. It goes up when the flyballs rotate slowly, and the flyball speed is determined by the shaft rotational velocity by means of the invisible belt. So if the shaft is going slowly, the flyball speed moves the level arm and the vertical link so as to make the engine go faster.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
In a control system, there is an asymmetry between input and output, which determines where in the loop is the controlled variable. In this system, I see an analogue of a perceptual function in the flywheel that translates the rotation speed into a height of the collar to which the lever arm is attached. I see a powerful output in the form of the engine that translates lever arm position into rotary torque. I see the possibility for setting a reference value for the height of the collar. So I would redraw the “B” figure, perhaps like this, perhaps more simply:
The main differences between this figure and the actual “B” figure are the introduction of the reference input between the flyball and the motor, the inclusion of the load, and most importantly recognition that the sensing and setting of the rpm is in a different, higher-level, control unit, and is not an input to the flyball. The actual speed of the shaft is an input to the flyball, but that’s the only input to it. The controlled perception in the loop depicted in the “A” figure is not the rotary speed – that’s controlled in the human’s control system – but is the collar height, or equivalently, the lever arm angle. To see this, just imagine how the behaviour of the system would change if the flyball balls had some weight added, so that it took a higher shaft rotational speed to spin the balls up to any given height. What would be controlled to the same value after the change – the collar height or the shaft speed? What would the human controller do? He would adjust the link screw to bring the speed for a given collar height back to where he wanted it, would he not? That would be the normal action output of whatever control unit actually controls the shaft speed, and in this case that control unit is inside the human. It’s a nice example of a two-level control system.
Martin
[Rupert Young (2014.04.22 18.00)]
The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
Regards,
Rupert
[From Adam Matic 2014.04.26 1300]
I guess hat is wrong with the picture is that it is missing the velocity sensor in the feedback path, right before the negative input.
Motor shaft velocity is proportional to ball velocity is proportional to height of the top part. I guess the current height of the top part is ‘perception’, and the limiting height a ‘reference’, since they are directly compared mechanically. Those two heights produce a mechanical error that is converted the change in the amount of fuel going to the motor (if I got that right).
The heights would be analog to neural signals, and we usually refer to neural controllers, such as tendon tension controller, by naming what the neural magnitude ‘perception’ represents.
Adam
On Sat, Apr 26, 2014 at 11:43 AM, rupert@moonsit.co.uk rupert@moonsit.co.uk wrote:
[Rupert Young (2014.04.26 16.00)]
(Martin Taylor 2014.04.22.09.35)
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
That’s pretty much what I was thinking though you’ve put it clearly and filled in a few blanks of which I was unsure.
It is supposed to be controlling speed yet there is no speed sensor in either picture, though perhaps it is taken for granted in “B”, as Rick says. But for the governor itself there is no such sensor. The component that is sensing (perceiving) the speed is the human, perhaps via a meter of some sort. So “B” is missing the fundamental part of the system that makes it a speed controller. The governor itself does not control speed, but some physical arrangement; the collar height.
However, I am wondering if the governor on its own is a self-regulating system rather than a control system (all control systems are self-regulating but not all self-regulating systems are control systems), in that an equilibrium is maintained due to the physical configuration and interaction of the components. If I understand you correctly adding weight (disturbance) to the flyballs would affect the system so that the equilibrium would find a different value. In other words there is no variable maintained at a reference. This might be something like predator-prey ratio regulation and adding a new species would upset the equilibrium, but a new equilibrium would arise.
So, then, the only thing that is a control system within the steam engine speed system is the human?
Regards,
Rupert
[Martin Taylor 2014.04.22.09.35]
[Rupert Young (2014.04.22 18.00)]
The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
Regards,
Rupert
There’s nothing wrong with the picture for what it wants to show, assuming that the belt between the engine and the flyball pulley is shown in the original. The “A” picture illustrates a feedback loop whereby changes in the shaft velocity induce compensating changes to bring the velocity back to where it was, and the “B” figure suggests such a loop. It’s just uninformative and a bit misleading if the B diagram is supposed to represent the A picture. Let’s analyze what the system actually does according to the “A” picture, and then see why the “B” diagram is misleading.
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
However, let’s start with the rotational velocity anyway, and see where it leads us. The engine torque together with the load (not shown in the “A” diagram) determine the velocity. The engine torque, and hence the rotational velocity, is increased by opening the valve, which is done by moving the vertical link rod down. The link rod is attached to the lever arm, so to increase the velocity, the other end of the arm must go up. It goes up when the flyballs rotate slowly, and the flyball speed is determined by the shaft rotational velocity by means of the invisible belt. So if the shaft is going slowly, the flyball speed moves the level arm and the vertical link so as to make the engine go faster.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
In a control system, there is an asymmetry between input and output, which determines where in the loop is the controlled variable. In this system, I see an analogue of a perceptual function in the flywheel that translates the rotation speed into a height of the collar to which the lever arm is attached. I see a powerful output in the form of the engine that translates lever arm position into rotary torque. I see the possibility for setting a reference value for the height of the collar. So I would redraw the “B” figure, perhaps like this, perhaps more simply:
The main differences between this figure and the actual “B” figure are the introduction of the reference input between the flyball and the motor, the inclusion of the load, and most importantly recognition that the sensing and setting of the rpm is in a different, higher-level, control unit, and is not an input to the flyball. The actual speed of the shaft is an input to the flyball, but that’s the only input to it. The controlled perception in the loop depicted in the “A” figure is not the rotary speed – that’s controlled in the human’s control system – but is the collar height, or equivalently, the lever arm angle.
To see this, just imagine how the behaviour of the system would change if the flyball balls had some weight added, so that it took a higher shaft rotational speed to spin the balls up to any given height. What would be controlled to the same value after the change – the collar height or the shaft speed? What would the human controller do? He would adjust the link screw to bring the speed for a given collar height back to where he wanted it, would he not? That would be the normal action output of whatever control unit actually controls the shaft speed, and in this case that control unit is inside the human. It’s a nice example of a two-level control system.
Martin
Isn’t it fascinating how we disagree! Like Adam I think that the Governor is closely analogous to a PCT unit. There are so many components that we haven’t explained. Surely then, the component of the governor that goes from it’s spinning velocity through to its vertical movement is its input function and the movements themselves are analogous to the neural signals like Adam says?
Warren
On Sat, Apr 26, 2014 at 11:43 AM, rupert@moonsit.co.uk rupert@moonsit.co.uk wrote:
[Rupert Young (2014.04.26 16.00)]
(Martin Taylor 2014.04.22.09.35)
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
That’s pretty much what I was thinking though you’ve put it clearly and filled in a few blanks of which I was unsure.
It is supposed to be controlling speed yet there is no speed sensor in either picture, though perhaps it is taken for granted in “B”, as Rick says. But for the governor itself there is no such sensor. The component that is sensing (perceiving) the speed is the human, perhaps via a meter of some sort. So “B” is missing the fundamental part of the system that makes it a speed controller. The governor itself does not control speed, but some physical arrangement; the collar height.
However, I am wondering if the governor on its own is a self-regulating system rather than a control system (all control systems are self-regulating but not all self-regulating systems are control systems), in that an equilibrium is maintained due to the physical configuration and interaction of the components. If I understand you correctly adding weight (disturbance) to the flyballs would affect the system so that the equilibrium would find a different value. In other words there is no variable maintained at a reference. This might be something like predator-prey ratio regulation and adding a new species would upset the equilibrium, but a new equilibrium would arise.
So, then, the only thing that is a control system within the steam engine speed system is the human?
Regards,
Rupert
[Martin Taylor 2014.04.22.09.35]
[Rupert Young (2014.04.22 18.00)]
The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
<image.png>
Regards,
Rupert
There’s nothing wrong with the picture for what it wants to show, assuming that the belt between the engine and the flyball pulley is shown in the original. The “A” picture illustrates a feedback loop whereby changes in the shaft velocity induce compensating changes to bring the velocity back to where it was, and the “B” figure suggests such a loop. It’s just uninformative and a bit misleading if the B diagram is supposed to represent the A picture. Let’s analyze what the system actually does according to the “A” picture, and then see why the “B” diagram is misleading.
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
However, let’s start with the rotational velocity anyway, and see where it leads us. The engine torque together with the load (not shown in the “A” diagram) determine the velocity. The engine torque, and hence the rotational velocity, is increased by opening the valve, which is done by moving the vertical link rod down. The link rod is attached to the lever arm, so to increase the velocity, the other end of the arm must go up. It goes up when the flyballs rotate slowly, and the flyball speed is determined by the shaft rotational velocity by means of the invisible belt. So if the shaft is going slowly, the flyball speed moves the level arm and the vertical link so as to make the engine go faster.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
In a control system, there is an asymmetry between input and output, which determines where in the loop is the controlled variable. In this system, I see an analogue of a perceptual function in the flywheel that translates the rotation speed into a height of the collar to which the lever arm is attached. I see a powerful output in the form of the engine that translates lever arm position into rotary torque. I see the possibility for setting a reference value for the height of the collar. So I would redraw the “B” figure, perhaps like this, perhaps more simply:
<image.jpeg>The main differences between this figure and the actual “B” figure are the introduction of the reference input between the flyball and the motor, the inclusion of the load, and most importantly recognition that the sensing and setting of the rpm is in a different, higher-level, control unit, and is not an input to the flyball. The actual speed of the shaft is an input to the flyball, but that’s the only input to it. The controlled perception in the loop depicted in the “A” figure is not the rotary speed – that’s controlled in the human’s control system – but is the collar height, or equivalently, the lever arm angle.
To see this, just imagine how the behaviour of the system would change if the flyball balls had some weight added, so that it took a higher shaft rotational speed to spin the balls up to any given height. What would be controlled to the same value after the change – the collar height or the shaft speed? What would the human controller do? He would adjust the link screw to bring the speed for a given collar height back to where he wanted it, would he not? That would be the normal action output of whatever control unit actually controls the shaft speed, and in this case that control unit is inside the human. It’s a nice example of a two-level control system.
Martin
Hi Warren,
With whom and with what are you disagreeing?
Regards
Rupert
On Sat, Apr 26, 2014 at 11:43 AM, rupert@moonsit.co.uk rupert@moonsit.co.uk wrote:
[Rupert Young (2014.04.26 16.00)]
(Martin Taylor 2014.04.22.09.35)
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
That’s pretty much what I was thinking though you’ve put it clearly and filled in a few blanks of which I was unsure.
It is supposed to be controlling speed yet there is no speed sensor in either picture, though perhaps it is taken for granted in “B”, as Rick says. But for the governor itself there is no such sensor. The component that is sensing (perceiving) the speed is the human, perhaps via a meter of some sort. So “B” is missing the fundamental part of the system that makes it a speed controller. The governor itself does not control speed, but some physical arrangement; the collar height.
However, I am wondering if the governor on its own is a self-regulating system rather than a control system (all control systems are self-regulating but not all self-regulating systems are control systems), in that an equilibrium is maintained due to the physical configuration and interaction of the components. If I understand you correctly adding weight (disturbance) to the flyballs would affect the system so that the equilibrium would find a different value. In other words there is no variable maintained at a reference. This might be something like predator-prey ratio regulation and adding a new species would upset the equilibrium, but a new equilibrium would arise.
So, then, the only thing that is a control system within the steam engine speed system is the human?
Regards,
Rupert
[Martin Taylor 2014.04.22.09.35]
[Rupert Young (2014.04.22 18.00)]
The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
<image.png>
Regards,
Rupert
There’s nothing wrong with the picture for what it wants to show, assuming that the belt between the engine and the flyball pulley is shown in the original. The “A” picture illustrates a feedback loop whereby changes in the shaft velocity induce compensating changes to bring the velocity back to where it was, and the “B” figure suggests such a loop. It’s just uninformative and a bit misleading if the B diagram is supposed to represent the A picture. Let’s analyze what the system actually does according to the “A” picture, and then see why the “B” diagram is misleading.
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
However, let’s start with the rotational velocity anyway, and see where it leads us. The engine torque together with the load (not shown in the “A” diagram) determine the velocity. The engine torque, and hence the rotational velocity, is increased by opening the valve, which is done by moving the vertical link rod down. The link rod is attached to the lever arm, so to increase the velocity, the other end of the arm must go up. It goes up when the flyballs rotate slowly, and the flyball speed is determined by the shaft rotational velocity by means of the invisible belt. So if the shaft is going slowly, the flyball speed moves the level arm and the vertical link so as to make the engine go faster.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
In a control system, there is an asymmetry between input and output, which determines where in the loop is the controlled variable. In this system, I see an analogue of a perceptual function in the flywheel that translates the rotation speed into a height of the collar to which the lever arm is attached. I see a powerful output in the form of the engine that translates lever arm position into rotary torque. I see the possibility for setting a reference value for the height of the collar. So I would redraw the “B” figure, perhaps like this, perhaps more simply:
<image.jpeg>The main differences between this figure and the actual “B” figure are the introduction of the reference input between the flyball and the motor, the inclusion of the load, and most importantly recognition that the sensing and setting of the rpm is in a different, higher-level, control unit, and is not an input to the flyball. The actual speed of the shaft is an input to the flyball, but that’s the only input to it. The controlled perception in the loop depicted in the “A” figure is not the rotary speed – that’s controlled in the human’s control system – but is the collar height, or equivalently, the lever arm angle.
To see this, just imagine how the behaviour of the system would change if the flyball balls had some weight added, so that it took a higher shaft rotational speed to spin the balls up to any given height. What would be controlled to the same value after the change – the collar height or the shaft speed? What would the human controller do? He would adjust the link screw to bring the speed for a given collar height back to where he wanted it, would he not? That would be the normal action output of whatever control unit actually controls the shaft speed, and in this case that control unit is inside the human. It’s a nice example of a two-level control system.
Martin
Not just me. Sorry for being ambiguous. I was saying it is fascinating how we are all coming up with different mappings of the Governor onto the components a PCT control unit.
Warren
On Sat, Apr 26, 2014 at 11:43 AM, rupert@moonsit.co.uk rupert@moonsit.co.uk wrote:
[Rupert Young (2014.04.26 16.00)]
(Martin Taylor 2014.04.22.09.35)
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
That’s pretty much what I was thinking though you’ve put it clearly and filled in a few blanks of which I was unsure.
It is supposed to be controlling speed yet there is no speed sensor in either picture, though perhaps it is taken for granted in “B”, as Rick says. But for the governor itself there is no such sensor. The component that is sensing (perceiving) the speed is the human, perhaps via a meter of some sort. So “B” is missing the fundamental part of the system that makes it a speed controller. The governor itself does not control speed, but some physical arrangement; the collar height.
However, I am wondering if the governor on its own is a self-regulating system rather than a control system (all control systems are self-regulating but not all self-regulating systems are control systems), in that an equilibrium is maintained due to the physical configuration and interaction of the components. If I understand you correctly adding weight (disturbance) to the flyballs would affect the system so that the equilibrium would find a different value. In other words there is no variable maintained at a reference. This might be something like predator-prey ratio regulation and adding a new species would upset the equilibrium, but a new equilibrium would arise.
So, then, the only thing that is a control system within the steam engine speed system is the human?
Regards,
Rupert
[Martin Taylor 2014.04.22.09.35]
[Rupert Young (2014.04.22 18.00)]
The issue of “standard” control theory keeps coming up, as per the Cowan paper. Is there a reference for a paper or post (if only there was a way organising the CSG posts so that one on this topic could be easily located) for an in-depth explanation of why that model is not right from a PCT perspective?
If not, would someone like to say what is wrong with this picture?
<image.png>
Regards,
Rupert
There’s nothing wrong with the picture for what it wants to show, assuming that the belt between the engine and the flyball pulley is shown in the original. The “A” picture illustrates a feedback loop whereby changes in the shaft velocity induce compensating changes to bring the velocity back to where it was, and the “B” figure suggests such a loop. It’s just uninformative and a bit misleading if the B diagram is supposed to represent the A picture. Let’s analyze what the system actually does according to the “A” picture, and then see why the “B” diagram is misleading.
Let’s start with the shaft rotational velocity, since that’s what is supposed to be controlled to match some reference velocity. Where is the reference velocity set? Nothing in the “A” picture shows a reference rpm input, which is clearly shown in the “B” diagram. So there’s a mismatch between the halves of the figure right off the bat.
However, let’s start with the rotational velocity anyway, and see where it leads us. The engine torque together with the load (not shown in the “A” diagram) determine the velocity. The engine torque, and hence the rotational velocity, is increased by opening the valve, which is done by moving the vertical link rod down. The link rod is attached to the lever arm, so to increase the velocity, the other end of the arm must go up. It goes up when the flyballs rotate slowly, and the flyball speed is determined by the shaft rotational velocity by means of the invisible belt. So if the shaft is going slowly, the flyball speed moves the level arm and the vertical link so as to make the engine go faster.
So far, so good. But what actually is being controlled here? It’s hard to tell, because all the variables are being stabilized around the loop, and there is no reference value setting for any of them – or is there? It’s hard to tell from the A picture, but it looks as though there are two adjustments. One is at the collar that connects the left end of the lever to the top of the flyball mechanism, and the other is the screw adjustment on the vertical link rod. The first changes the offset relation between flyball speed and lever angle. The second affects the offset relation between lever angle and valve opening. These are human-operated adjustments, which would be the outputs of some human control system, presumably one that controls a perception of shaft rotational velocity.
In a control system, there is an asymmetry between input and output, which determines where in the loop is the controlled variable. In this system, I see an analogue of a perceptual function in the flywheel that translates the rotation speed into a height of the collar to which the lever arm is attached. I see a powerful output in the form of the engine that translates lever arm position into rotary torque. I see the possibility for setting a reference value for the height of the collar. So I would redraw the “B” figure, perhaps like this, perhaps more simply:
<image.jpeg>The main differences between this figure and the actual “B” figure are the introduction of the reference input between the flyball and the motor, the inclusion of the load, and most importantly recognition that the sensing and setting of the rpm is in a different, higher-level, control unit, and is not an input to the flyball. The actual speed of the shaft is an input to the flyball, but that’s the only input to it. The controlled perception in the loop depicted in the “A” figure is not the rotary speed – that’s controlled in the human’s control system – but is the collar height, or equivalently, the lever arm angle.
To see this, just imagine how the behaviour of the system would change if the flyball balls had some weight added, so that it took a higher shaft rotational speed to spin the balls up to any given height. What would be controlled to the same value after the change – the collar height or the shaft speed? What would the human controller do? He would adjust the link screw to bring the speed for a given collar height back to where he wanted it, would he not? That would be the normal action output of whatever control unit actually controls the shaft speed, and in this case that control unit is inside the human. It’s a nice example of a two-level control system.
Martin
[Martin Taylor 2014.04.26.09.33]
[Rupert Young (2014.04.26 16.00)]
That's pretty much what I was thinking though you've put itclearly and filled in a few blanks of which I was unsure.
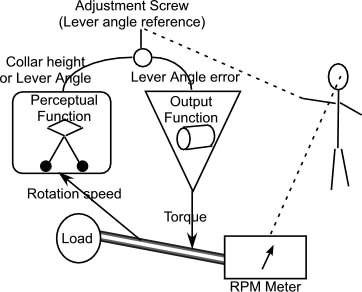
It is supposed to be controlling speed yet there is no speedsensor in either picture, though perhaps it is taken for granted
in “B”, as Rick says. But for the governor itself there is no
such sensor. The component that is sensing (perceiving) the
speed is the human, perhaps via a meter of some sort. So “B” is
missing the fundamental part of the system that makes it a speed
controller. The governor itself does not control speed, but some
physical arrangement; the collar height.
However, I am wondering if the governor on its own is aself-regulating system rather than a control system (all control
systems are self-regulating but not all self-regulating systems
are control systems), in that an equilibrium is maintained due
to the physical configuration and interaction of the components.
I'm getting quite uncertain as to what is meant by a
“self-regulating system”. So I can’t answer you directly. But if I
substitute “negative feedback loop”, I quite agree. Not all negative
feedback loops are control systems. However, even in control loops,
“equilibrium is maintained due to the physical configuration and
interaction of the components.”
What distinguishes the class of control systems from other negative
feedback loops is the distribution of energy gain. The perceiving
side of a control loop is, ideally, a zero-energy area. Of course it
does take some energy, either provided by the environment (photons,
for example) or internally (chemistry that drives nerve impulses).
The output side, on the other hand, uses an external energy source
to deliver sufficient energy to the environment to enable the
control loop to counter the energy of disturbances. You don’t
necessarily see the use of this external energy supply at any
particular point in a complex circuit, except that in a control
system it must occur between the computation of the error value and
the point where the disturbance acts.
In the case of the flyball governor, the only external energy source
is the fuel to the steam engine. The disturbance is a variable load
that would, in the absence of the engine, set the rotational speed
– possibly at zero, but maybe not, if the load has its own rotary
drive. Thinking of the circuit flow, any energy that drives the
flyball comes from what is left AFTER the disturbance, and it takes
only a small amount of energy to change the rotational speed of the
flyball. In fact, the flyball need not consist of massive weights.
It could be microscopic (or even nanoscopic) provided that its
effect is eventually to change the steam valve opening, an action
that also takes very little energy compared to the energy output of
the steam engine.
The disparity between the energy requirements of the flyball side of
the circuit and the steam-engine side is what makes this circuit a
control system as opposed to a generic negative feedback loop.
If I understand you correctly adding weight (disturbance) tothe flyballs would affect the system so that the equilibrium
would find a different value.
That's correct.
In other words there is no variable maintained at areference.
Yes there is. On the flyball side, you could call it the swing
radius of the flyballs or the collar level or the lever arm angle,
all of which change together as the rotary shaft speed changes. If
the steam engine power changes or the load changes, these variables
all change so as to bring the rotary speed back (nearly) to the
reference value.
This might be something like predator-prey ratio regulationand adding a new species would upset the equilibrium, but a
new equilibrium would arise.
Something like, yes, in the sense that the predator-prey system is a
negative feedback loop, and if the flyball and steam valve
relationships to the values they influence were sufficiently
nonlinear, I suppose the flyball system might oscillate or even hunt
chaotically rather than stabilize at some rotary speed (I haven’t
checked this possibility, so it might not occur). And I suppose
there is an asymmetry in the predator-prey relation, in that the
predator gets its energy from the prey whereas the prey gets its
from parts of its external environment that don’t include the
predator. But again, I haven’t followed this through to see how real
the analogy might be. Personally, I find the analogy more misleading
than helpful.
So, then, the only thing that is a control system within thesteam engine speed system is the human?
No, that doesn't follow. The lever arm angle is controlled, and the
reference value for that control is set by the human.
I think one of the problems with conceiving this system is a problem
generic to all two-level systems that have only one control unit at
each level. The problem is that there is only one environmental and
perceptual variable at the lower level, and therefore the perceptual
variable at the upper level is a function of the same environmental
variable. Functionally, if the perceptual variable at level 1 is
P1(input) (collar height = P(rotary speed)), then the perceptual
variable at level 2 is P2(P1(input)) , which can be written as a
single function P12(input), which means that from outside it looks
as though level 2 is controlling a direct perception of the input
(although in the flyball case, we think the human perceives the
rotary speed through a different channel). It is, but the mechanism
of that control is by providing a reference value to the lower
level, not by acting in the environment. Hence, any experiment with
a single environmental variable that the subject can influence will
give results that will not be easy to use for discriminating between
single-level and multi-level control structures.
Martin
(Martin Taylor
2014.04.22.09.35)
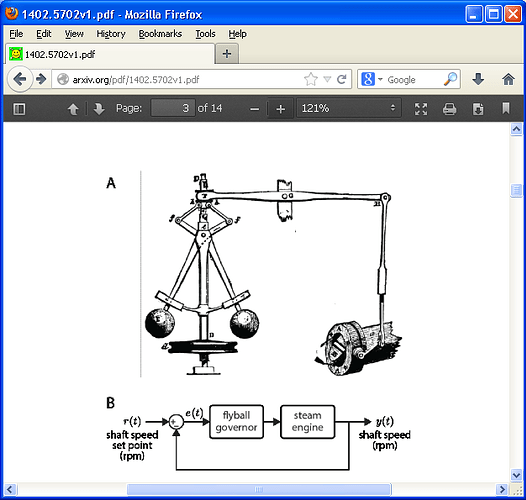
Let's start with the shaft
rotational velocity, since that’s what is supposed to be
controlled to match some reference velocity. Where is the
reference velocity set? Nothing in the “A” picture shows a
reference rpm input, which is clearly shown in the “B”
diagram. So there’s a mismatch between the halves of the
figure right off the bat.
So far, so good. But what
actually is being controlled here? It’s hard to tell,
because all the variables are being stabilized around the
loop, and there is no reference value setting for any of
them – or is there? It’s hard to tell from the A picture,
but it looks as though there are two adjustments. One is at
the collar that connects the left end of the lever to the
top of the flyball mechanism, and the other is the screw
adjustment on the vertical link rod. The first changes the
offset relation between flyball speed and lever angle. The
second affects the offset relation between lever angle and
valve opening. These are human-operated adjustments, which
would be the outputs of some human control system,
presumably one that controls a perception of shaft
rotational velocity.
[Richard Kennaway (20140427 20:24 BST)]
[Rupert Young (2014.04.26 16.00)]
It is supposed to be controlling speed yet there is no speed sensor in either picture, though perhaps it is taken for granted in "B", as Rick says. But for the governor itself there is no such sensor. The component that is sensing (perceiving) the speed is the human, perhaps via a meter of some sort. So "B" is missing the fundamental part of the system that makes it a speed controller. The governor itself does not control speed, but some physical arrangement; the collar height.
However, I am wondering if the governor on its own is a self-regulating system rather than a control system (all control systems are self-regulating but not all self-regulating systems are control systems), in that an equilibrium is maintained due to the physical configuration and interaction of the components. If I understand you correctly adding weight (disturbance) to the flyballs would affect the system so that the equilibrium would find a different value. In other words there is no variable maintained at a reference. This might be something like predator-prey ratio regulation and adding a new species would upset the equilibrium, but a new equilibrium would arise.
So, then, the only thing that is a control system within the steam engine speed system is the human?
I think this is overthinking the matter. The picture of the steam governor is annotated with letters that are presumably explained in the original source (but have been omitted from the paper under discussion). I guess that the wheel at the bottom of the vertical governor shaft would be connected by a belt drive to the shaft of the steam engine. That is the speed sensor.
The reference speed is set by the operator, probably by some adjustment of the connection between the horizontal beam and the governor, which changes the relationship between the ball separation and the steam valve.
The actuator is the steam valve, and the source of energy that the governor draws on to keep the shaft turning at the reference speed is the steam pressurised by the heat of burning fuel. This is a control system. The drawing on a source of energy is what distinguishes a control system from a ball-in-a-bowl passive equilibrium.
But it doesn't matter exactly where you draw imaginary lines to separate the "sensor", the "controller", the "output signal", and the "actuator". The angular separation of the balls could be taken as the "sensor" instead of the governor shaft speed. I don't think that's a good idea (because due to the inertia of the balls the relationship between separation and shaft speed is rather complicated), but good or bad, the system does not care and operates in exactly the same way, whatever you call its components.
The human operator is setting the reference speed. He will be doing so as his "behaviour", in order to control some perception. That perception could be the speed of the shaft (e.g. as read from a speedometer), but I expect it would typically be the proper operation of whatever apparatus the steam engine is driving.
-- Richard
--
Richard Kennaway, R.Kennaway@uea.ac.uk, Richard Kennaway
School of Computing Sciences,
University of East Anglia, Norwich NR4 7TJ, U.K.
[From Rick Marken (2009.07.20.2220)]
Here's a diagram of a control system from a textbook on control theory
for behavioral scientists. I found this as I was looking for
background material for another paper I'm writing on the failure of
the input-output model, which is the basis of conventional
psychological science. The diagram and derivation that goes along
with it are interesting because it seems like control theory is being
used to justify the input-output model, quite the opposite of the way
I use control theory in my _Revolution_ paper. So what gives?
According to the control system diagram and derivation variations in
system output are driven by variations in a reference variable. From
the diagram, the reference seems to be the input to the system,
although it's not clear what is system and what is environment in the
diagram. So this diagram seem to be trying to show that variations in
behavior (output) depend on variations in reference signal (input),
which is perfectly consistent with the input-output model of behavior.
There is a problem with the diagram and/or the derivation. I wonder if
anyone can spot it (not you Bill;-)
Best
Rick
Content-Type: image/gif; name="Graph.gif"
Content-Disposition: attachment; filename="Graph.gif"
X-Attachment-Id: f_fxdy41va0
Well, in my rather benighted view, there's a lot wrong with it. If the "Attender" is an "effector" and not the entire person, reference as input and error as input are okay with me even though the comparator has been reduced to that little circle. The big glitch, for me, is the way the disturbance has been incorporated into output and the controlled variable is either missing altogether, or if it is there, it consists of that other little circle and thus the controlled variable has been folded into output. In short, I think it's all wrong.
--
Regards,
Fred Nickols
Managing Partner
Distance Consulting, LLC
nickols@att.net
www.nickols.us
"Assistance at A Distance"
-------------- Original message ----------------------
From: Richard Marken <rsmarken@GMAIL.COM>
[From Rick Marken (2009.07.20.2220)]
Here's a diagram of a control system from a textbook on control theory
for behavioral scientists. I found this as I was looking for
background material for another paper I'm writing on the failure of
the input-output model, which is the basis of conventional
psychological science. The diagram and derivation that goes along
with it are interesting because it seems like control theory is being
used to justify the input-output model, quite the opposite of the way
I use control theory in my _Revolution_ paper. So what gives?According to the control system diagram and derivation variations in
system output are driven by variations in a reference variable. From
the diagram, the reference seems to be the input to the system,
although it's not clear what is system and what is environment in the
diagram. So this diagram seem to be trying to show that variations in
behavior (output) depend on variations in reference signal (input),
which is perfectly consistent with the input-output model of behavior.There is a problem with the diagram and/or the derivation. I wonder if
anyone can spot it (not you Bill;-)Best
Rick
[From Dick Robertson. 2009.07.21.0957CDT]
[From Rick Marken (2009.07.20.2220)]
Well, for one thing (among others) the error is derived from the reference and an unlabeled quantity to which the disturbance and attendant (?) contributes, but if this is supposed to be the perceptual variable how is the output contributing to it, instead of flying off into space as it does in the diagram?
Rick,
Would it be hard for you to program a simple tracking task according to their formulation? Of course it wouldn’t work, but they should see their theory applied and compared with a PCT built tracking task.
Best,
Dick R
[From Bill Powers (2009.07.21.1345 MDT)]
From Dick Robertson. 2009.07.21.0957CDT] --
Rick,
Would it be hard for you to program a simple tracking task according to their formulation? Of course it wouldn't work, but they should see their theory applied and compared with a PCT built tracking task.
Unfortunately, it would work. The place where the feedback signal departs from the output line is where we would put a feedback function, an input quantity, and an input function. As drawn, this diagram implies that the feedback function is a multiplier of 1 and the input function is also a multiplier of 1. We use those values quite often for convenience.
What is missing from this diagram is the output of the control system. That's hard to see until you know what control engineers mean by the term "output". They do not mean the actual physical output of the control system: the heat flowing from the furnace operated by a thermostat, the torque in the shaft of the motor that works the accelerator in a cruise control, and so on. They mean what we call the controlled variable. They say that the output of a thermostat is a controlled temperature of the room. The output of a cruise control is a constant speed of a car. The output of the iris reflex control system is a constant illumination of the retina (and how they can use the term output for that is beyond me, when it's clearly an input).
Years ago we had an Israeli control engineer on CSGnet. He absolutely refused to think of the controlled temperature of a room as an input to the control system, the thermostat, and left the list because we wouldn't agree. To him, the temperature was the whole purpose of the control system: it was what the thermostat did. The thermostat produced a constant temperature, so that was the thermostat's output. That's how they use these terms in engineering control theory, though I've never encountered such absolute refusal to understand our way of seeing it before. Look at Norbert Wiener's diagram of a control system (Fig. 4 in Chapter IV: Feedback and Oscillation). He does show a box in the feedback path, labeled "Feedback Take-off", but didn't realize that the signal coming out of it could be some function of the signal going into it, so the perceptual signal could be different from the physical output of the control system. Wiener clearly got his diagram from control engineers. That diagram has been around a long time. I think it kept cyberneticists from inventing PCT.
In engineering texts you will find cases in which there is an input function in the feedback path, but its output is not called a perceptual signal and there is no realization that the perceptual signal is what is controlled. My way of drawing a control system makes explicit all the details that the engineering version compresses into the dot where two lines join. Otherwise, my math is the same as the control engineer's math, but control engineers have a very strange concept of what control is. They don't look at it from the point of view of the control system, and that is essential.
Best,
Bill P.
[From Rick Marken (2009.07.21.1620)]
Bill Powers (2009.07.21.1345 MDT)
Unfortunately, it would work. The place where the feedback signal departs from the output line is where we would put a feedback function, an input quantity, and an input function. As drawn, this diagram implies that the feedback function is a multiplier of 1 and the input function is also a multiplier of 1. We use those values quite often for convenience.
Hey, you weren’t supposed to answer;-) But, of course, you’ve put your finger right on it: the Output variable in the diagram is actually the controlled variable. The actual output of the system is the unlabeled line coming out the the Attended, box, which is (Error X G) in the derivation. Equation 4 of the derivation shows that in a control system with high loop gain (large G) the controlled variable (Output in this diagram) is kept nearly equal to the Reference variable, protected from disturbance. As you note, this is a (static) analysis of a control system from the point of view of the user of the system. Indeed, it’s a diagram of a thermostat control system. The Reference variable is equivalent to the temperature setting of the thermostat and the Output variable is equivalent to the temperature of the room. So as the user of the thermostat moves the Reference setting (slowly) from, say, 60 to 80 degrees F, the room temperature will follow along, going for 60 to 80 degrees F, protected from disturbances such as variations in outside air temperature.
The fact that the closed loop analysis shown in the derivation is perfectly correct reinforces a point I have made earlier about PCT: the contribution of PCT is not the application of control theory analysis to understanding behavior. Rather, the contribution of PCT is the correct mapping of control theory to actual behavior. It’s making clear that, in organisms, the reference variable is inside the system, as an efferent neural signal. And the variable that is controlled – the Output variable in the derivation – is actually a perceived consequence of the results of an organisms actual outputs (actions) combined with the effects of independent influences on (disturbances to) the results of those actions. That is, what is controlled is an input variable, not an output variable. Behavior is the control of input, not output.
It’s interesting, of course, that the mapping of control to behavioral variables in this derivation seems perfectly consistent with the input-output model of conventional behavioral science. But the really interesting question to me is: Why did the authors of this diagram/derivation, who are behavioral scientists, use this mapping? Why, in other words, did they imply in their diagram that the Reference variable is an external input variable and the controlled input variable is an Output variable? Was it carelessness? Or was it done because they were predisposed to see this mapping because it is consistent with their existing beliefs about how behavior is organized? Or was it done because they could not conceive of an alternative mapping? Or was it done for some other reason that I can’t think of at the moment? Only the shadow knows.
Best
Rick
–
Richard S. Marken PhD
rsmarken@gmail.com
[From Bill Powers (2009.07.21.1939 MDT)]
Rick Marken (2009.07.21.1620) --
RM: Hey, you weren't supposed to answer;-)
BP: I thought I waited long enough for those who were going to reply to do so. But I guess I'm too impatient.
...
RM: But the really interesting question to me is: Why did the authors of this diagram/derivation, who are behavioral scientists, use this mapping? Why, in other words, did they imply in their diagram that the Reference variable is an external input variable and the controlled input variable is an Output variable? Was it carelessness? Or was it done because they were predisposed to see this mapping because it is consistent with their existing beliefs about how behavior is organized?
BP: I think it was simply because control engineers told them that this is how control systems work. It is quite correct if you're thinking of a customer who wants you to build a control system to control something he wants controlled. You give him a box with a knob on it, which allows the customer to input reference-level settings, and the wires coming out of the box operate some motors or furnaces or valves that produce the output the customer wanted to control with the knob. Just think of how a cruise control works. You input the reference speed by clicking the lever when the speedometer indicates the speed you want. Then the control box somehow operates the engine, producing the speed you selected. A nice simple input-output system, if you know nothing about how it works.
RM: Or was it done because they could not conceive of an alternative mapping? Or was it done for some other reason that I can't think of at the moment? Only the shadow knows.
BP: I think it was just because they knew nothing about control and believed whatever the engineers told them, and were happy if they understood half of it.
Best,
Bill P.
Hey Rick
can you give me the actual formulas for calucating the
·
Perceptual
Signal
·
Input
quantity (controlled variable)
·
Output
Quantity
·
Feedback
Quantity
·
Error
Signal
I want to put it on a spreadsheet and play
with it a bit. I have the demo but I would like a get a better feel. ( I
actually think the demo in the latest book is great, now I’m beginning to
get some where at long last, this book will go a long way to getting buy-in
to PCT).
Best
Gavin
Network (CSGnet) [mailto:CSGNET@LISTSERV.ILLINOIS.EDU] On Behalf Of Richard Marken
July 2009 11:18 a.m.
this picture?
[From Rick Marken
(2009.07.21.1620)]
Bill Powers
(2009.07.21.1345 MDT)Unfortunately, it would work. The place where the feedback signal departs from
the output line is where we would put a feedback function, an input quantity,
and an input function. As drawn, this diagram implies that the feedback
function is a multiplier of 1 and the input function is also a multiplier of 1.
We use those values quite often for convenience.
Hey, you weren’t supposed to answer;-) But, of course, you’ve put your finger
right on it: the Output variable in the diagram is actually the controlled
variable. The actual output of the system is the unlabeled line coming out the
the Attended, box, which is (Error X G) in the derivation. Equation 4 of the
derivation shows that in a control system with high loop gain (large G) the
controlled variable (Output in this diagram) is kept nearly equal to the
Reference variable, protected from disturbance. As you note, this is a
(static) analysis of a control system from the point of view of the user of the
system. Indeed, it’s a diagram of a thermostat control system. The Reference
variable is equivalent to the temperature setting of the thermostat and the
Output variable is equivalent to the temperature of the room. So as the user of
the thermostat moves the Reference setting (slowly) from, say, 60 to 80 degrees
F, the room temperature will follow along, going for 60 to 80 degrees F,
protected from disturbances such as variations in outside air temperature.
The fact that the closed loop analysis shown in the derivation is
perfectly correct reinforces a point I have made earlier about PCT: the
contribution of PCT is not the application of control theory analysis to
understanding behavior. Rather, the contribution of PCT is the correct mapping
of control theory to actual behavior. It’s making clear that, in organisms, the
reference variable is inside the system, as an efferent neural signal. And
the variable that is controlled – the Output variable in the derivation – is
actually a perceived consequence of the results of an organisms actual outputs
(actions) combined with the effects of independent influences on (disturbances
to) the results of those actions. That is, what is controlled is an input
variable, not an output variable. Behavior is the control of input, not output.
It’s interesting, of course, that the mapping of control to behavioral
variables in this derivation seems perfectly consistent with the input-output
model of conventional behavioral science. But the really interesting question
to me is: Why did the authors of this diagram/derivation, who are behavioral
scientists, use this mapping? Why, in other words, did they imply in their
diagram that the Reference variable is an external input variable and the
controlled input variable is an Output variable? Was it carelessness? Or was it
done because they were predisposed to see this mapping because it is consistent
with their existing beliefs about how behavior is organized? Or was it done
because they could not conceive of an alternative mapping? Or was it done for
some other reason that I can’t think of at the moment? Only the shadow knows.
Best
Rick
Richard S. Marken PhD
rsmarken@gmail.com
[From Rick Marken (2009.07.21.2245)]
ControlModel.xls (16 KB)
On Tue, Jul 21, 2009 at 7:15 PM, Gavin Ritz garritz@xtra.co.nz wrote:
Hey Rick
can you give me the actual formulas for calucating the
·
Perceptual
Signal
·
Input
quantity (controlled variable)
·
Output
Quantity
·
Feedback
Quantity
·
Error
Signal
I’ve attached a little spreadsheet model that I just cobbled together. It shows how the controlled variable (which I see as equivalent to the perceptual signal) is defined by the perceptual function. I’ve picked a very simple perceptual function: a linear combination of three scalar physical variables, two of which can vary independent of the actions of the system and are thus called “disturbances”; and one of which is the physical output of the system, which represents the feedback effect of the system’s output on it’s input. The output function is a pure integrator. I’ve shown text versions of both the perceptual and output functions; the actual functions are in the cells that do the computations: the perceptual function is computed in the cell that produces the value of the controlled variable; the output function is computer in the cell that produces the value of the output variable.
The spreadsheet uses automatic calculation so if you enter a new value for the reference (the blue cell to the right of “Reference”) the spreadsheet will very quickly iterate to produce an output that brings the controlled variable into a match with the reference. So by typing different values for the reference you can see that the control system quickly brings the controlled perceptual variable into a match with it. You can also type in new values for the disturbance variables (the two blue cells above the word “Disturbances”). Note that however these values are changed, the output varies so as to keep the controlled variable matching the reference.
The blue cells are the only ones into which you can enter new numbers without potentially screwing up the behavior of the control system. I’ve highlighted the controlled variable cell in rose color just so it’s easy to compare this value to the reference value (in blue) above it. However, you can certainly play around with this a bit. The most drastic (and interesting) changes would be to the perceptual or output functions. Changes to these could make the system unstable (and, thus, go into a positive feedback, runaway regime). But you can always leave the sheet without saving it so don’t worry about breaking it;-)
Have a ball.
Best
Richard S. Marken PhD
rsmarken@gmail.com