Hi Adam
RM: The behavioral illusion is that the function relating d to o (independent to dependent variable in research) is a characteristic of the organism when, in fact, it is the inverse of the feedback connection from output, o, to the controlled variable, qi, to which d is a disturbance.
AM: Yes. Glad we agree, then.
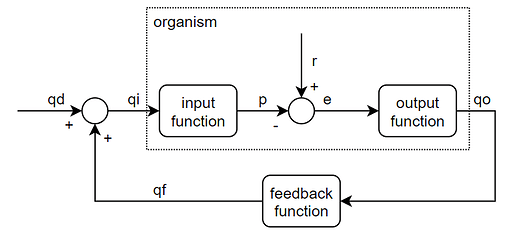
AM: (though, the feedback function relates qo to to qf in a living control system)
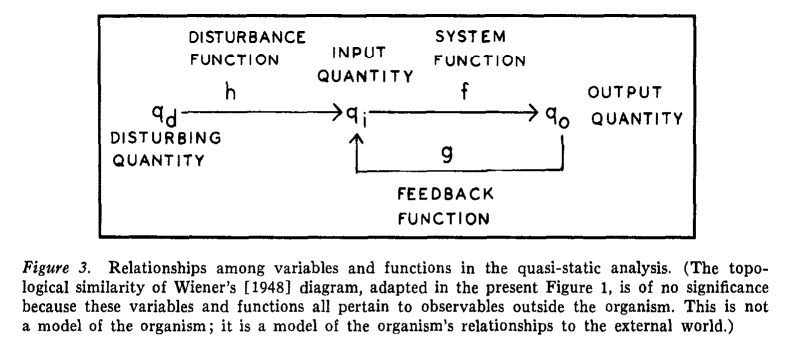
RM: Then we don’t agree. The feedback function relates qo to qi, output to controlled variable. The qf variable that you inserted in the PCT diagram below conceals this very important fact from both your readers and yourself. I will explain below why it’s important to understand that the feedback function relates qo to qi and not qo to qf.
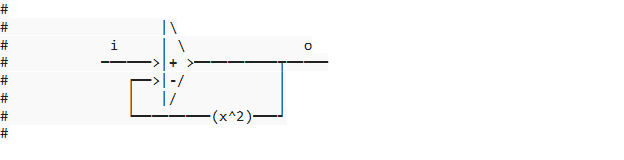
RM: Yes, but the input-output function you are talking about is not the one that is illusory. The problem with your analysis is that the labelings in your square root calculator are quite misleading with respect to how PCT maps control theory to living systems.
AM: That demo is not meant to represent a living control system, and the labels don’t match, but the setup is analogous to any feedback system.
RM: But it is quite misleading. One of the main things that distinguishes PCT from other applications of control theory to behavior – and control theory was being used as a model of behavior well before Powers came along (as noted in the 1978 paper in the discussion of the “Input blunder”) – is how it maps control theory to behavior. While it’s true that the map is not the territory, a distorted map can eliminate any chance of your finding the treasure hidden in that territory.
AM: The input i in the demo would be equivalent to the reference signal, entering the comparator / amplifier with a positive sign. The other input to the comparator would be equivalent to the perceptual signal, entering with the negative sign. The simulated comparator first finds the error, then multiplies with gain, then adds the error to a leaky integrator, so the output o of the comparator is something like the behavioral output, but not quite.
RM: This way of mapping it rather effectively hides the behavioral illusion. In order to uncover the behavioral illusion from your simulation you have to see the variable i as an independent variable having an effect on a controlled variable. So the comparator in the simulation has to be seen as a perceptual function. And you have to know that qo^2, not qo, is the variable that enters the perceptual function along with i. Only after you get that rather significant amount of remapping done can you can see that the the square root relationship between i (disturbance) and qo (system output) is the behavioral illusion.
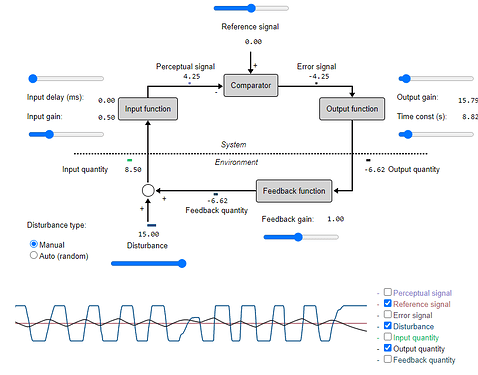
AM: For clarity, we can expand it to full pct diagram, replacing system function f from Bill’s diagram with the organism.
RM: Yes, that’s a much clearer way of describing things. Except for that added qf variable. That little addition screws it up big time.
AM: The qd-qo function will depend very little on the upper forward path,
RM: In fact, the qd-qo or S-R relationship depends not at all on the forward function. The relationship between qd and qo depends only on the nature of the connection between qo and qi. The qf in your diagram is what Powers calls g(qo) where g() is the feedback function connecting qo to qi. The derivation of the “behavioral illusion” equation:
qo = g-1 [qi* - h(qd] (1) (unnumbered equation in Powers, 1978)
is based on the assumption that
qi = g(qo) + h(qd) (2) (also equation 2 in Powers , 1978)
RM: There is no variable qf in Bill’s analysis. So why is it important to know that the behavioral illusion turns on the fact that control system output, qo, affects the controlled variable, qi, and not your variable, qf, which is equivalent to the output of the feedback function, g(qo), in Bill’s PCT analysis? Well, of course one reason is mathematical; you can’t derive equation (1) above from the forward and feedback equations of PCT without equation (2) above. If you substitute qf for g(qo) you no longer see the inverse of the feedback function relationship between qo and qd; you have hidden the feedback function in qf.
RM: But another reason that it’s important to know that the behavioral illusion turns on the fact that system output, qo, affects the controlled variable, qi, is that the nature of the observed relationship between disturbance and output in a control system depends on the nature of the controlled variable itself. This is demonstrated in my “What is size” demo:
https://www.mindreadings.com/ControlDemo/Size.html
RM: In this demo, the observed relationship between disturbance, qd, and output, qo, depends on the variable being controlled. If the variable controlled is the perimeter of the rectangle then the relationship between qo and qd is qo = - qd; if the variable controlled is the area of the rectangle then the relationship between qo and qd is qo = qd^1/2. In both cases the feedback function relating qo to qi is the same: g() = 1.
RM: The different observed relationships between stimulus, qd,and response, qo, result from the difference in controlled variables. When perimeter is controlled the controlled variable is qi = qd + qo; when area is controlled the controlled variable is qi = qd * qo. In order to keep qi constant when perimeter is controlled qo must equal -qd and in order to keep qi constant when area is controlled qo must equal qd^1/2. Ergo the different relationships between qd and qo when different aspects of the environment – different controlled variables – are controlled.
RM: So the observed relationship between independent variable,qd, and dependent variable, qo – the supposed “organism” function – changes dramatically with nothing more than a change in the mind of the system doing the controlling about what aspect of the environment to control, perimeter or area.
RM: The fact that the observed relationship between qd and qo depends completely on the nature of the relationship between system output, qo, and the controlled variable, qi, doesn’t mean that there is no causal connection between qd and qo. Thinking that it did mean that is the mistake I made that Bill chided me for in the interaction between Bill and me that you posted. I had said:
RM: Yes, but is o really a causal function of d?
RM: And Bill explained that there certainly is:
BP: Yes .
RM: The fact that as late as 2012 I thought that the behavioral illusion meant that there was no causal connection between disturbance and system output shows that it is not that easy to understand PCT. In 2012 I had been working on PCT for over 30 years and I still didn’t fully understand some of the subtleties. All that the behavioral illusion shows is that the observed relationship between qd and qo – the relationship observed in virtually all psychological experiments – tells you nothing about the actual causal relationship between qd and qo.
RM: As Bill notes in his reply to me, the actual causal path from qd to qo goes from qd to qi to e to qo. Note that qi is in that path. So in order to understand the “forward” causal path through a control system from qd to qo you have to know qi – the controlled variable. So while I got it wrong about there not being a “forward” causal path from qd to qo in a control loop, I have always gotten right what is the most important lesson from the behavioral illusion, which is: in order to understand the behavior of a living control system you have to know what variables it is controlling – its controlled variables, qi.
AM: I have the impression that the behavioral illusion, as defined here, is not very common. I have found very few examples in the literature. Maybe I’m not looking to the right places.
RM: I think if you read on in the “behavioral illusion” section of the 1978 paper you will see that this illusion can be found in virtually every psychological experiment where it is reported that an independent variable was found to have an effect on a dependent variable. Here’s how Bill puts it:


RM: So the whole enchilada of understanding the behavior of living organisms hinges on knowing what variables organisms control. It’s all about controlled variables!
AM: Yeah, you’re preaching to the choir.
RM: Perhaps. But it looks to me like I am in the wrong church. I have not seen any evidence of research aimed at testing for controlled variables coming out of your lab. And your analysis of the behavioral illusion suggests that you don’t quite understand where controlled variables fit into the behavioral illusion.
AM: Psychologists have certainly mostly ignored controlled variables,
RM: “Totally ignored” would be a better way to put it.
AM: I’ve found a few examples where controlled variables are hypothesized, discussed and even tested for stability when disturbed, with reference to classical control theory. For example, the Center of Mass in maintaining balance literature, then various ‘muscle length’ , ‘muscle force’, ‘second derivative of force’, as measured by the muscle spindles and golgi tendon organs, etc. That is why I say mostly.
RM: I have found such examples as well. So how about “virtually totally ignored”.
Best regards
Rick