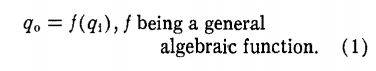Behavioral illusion, based on Powers (1978)

[amatic]

RM: But the actual forward functional relationship between qd and qo – the one described by equation (9) – is still in effect !
AM: No, this is not correct. The forward path is still in effect, but the functional relationships are changed because of feedback.
RM: I don’t see anything in the 1978 paper that suggests that this is the case.

You don’t see how the qd-qo function is changed because of feedback? You mean the abstract form of the function? Because the qd-qo plot surely changes.

RM: Behavioral Illusion

Cool, I have the same thing in simulation:

Google Colaboratory

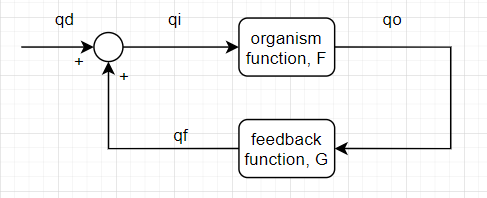
Here is the diagram that applies to the simulation and also to your experiment:

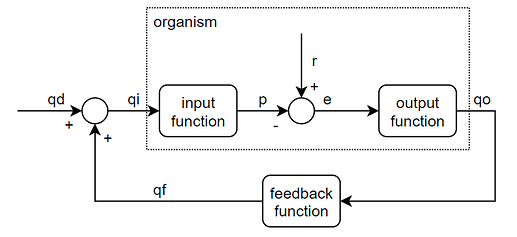
All the lines are signals, and all the circles and boxes are functions (not the same as Bill’s diagram in first post where lines are functions)

The feedback function is relating qo and qf.
A summing function is relating qi to qd and qf. That is the little circle on the left, sometimes called a summer, but often left nameless. A similar function in the middle relating e to r and p is usually called a comparator.
The feedback function is relating qf to qo, as in qf = G(qo)

This is also true in your code for the spider simulation:
https://www.mindreadings.com/ControlDemo/Illusion.js
in stepRun you have:
xpos = (-d[session][n]) + mx*1.5;

so to put it in terms of the diagram, qi = d + qo * Kf.
The feedback function is G is 1.5* x or qf = 1.5 * qo.

RM: According to you, the change in the qd-qo relationship with a change in the feedback function reflects an actual change in the forward path through the organism from qd to qo

No. According to me, closing the loop changes the functional relationship between qd and qo, it does not change the forward path. When the loop is closed, to quote myself:

AM: the forward path is still in effect, but the functional relationships are changed because of feedback.

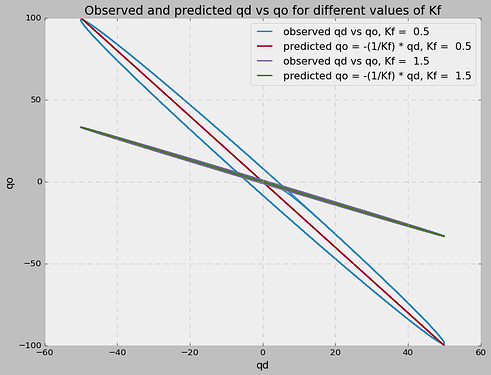
Changing the feedback function also changes the functional relationship between qd and qo, without any changes in the forward path, as demonstrated by both your and my demos. The only thing we changed was the Kf, and the functional relationship between qd and qo also changed.

What I mean when I say that the functional relationship between qd and qo has changed is that the two lines that represent two situations with strong and weak feedback have a different slope.
In the first case, qo = -2 * qd. In the second case qo = -0.66 * qd.

You seem to have a different understanding what “functional relationship” means when you say

RM: More compelling is the fact that these results can be precisely replicated by a model in which the functional relationship between qd and qo remains exactly the same when the feedback function changes from weak to strong.

In the abstract form, for ideal N system, it is always valid that qo = G^-1(qd). This abstract form does not change with changes in parameters.

I mean, I THINK my use of the idiom is correct. A functional relationship such as a = 2b is different from a = 3b, even though both are a = K*b.

AM: Your function 9 is only valid in an open loop, and does not “actually” exist in a closed loop, and it is certainly not in effect. causal path =/= functional relationship.

RM: Again, I don’t know what could possibly be your basis for saying this. I think there is no evidence at all that this is the case. Indeed, the only relevant evidence I know of is consistent with the idea that this is not the case.

The basis for saying that the equation

(9) qo = - ko*ki * d i

is only valid in the open loop is that when you solve the system of your equation 5-8 that represent an open loop system, you get the equation 9. When you solve equations 1-4, for the closed loop system, you get equation 10. Those equations are solutions for different systems, and the solution of 1-4 is not a valid solution for 5-8

RM: What you are saying is that the observed functional relationship g-1 between qd and qo for a closed loop system (top equation) *is now the actual system function, the equivalent of the function f [] for the same system if it were open loop. If this were the case then there would be no “illusion” involved when you look at the relationship between qd and qo for a closed-loop system. What you are seeing, according to you, is the organism function, which the closed-loop has changed from f to g-1 .

No, I’m just saying you are using the word “actual” too much.

What you call an “actual qd-qo relationship” is the open loop system function F, or maybe F (H(d)). . I’m saying that your use of that expression is nonsense. In a closed loop, the qd-qo relationship is different from the open loop qd-qo relationship. No need to add “actual” anywhere.

RM: . This is shown clearly by my model of the behavior in my “Behavioral Illusion” demo. The model shows that the change in the observed relationship between qd and qo with a change in the feedback function, g , occurs with no change at all in the ** actual function, f , relating qd to qo.** The illusion is that the the observed functional relationship between qd and qo in an N-Systems reflects characteristics of the organism when they actually reflect characteristics of the environment in which the organism is behaving

In a closed loop, F is relating qo to qi. The organism box in the diagram above is relating qo to qi. Also in Bill’s diagram copied in first post, the F function is relating qo to qi.

AM: In the behavioral illusion, there is no difference between “observed qd-qo” and “actual qd-qo”.
RM: I think that’s about as wrong as you can get. I don’t know how you are able to read the 1978 paper and not understand that the observed relationship between qd and qo not the same as the actual relationship between qd and qo; the former is the inverse of the feedback function, g-1, and the latter is the organism function, f.

I do know how. The latter (“actual qd-qo”) is not the organism function f . The organism function is relating qi and qo.

The “actual qd-qo” is just your term for open-loop function relating qd to qo, and is not the solution for the closed loop situation, and thus not at all relevant for the closed loop situation.

Why do you call the open loop qd-qo function the “actual qd-qo” function? Why would it be more actual than the closed loop function?

[amatic]

Is it not ironic that you call the F function the “actual qd-qo” function, and at the same time saying that it is an illusion to think that qd-qo is the F function?

[amatic]

RM: I’m sorry, I can’t just take your word for it. I have to see some evidence that this is the case before I can believe it.

Let’s say the organism function is:

Setting reference to 0, Ki =1, Kd = 1, and Ko = 100, we can have a simple organism function: F(x) = -100 * x, or inserting the variables:

(2) qo = -100 * qi

This is the “actual” organism function valid in open loop and in closed loop. It does not change when closing the loop.It is always relating qo to qi.

We can set the feedback function, relating qf to qo to a simple form G(x) = Kf * x, leaving Kf for now undetermined.

(3) qf = Kf * qo

and we have the summing function:

(4) qi = qd + qf

Assuming that the system is stable, we can find the general solution by shifting things around:

qo = -Ko * ( qd + qf)
qo = -Ko * ( qd + Kf *qo)
qo / -Ko = qd + Kf * qo
qo /-Ko - Kf * qo = qd
qo * (-1/Ko - Kf) = qd

(5) qo = qd / (-1/Ko - Kf)

If we set Kf to 0, we get the open loop solution:

qo = qd / (-1/100 - 0)
(6) qo = - 100 * qd

This means that if there is no feedback, qo will be 100 * amplified qd

If we set Kf to some other value, like 1, we get the closed loop solution:

qo = qd / (-1/100 - 1)
qo = qd / -1.01

(7) qo = -0.99 * qd

The solution (7) for the closed loop is not exactly the inverse of G, but it is pretty close, the qo will be very nearly -qd.

There was no change in the organism function F, relating qo to qi, There was only a change in G, relating qf to qo. This has resulted in two very different functions relating qo to qd.

open loop, Kf = 0:
(6) qo = - 100 * qd

closed loop, Kf = 1,
(7) qo = -0.99 * qd

The open loop function (6) is not valid in the closed loop, and the closed loop function (7) is not valid in the open loop.

Let’s try weak feedback, kf = 0.5, by inserting Ko and Kf into equation (5):
(5) qo = qd / (-1/Ko - Kf)

qo = qd / (1/100 - 0.5)

closed loop, Kf = 0.5
(8) qo = -1.96 * qd

This qo-qd relationship is nearly the inverse of the qf-qo relationship G. The exact inverse of G(x) = 0.5 * x would be G^-1(x) = 2 * x, but we get something very near, and we also have a change in sign of the inverse. The higher the Ko, the closer is qd-qo to the inverse of G.

This function (8) is not valid for the open loop, and it it is not valid for the closed loop when Kf = 1. It is only a valid solution for Kf = 0.5.

That is what I mean when I say that the functional relationship between qd and qo changes when you close the loop or when you change the feedback function. The organism function does not change, it is always relating qo to qi.

[rsmarken]

Hi Adam

RM: I’m sorry, I can’t just take your word for it. I have to see some evidence that this is the case before I can believe it.

AM: If we set Kf to 0, we get the open loop solution:

(6) qo = - 100 * qd

AM: If we set Kf to some other value, like 1, we get the closed loop solution:

(7) qo = -0.99 * qd

The solution (7) for the closed loop is not exactly the inverse of G, but it is pretty close, the qo will be very nearly -qd.

AM: That is what I mean when I say that the functional relationship between qd and qo changes when you close the loop or when you change the feedback function. The organism function does not change, it is always relating qo to qi.

RM: And that is exactly what Powers (and I) mean when we say that the observed functional relationship between qd and qo is different for Z and N systems with the same system (organism) functions. Equation (7) is the relationship between qd and qo that you observe when you are dealing with a closed loop system. The behavioral illusion is taking this relationship as that for an open loop system, the one defined by equation (6).

RM: I think the most informative way to proceed on this (for me anyway and, possibly, for anyone observing this conversation) would be for me to try to describe what I think Powers is saying in the 1978 paper and then for you to tell me how I am wrong. So here goes:

RM: Scientific psychology is based on the assumption that the behavior of organisms is ultimately caused by what happens to them. In terms of the notation used in the 1978 paper, psychologists assume that behavior, qo, is a causal function, f(), of stimulus input, qd. The goal of experimental research in psychology is, therefore, to find the causes of behavior, which means finding the qd that cause the qo.

RM: Psychologists try to achieve this goal by manipulating qd (independent variables) under controlled conditions to see if there is concomitant variation in qo (dependent variables). If qo is found to vary as a function, f(), of variation in qd then the conclusion is that qd causes qo. And f() is the characteristic of the organism that mediates this causal relationship: f() is the “organism function”.

RM: This is basic experimental psychology and it is the “foundation of scientific psychology” that is toppled by the “spadework” in Powers’ 1978 paper. The paper does this by showing that if the organism under study is a control system then the observed relationship between independent and dependent variable (qd and qo) is not a characteristic of the organism, f(), but, rather, is the inverse of the feedback connection, g(), from qo to the variable the organism is controlling – the controlled variable, qi. That is, in the typical psychology experiment what the researcher is seeing is g() -1 rather than f().

RM: The results of the conventional psychology experiment are, therefore, not what psychologists think they are. This is the behavioral illusion; taking the observed relationship between independent and dependent variable to reflect something about the organism when, in fact, it reflects something about the environment in which the organism does its controlling. This illusion does not happen because scientific psychologists are stupid or foolish. It happens because organisms are control systems and their behavior (controlling) looks like a cause effect process when researchers ignore or are unaware of the fact that variables are under control; that is, when they ignore or are unaware of controlled variables. And scientific psychologists have studiously ignored or simply remained unaware of the existence of controlled variables.

RM: In his 1978 Psych Review paper Powers showed that when you become aware of the existence of controlled variables the behavioral illusion disappears; you see that the relationship between qd and qo results, not from some causal relationship between them but, rather, from their mutual effect on a controlled variable via the closed negative feedback process of control; what you are seeing is the disturbance resisting characteristic of the behavior of a control system. Research aimed at finding relationships between independent and dependent variables (qd’s and qo’s) now becomes of little or no interest compared to research aimed at identifying controlled variables. That’s because once you know what variable is under control you know how the organism will respond (qo) to all possible disturbances to it (qds).

RM: The 1978 paper ends with a description of a method of identifying controlled variables called the test for the controlled variable. This is the model for behavioral research that is built on a new foundation; a foundation based on a control rather than a cause-effect model of behavior.

Best

Rick

[amatic]

RM:
Equation (7) is the relationship between qd and qo that you observe when you are dealing with a closed loop system. The behavioral illusion is taking this relationship as that for an open loop system, the one defined by equation (6).

I think I know what you mean and want you want to say, but it doesn’t sound quite right. You can perfectly observe equation 7 in some open loop system. And equation 6 does not define an open loop system. All three equations - 6, 7 and 8 are different solutions to a system of equations 1-5 for different values of Kf. Setting Kf to 0 is what defines this system as open loop.

Say we measure qd-qo relationship as qo = 5 * qd. There is no way to tell, just from the plot, if there is a closed loop here. We could be dealing with system a) or with system b):

a)
F(x) = 5 * x
G(x) = 0

b)
F(x) = 100 * x
G(x) = (1/5) * x

The behavioral illusion is thinking you have a) when you really have b). That’s how I’d go about defining it The only way to determine if it is a) or b) is to do more experiments.

We can try changing G to G(x) = 2 * x.
If we get qo = (1/2) * qd, it is b).
If we still get qo = 5 * qd, it is a).

It seems that in the rat example in the paper, the reinforcement rate was assumed to be this G function.

RM: I think the most informative way to proceed on this (for me anyway and, possibly, for anyone observing this conversation) would be for me to try to describe what I think Powers is saying in the 1978
[…]

The problem with the SR model is not that it is “causal”, but that this causality is lineal (in a chain, without feedback); and it is supposed to be “circular causality”, as in a system of equations with feedback. Maybe I’m too pedantic.

---

The reinforcement ratio example of the behavioral illusion in the paper is interesting as an example of PCT methods other than cursors and targets.

With some arbitrary values for parameters, I get a plot like this:

Google Colaboratory

This means that the simulated rat is maintaining his food intake (qi, eaten food) at the level of 10 pellets per hour. If the food is added to his plate at the rate qd, then his pressing rate will vary to still achieve the same food intake.

Another variable to test would be changes in Kf over time, this would be analogous to changes in the reinforcement ratio, something people seem to be doing in the liteature.

I can’t find the original paper from the rat example. I’m looking for more data in the reinforcement learning literature to try to see how to reinterpret the stimulus-response laws…

[rsmarken]

AM: Say we measure qd-qo relationship as qo = 5 * qd. There is no way to tell, just from the plot, if there is a closed loop here. We could be dealing with system a) or with system b):
a)
F(x) = 5 * x
G(x) = 0

b)
F(x) = 100 * x
G(x) = (1/5) * x

The behavioral illusion is thinking you have a) when you really have b). That’s how I’d go about defining it

RM: And that is exactly how I would define it (and have been defining it): The behavioral illusion is taking an observed relationship between qd and qo as the organism function for an open loop system when, in fact, it is the inverse of the feedback function for a closed loop system.

AM: The only way to determine if it is a) or b) is to do more experiments.

RM: Exactly. Which brings us back to my take on Powers’ 1978 paper which is the focus of this thread. I had asked you to tell me what you thought was wrong with the description of my take on that paper, as written in the previous post, because I think that that would help me understand why we seem to be in conflict about what that paper says when we seem to be in complete agreement about what the behavioral illusion is. I would appreciate it if you could do that for me now. I would be particularly interested in what you think of this segment of what I wrote:

RM: In his 1978 Psych Review paper Powers showed that when you become aware of the existence of controlled variables the behavioral illusion disappears; you see that the relationship between qd and qo results, not from some causal relationship between them but, rather, from their mutual effect on a controlled variable via the closed negative feedback process of control; what you are seeing is the disturbance resisting characteristic of the behavior of a control system. Research aimed at finding relationships between independent and dependent variables (qd’s and qo’s) now becomes of little or no interest compared to research aimed at identifying controlled variables. That’s because once you know what variable is under control you know how the organism will respond (qo) to all possible disturbances to it (qds).

Best

Rick

[amatic]

My main objection is that you seem to take the behavioral illusion as a fact evident from the assumptions of scientific psychology, something that everyone doing stimulus-response experiments is bound to commit. No need to prove it.

On the other hand, I think that behavioral illusion is just a hypothesis about someone’s system identification. It needs to be proven or demonstrated that a closed loop model with a particularly defined CV is a quantitatively better model than R=F(S), and that F, the SR law, is the inverse feedback function in the closed loop model.

“Scientific psychology” is a diverse field with many methods and models. Most of it is just looking for correlations between population level variables. “Result in Test A is a predictor for performance in task B in a young population”. “A phone poll on sample M predicts voting results for population N”. That is a huge swath of scientific psychology not affected by control theory nor the behavioral illusion.

We could look to areas where people are trying to do system identification, trying to find laws relating stimuli to responses trough organisms. When we find such a law in literature, I think we cannot say the law does not exists. It does, there really is a simple function relating S to R. You can predict R from S, with some error. In an analog computer for square roots, there is really a functional relationship between I and O, O ≊ sqrt( I ) ,( ≊ - nearly equal). Behavioral illusion only applies if the person assumes explicitly “the organism is sensing the stimulus and responding to it”, “things are happening open loop”.
That is just the first step. A lot of the time people are proposing not S-R, but some other model where the reaction was mediated by a third variable, they include something like feedback effects, or things that hint at controlled variables - motivational states, goals, reward-seeking, etc. In those cases, I think the behavioral illusion also does not apply, but it is quite possible that some feedback model would be quantitatively better than whatever the researcher used.

Now we need to do the experiments or study the literature to get raw data about individual performances, using some operational definition of the controlled variable. Then we fit model parameters to individual data, and make a quantitative comparison to see if the model is explaining the data better than other proposed models.

Is the feedback model better? Great, the S-R law in that research might be an example of the behavioral illusion. Also, we have a better explanatory model, reason enough to celebrate.

Is the S-R law reflecting the environment function? No? Maybe we could say it is a “version” of the behavioral illusion, Yes? That is textbook behavioral illusion.

---

The '78 paper shows that approach when analyzing the rat experiment. Also that other paper on applying a feedback model to rat behavior. Also the illusion of adaptation of motor system properties to load properties in LCVIII.

That is why l’m looking for raw data from reinforcement experiments.

[amatic]

RM: Powers showed that when you become aware of the existence of controlled variables the behavioral illusion disappears; you see that the relationship between qd and qo results, not from some causal relationship between them but, rather, from their mutual effect on a controlled variable.

Two objections - one small, on the use of ‘causal’. It is a very vague term. Maybe changes in the stimulus will always be followed by the change in the response, that does imply causality by some definitions. I think it is not exactly wrong to say “stimulus X causes response Y” in that situation, by that definition of causality.
It might be wrong to claim a lineal causal chain if there is a circular causal loop. It is not wrong to say there is a causal connection, but it is not very informative, and there are better ways to express the connection.

Second one, on “becoming aware of controlled variables”, related to “if you know how to look at behavior through control theory glasses, controlled variables are all over the place”. This sort of thinking could be very dangerous without strict verification of controlled variables. Sure, you can see hypothetical controlled variables all over the place. It is easy to fool yourself into thinking you understand a behavior just because you have a hypothesis on what is controlled.

[rsmarken]

Hi Adam

AM> My main objection is that you seem to take the behavioral illusion as a fact evident from the assumptions of scientific psychology, something that everyone doing stimulus-response experiments is bound to commit. No need to prove it.

RM: No, I take the behavioral illusion to be exactly what Powers says it is in the Psych Review paper: The illusion is a fact if living systems are N - Systems (negative feedback control systems). And I think there is pretty overwhelming evidence that they are.

AM: On the other hand, I think that behavioral illusion is just a hypothesis about someone’s system identification.

RM: That’s not quite the way it is viewed in the 1978 paper. It is based on the hypothesis that organisms are N-Systems. But there is nothing in Powers’ paper that says it occurs because of someone’s system identification (I presume you mean as a Z , P or N-System – the three general types of system described in Powers’ paper). It occurs only if the system under study is an N-System and variations in disturbances to a controlled variable are seen as the cause of system outputs. There is a whole sub-field of psychology which I call “manual control theory” that identifies organisms as N- Systems and still sees disturbances as the cause of output. How one identifies the system under study has nothing to do with whether or not they are seeing a behavioral illusion

AM: It needs to be proven or demonstrated that a closed loop model with a particularly defined CV is a quantitatively better model than R=F(S), and that F, the SR law, is the inverse feedback function in the closed loop model.

RM: That has been “proven” many times over. It’s easy to “prove” using the methodology Powers described in that paper: by applying the test for the controlled variable.

AM: “Scientific psychology” is a diverse field with many methods and models.

RM: And because it’s a diverse field there are many different ways to experience the behavioral illusion. I describe three ways in my “Blind men and the Elephant” paper in MORE MIND READINGS.

AM: We could look to areas where people are trying to do system identification, trying to find laws relating stimuli to responses trough organisms. When we find such a law in literature, I think we cannot say the law does not exists.

RM: Sure, the observed relationship between qd and qo for a particular controlled variable will be quite lawful if the feedback function is the same each time the relationship is observed.

AM: Behavioral illusion only applies if the person assumes explicitly “the organism is sensing the stimulus and responding to it”, “things are happening open loop”.

RM: That is not how the behavioral illusion is described in Powers’ paper. The behavioral illusion Powers described in the 1978 paper is happening if the observed function relating qd to qo for a living system – an N - System-- is assumed to reveal something about the nature of the system itself when it doesn’t. That’s the “nightmare” Powers mentions at the end of the section on the behavioral illusion.

AM: Now we need to do the experiments or study the literature to get raw data about individual performances, using some operational definition of the controlled variable. Then we fit model parameters to individual data, and make a quantitative comparison to see if the model is explaining the data better than other proposed models.

RM: Yes, that would be a great idea. I’ve been doing that kind of research for over 30 years. It would be nice to have you join me.

Best

Rick

[rsmarken]

RM: Powers showed that when you become aware of the existence of controlled variables the behavioral illusion disappears; you see that the relationship between qd and qo results, not from some causal relationship between them but, rather, from their mutual effect on a controlled variable.

AM: Two objections - one small, on the use of ‘causal’. It is a very vague term.

RM: It’s interesting that you didn’t seem to think it was particularly vague when you posted Bill’s correction to my idea that there was no causal connection from qd to qo. In his answer tome Bill said:

BP: There is clearly a causal path from d to qi (the disturbance function), another from qi to e (perceptual function and comparator with an input from r), another from e to o (output function), and finally another from o to qi (environmental feedback function). All but the last work in the “forward” direction.

AM: It might be wrong to claim a lineal causal chain if there is a circular causal loop.

RM: That’s exactly what I thought and thaty exactly what Bill was correcting me on.

AM: It is not wrong to say there is a causal connection, but it is not very informative, and there are better ways to express the connection.

RM: So Bill could have just expressed it better? I’d like to know the better way to express what Bill said above. Maybe “There is not clearly a causal path …”

AM: Second one, on “becoming aware of controlled variables”, related to “if you know how to look at behavior through control theory glasses, controlled variables are all over the place”. This sort of thinking could be very dangerous without strict verification of controlled variables.

RM: The idea that there are controlled variables all over the place is dangerous? No wonder you guys avoid talking about them. I thought that understanding the ubiquity of controlled variables was the very basis for the existence of PCT. If you are not aware of the ubiquity of controlled variables then why in the world are you interested in PCT? PCT was developed to explain the existence of controlled variables. I guess the idea that controlled variables are all over the place is dangerous if – like virtually all behavioral scientists – one’s career is based on the idea that they don’t exist. But they don’t scare me. I kind of like them. And they played a very prominent role in Bill’s 1978 paper.

AM: Sure, you can see hypothetical controlled variables all over the place.

RM: There you go! That’s how PCT-based research starts!

AM: It is easy to fool yourself into thinking you understand a behavior just because you have a hypothesis on what is controlled.

RM: Yes, people fool themselves this way all the time. They do it when they try to understand what a person is doing by guessing what he or she is “up to”; what their purpose is. What these people are doing is guessing (forming hypotheses about) what variable(s) the person is controlling. These guesses are typically wrong. But people who understand PCT know that they must test their guesses about the variables a person (or other organism) is controlling. The method of doing this is called the test for the controlled variable, which, as I mentioned, is presented as the denouement to Powers critique of scientific psychology.

Best

Rick

[amatic]

AM: My main objection is that you seem to take the behavioral illusion as a fact evident from the assumptions of scientific psychology, something that everyone doing stimulus-response experiments is bound to commit. No need to prove it.

RM: No, I take the behavioral illusion to be exactly what Powers says it is in the Psych Review paper: The illusion is a fact if living systems are N - Systems (negative feedback control systems). And I think there is pretty overwhelming evidence that they are.

You say “no”, but then you say it is a fact. Let me try again - you would say that anyone doing stimulus-response experiments on living organisms is necessarily under the behavioral illusion, because (or if) they take the stimulus-response laws to reflect something about the organism?

In other words, there is no need to show that any particular stimulus-response law is better explained as a relationship between some variables in a closed loop?

It is self evident from their assumption of lineal causal chain, and our assumption of causal loop,that they are under the behavioral illusion, and we are right?

RM: There is a whole sub-field of psychology which I call “manual control theory” that identifies organisms as N- Systems and still sees disturbances as the cause of output. How one identifies the system under study has nothing to do with whether or not they are seeing a behavioral illusion

Wait, so are they are seeing the behavioral illusion or they are not?

[amatic]

RM: It’s interesting that you didn’t seem to think it was particularly vague when you posted Bill’s correction to my idea that there was no causal connection from qd to qo.
RM: So Bill could have just expressed it better? I’d like to know the better way to express what Bill said above. Maybe “There is not clearly a causal path …

Yeah, and he usually did. A better way to describe relationships between variables in behavior is to use functions, not listing causal connections. If someone says that stimuli cause responses, that is not an error if it means something like “stimulus precedes response”. Listing causes is simply not as informative as building a functional description.

[amatic]

AM: Behavioral illusion only applies if the person assumes explicitly “the organism is sensing the stimulus and responding to it”, “things are happening open loop”.

RM: That is not how the behavioral illusion is described in Powers’ paper. The behavioral illusion Powers described in the 1978 paper is happening if the observed function relating qd to qo for a living system – an N - System-- is assumed to reveal something about the nature of the system itself when it doesn’t. That’s the “nightmare” Powers mentions at the end of the section on the behavioral illusion.

bold - Sure it is. That is what a zero-feedback system means - the organism is sensing the stimulus - there are no controlled variables acting in between, things are happening open loop.

Where is the disagreement?

The person will assume that the qd-qo function reveals something about the nature of the system (the organism function) IF they also assume that the organism is sensing the stimulus and responding to it open loop.

Premises:
there is a function O transforming S to R, between a stimulus and a behavioral response.
It is found that O is R = log(S)

Therefore:
The organism is doing the function log(S).
We should look for that log function somewhere in the brain. It is transforming the stimulus to the response according to a log function. Maybe it is this part of the brain right here (pokes parts of the brain connecting sensory nerves to the brain area).

---

There is a possible behavioral illusion. The nightmare would be if there was really a controlled variable between S and R, and the log function was an artifact of our experimental setup, and not a function ‘implemented’ between the stimulus and the response in the organism.

[rsmarken]

Hi Adam

AM: My main objection is that you seem to take the behavioral illusion as a fact evident from the assumptions of scientific psychology, something that everyone doing stimulus-response experiments is bound to commit. No need to prove it.

RM: No, I take the behavioral illusion to be exactly what Powers says it is in the Psych Review paper: The illusion is a fact if living systems are N - Systems (negative feedback control systems). And I think there is pretty overwhelming evidence that they are.

AM: You say “no”, but then you say it is a fact.

RM: The “no” was to your suggestion that I take the behavioral illusion as a fact evident from the assumptions of scientific psychology. Actually, I take it as a fact that is evident from the difference between the behavior of a closed and open loop system. The behavioral illusion described in Powers’ 1978 paper is seeing the relationship between qd and qo as reflecting f(), the organism function, when in fact it reflects g()-1, the inverse of the feedback function. That fact is equivalent to the fact that you will see a straight stick as bent when it is placed in water; the bend you see is not the actual shape of the stick.

RM: And by the way, like the bent stick illusion, the behavioral illusion doesn’t go away once you know why the illusion happens. The stick appears bent even if you know that the bending results from the differential refraction of light by air and water. Similarly, the observed relationship between qd and qo appears to be mediated by the organism – the organism appears to be reacting, qo, to the the stimulus, qd – even if you know that this relationship is really the inverse of the feedback relationship between qo and qi. For example, I can see the behavioral illusion by looking at the pupillary reflex. It looks to me like shining a light in the eye, qd, causes the pupil to contract, qo, even though I know that what I am seeing is the inverse of the feedback connection between qo and qi, the connection between pupil size, qo, and the amount of light falling on the retina, qi, the controlled variable.

AM: Let me try again - you would say that anyone doing stimulus-response experiments on living organisms is necessarily under the behavioral illusion, because (or if) they take the stimulus-response laws to reflect something about the organism?

RM: Yes, if the observed S-R relationship is the qd - qo relationship seen in the behavior of a control system controlling a variable, qi, that is simultaneously affected by qd and qo. That is, if the system under study is an N System controlling qi.

AM: In other words, there is no need to show that any particular stimulus-response law is better explained as a relationship between some variables in a closed loop?

RM: Yes, there is no need to show that any particular stimulus-response law is better explained as a relationship between some variables in a closed loop. That is the basic conclusion of Bill’s 1978 paper. As Bill said in the Foreword to my book MIND READINGS (1992) “if the phenomenon you see here really works as this model shows it to work, then a whole segment of the scientific literature needs to be deposited in the wastebasket”. He was talking, of course, about the literature of scientific psychology. The phenomenon he was talking about is control and the model is, of course, PCT. The research and modeling described in MIND READINGS, which implements the tests described in the 1978 paper, shows that the focus of the study of living control systems should be on determining the variables they control, not on the relationship between disturbances and output.

RM: It might seem like it would be nice to show how all the stimulus-response relationships found in conventional psychology can be better explained by a closed loop model. But there are many things about conventional psychological research that suggest that this would be a colossal waste of time (hence the wastebasket). In order to create a closed loop model of an S-R relationship you first have to come up with a hypothesis about the variable being disturbed by S and controlled by R --the controlled variable. That shouldn’t be hard as long as it’s clear that S is truly an independent variable (qd) and R is truly a dependent variable (qo). But in many experiments S is an independent variable in name only (it is not a variable that is varied independently by the experimenter, such as gender). And R may be directly dependent on S so that there is no “room” for a controlled variable between them. In these cases you don’t have a situation where there might be a controlled variable that is being disturbed by S and this disturbance is being compensated for by R.

RM: But assuming you can find good old conventional research where S is really an IV and R is really a DV you still have the problem that most of the results of this research are very noisy and are presented as averages over many subjects. The noisy results could result from individual differences in the variables being controlled, the skill of controlling the variables or just difference in the S-R transfer function across subjects. And the averaging can produce results that are very misleading (See Powers, 1990, American Behavioral Scientist, v. 34). So, again, I think it’s best to do what Bill had always suggested by done -and certainly what he strongly implied i the 1978 Paper is what should be done – which is to just start psychological research all over again based on an understanding of organisms as purposive systems, controlling their perceptual inputs. The aim of such research would be to find what perceptual inputs – what controlled variables – organisms control.

RM: There are the occasional studies that lend themselves to a closed loop analysis. The studies of object interception that I analyzed are an example. And your studies of movement production are another. But in general I think trying to analyze existing research from a PCT perspective is pretty much a fool’s errand. I believe that this is the bottom line conclusion of Bill’s 1978 paper. The revolution in psychology Bill was describing was largely a methodological revolution. The study of living control systems – the purposive systems whose behavior was quantitatively analyzed in the 1978 paper – has to be aimed at determining the variables these systems control and how they control them. This can’t be achieved using the standard methods of psychological science – methods borrowed from the physical sciences where the systems under study have no purposes; they don’t control. That’s why the 1978 paper ends with a description of the test for the controlled variable. In order to understand the behavior of purposive (control) systems you have to know their purposes (the variables they control) and you can’t find that out using the conventional methods of the psychological (and physical) sciences. Those methods produce misleading results (such as the S-R behavioral illusion).

AM: It is self evident from their assumption of lineal causal chain, and our assumption of causal loop,that they are under the behavioral illusion, and we are right?

RM: Assumptions have nothing to do with it. As I said above, you are seeing the behavioral illusion whenever you see qd as the cause of qo when, in fact, what you are seeing is the inverse relationship between qo and qi for a control system. As with the bent stick in water, knowing why you are seeing it this way doesn’t prevent you from seeing it that way. The question, though, is whether what you are seeing is, indeed, an illusion; the stick may really be bent, qd may really be the cause of qo. The way to test whether qd is, indeed, the cause of qo is by using (all together now) the test for the controlled variable. If qd is not a disturbance to a controlled variable there is no variable being controlled then there was no illusion; qd is the cause of qo.

RM: There is a whole sub-field of psychology which I call “manual control theory” that identifies organisms as N- Systems and still sees disturbances as the cause of output. How one identifies the system under study has nothing to do with whether or not they are seeing a behavioral illusion

AM: Wait, so are they are seeing the behavioral illusion or they are not?

RM: Yes they are. Very much so. It’s the input-output blunder described in the 1978 paper.

Best

Rick

[rsmarken]

Hi Adam

RM: It’s interesting that you didn’t seem to think it was particularly vague when you posted Bill’s correction to my idea that there was no causal connection from qd to qo.
RM: So Bill could have just expressed it better? I’d like to know the better way to express what Bill said above. Maybe “There is not clearly a causal path …

AM: Yeah, and he usually did. A better way to describe relationships between variables in behavior is to use functions, not listing causal connections. If someone says that stimuli cause responses, that is not an error if it means something like “stimulus precedes response”. Listing causes is simply not as informative as building a functional description.

RM: In this case I think it’s important to distinguish causal functions from non-causal functions. I had asked Bill if qo was really a causal function of qd (I called them o and d). His answer was an emphatic Yes. He went on to say:

BP: There is clearly a causal path from d to qi (the disturbance function), another from qi to e (perceptual function and comparator with an input from r), another from e to o (output function), and finally another from o to qi (environmental feedback function). All but the last work in the “forward” direction.

RM: Note that Bill says that there is a causal path from d to qi but he did not say that there is a causal path from from qi to d. That’s because there isn’t. The functional relationship between d and qi is one way: d causes qi; but qi does not cause d. This is important because it means that, while the “forward” function relating d to o, o = f(d), in a control loop is causal, the inverse of the feedback function relating d to o, o = g-1(d), that we see in the behavioral illusion, is NOT.

RM: The forward causal path in a control loop – the forward function relating d to o – goes like this: d causes qi causes e causes o. The inverse of the feedback function relating d to o – the function that we see in the behavioral illusion – goes like this: o causes qi which DOES NOT cause d. So the forward path in a control loop is a causal function relating d to o; the feedback function in a control loop is is not causal because there is no causal connection between the variables that make up one one component of that function – the component relating qi to d.

RM: What this means, of course, is that even if you know that the observed functional relationship between d and o is the inverse of the feedback function relating o to qi, you can’t use this knowledge to recover the “forward” function from d to o. If the system under study is an N System – which is something you can determine by doing the test for the controlled variable – then the only way to learn about its actual “forward” function is by learning what variable(s) it is controlling.

Best

Rick

[amatic]

Thanks for the thoughtful post. I agree with a lot of it. Here are some questions.

Let’s say there is a study, one of those “wastebasket” ones, where the S-R relationship is just barely fitted to a linear function, the prediction of response from stimulus can be made only with a large error.

I think they are not seeing the inverse of the feedback function here, they are just seeing some randomness coming from, as you say, individual differences in performance, controlled variables, reference levels, etc. They could be seeing an artifact like the one in Control Theory and Statistical Generalizations (Powers, 1990)

So, my question is, if they are not seeing the inverse of the feedback function, but some statistical artifact, is this a behavioral illusion or not?

RM: The behavioral illusion described in Powers’ 1978 paper is seeing the relationship between qd and qo as reflecting f(), the organism function, when in fact it reflects g()-1, the inverse of the feedback function.
RM: As I said above, you are seeing the behavioral illusion whenever you see qd as the cause of qo when, in fact, what you are seeing is the inverse relationship between qo and qi for a control system.

The researchers probably are taking the stimulus to be the cause of the response, but they are seeing a statistical artifact quite a bit different than the inverse of the environment function. Even if the environment is the same for all subjects in a study, they might be controlling different variables, so the G function might be different for different subjects, and add different aspects of behavior to qi, and the H function would add different aspects of the stimulus to qi.

They probably think that the S-R relationship found in that research is revealing something about the organism function F(), but it might just be a statistical artifact, not the inverse of G, but an artifact coming from individual differences and the method of generalizations. I would not call this artifact “the behavioral illusion”, it is a different phenomenon.

Similarly:

AM: [are engineering psychologists seeing the behavioral illusion?]
RM: Yes they are. Very much so. It’s the input-output blunder described in the 1978 paper.

You mean “the input blunder”. I don’t see any evidence that the engineering psychologists are mistaking the closed loop function for the open-loop, or even that they have causal relationships somehow wrongly attributed. They are using control theory methods, just like Bill did, the math is pretty much the same. The blunder is just in putting the reference signal outside the subject.

BP (1978, p 421): I hope my implied criticisms have stayed on target because there is no reason to belittle what cyberneticists have done or what engineering psychologists have discovered.

It is an important blunder with some consequences on building a hierarchy and interpreting purposes in subjects, etc, etc, but it is not the behavioral illusion, and the findings of engineering psychologists probably are revealing much about the subjects they study. They study individuals, they build models, etc.

RM: In this case I think it’s important to distinguish causal functions from non-causal functions. I had asked Bill if qo was really a causal function of qd (I called them o and d). His answer was an emphatic Yes . He went on to say:

Yeah, I think he was answering your “am I wrong?” question with “yes”. I don’t see anyone talking about “causal functions” anywhere. You might have invented the term. But lets see the proposal…

o = f(d) : causal function
o = g^-1(d) : not causal function

d => qi => e => o => qi // forward causal path
o => qi NOT=> d // inverse of the feedback function

---

I mean, the feedback path is causal in relating qo to a part of qi. Where is that causal function? A nicer way (at least to me) of explaining why we have the inverse is by using the “backwards reasoning”.

---

If we know F is a high gain amplifier, we know qi is going to be zero (for r=0). Going backwards (left), the sum of qd and qf is zero only if they are equal, but opposite sign, so qf = -qd. Reading the diagram, ee know qf = G(qo). So, we also know that qo = G^-1 (qf).
Because qf is equal to -qd, we now get qo = - G^-1(qd)

This analysis assumes an ideal amplifier as F, with infinite gain. In reality, qi will not be zero, and qd will not be equal to -qf, but very near, and that is why we don’t get the exact inverse, but a value near it. Since organisms are generally not ideal control systems, the qo will not be exactly the inverse of G of qd, but something near it, depending on the gain.

[rsmarken]

Hi Adam

AM: Let’s say there is a study, one of those “wastebasket” ones, where the S-R relationship is just barely fitted to a linear function, the prediction of response from stimulus can be made only with a large error.

RM: I’d say that’s the typical result of psychological research. Several years ago I did a little survey of research appearing in Psychological Science, one of the premier scientific psychology journals. I found that the average Eta^2 (equivalent to R^2) value for the results of about 100 studies was .32. Given that extremely low proportion of variance in R (the DV) that is typically accounted for by S (the IV) it’s no wonder that the replication rate for such studies is dismally low.

AM: I think they are not seeing the inverse of the feedback function here, they are just seeing some randomness coming from, as you say, individual differences in performance, controlled variables, reference levels, etc.

RM: I agree.

AM: They could be seeing an artifact like the one in Control Theory and Statistical Generalizations (Powers, 1990)

RM: Yes. Although that is a correlational relationship since the measures of both reward and effort are produced by the subjects themselves. I think Bill presented this as a worst case scenario to show what could happen when you average over subjects and those subjects happen to be control systems. There are surely other interesting ways that averaging over subjects can screw things up. Averaging over subjects would only be ok if subjects really behave according to the general linear model, which is, of course, the basis of all statistical analysis in psychology.

RM: According to the general linear model the behavior of all subjects in an experiment can be approximated as: R.i = a + b.i*S + e.i, where a is the average effect of S on R for all subjects, b.i is the difference between the average effect of S and the specific effect of S for subject i and e.i is a random error added to the R for subject i. Conventional psychologists would say that the observed relationship between S and R in their experiments results from e.i being so large. In his wonderful book “People as Living Things” (2003) Phil Runkel explained why this idea is rather ridiculous (p. 167). If you don’t have a copy, get one; it’s one of the best books on PCT that’s out there.

AM: So, my question is, if they are not seeing the inverse of the feedback function, but some statistical artifact, is this a behavioral illusion or not?

RM: I suppose it could be called a behavioral illusion. If researchers see their results as being produced by an S-R system of the form R.i = a + b.i*S + e.i when those results are actually being produced by control systems, then they are seeing a version of the S-R behavioral illusion described in Bill’s 1978 paper. But I think we can get carried away with trying to determine whether any particular research result is really a behavioral illusion. I think the main point of the 1978 paper is this: research that ignores the possible existence of controlled variables – research that ignores the possibility that the system under study may be an input control system – is likely to produce misleading results.

RM:: The S-R illusion that Bill describes in the 1978 paper is only one possibility. Another illusion is that reinforcements selects behavior; this illusion ignores the fact that the organism is controlling something about the reinforcement, such as its rate or probability. (Actually Bill did allude to this illusion in the 1978 paper when he says: "Skinner’s discovery is better stated in the following way: Behavior exists only to control consequences that affect the organism). And still another is the illusion that behavior is emitted output; in this case the behavior itself is likely to be a controlled variable that is being protected from invisible disturbances (like the forces acting on your movements when you lift a cup of tea to your lips) by invisible actions (the muscle forces that counter these disturbances while you lift the cup to your lips).

RM: Bill described only the S-R illusion in the 1978 paper because he was focusing on the problem that results when IV-DV methodology – the basic method of scientific psychology – is used when studying living control systems. But the more general message of that paper was that this illusion results from ignoring controlled variables. So research aimed at understanding the behavior of living systems should start with identification of the controlled variable(s), qi, around which the behavior is organized. This is done using some version of the test for the controlled variable. If the test reveals that there is no controlled variable involved in the behavior (an extremely unlikely discovery when the subjects of study are living control systems) then there is no control involved in the behavior and the research can be handed over to physicists.

RM: The behavioral illusion described in Powers’ 1978 paper is seeing the relationship between qd and qo as reflecting f(), the organism function, when in fact it reflects g()-1, the inverse of the feedback function.
RM: As I said above, you are seeing the behavioral illusion whenever you see qd as the cause of qo when, in fact, what you are seeing is the inverse relationship between qo and qi for a control system.

AM: The researchers probably are taking the stimulus to be the cause of the response, but they are seeing a statistical artifact quite a bit different than the inverse of the environment function. Even if the environment is the same for all subjects in a study, they might be controlling different variables, so the G function might be different for different subjects, and add different aspects of behavior to qi, and the H function would add different aspects of the stimulus to qi.

AM: They probably think that the S-R relationship found in that research is revealing something about the organism function F(), but it might just be a statistical artifact, not the inverse of G, but an artifact coming from individual differences and the method of generalizations. I would not call this artifact “the behavioral illusion”, it is a different phenomenon.

RM: But if the system under study is a control system and S is truly an independent variable and the observed R is not something that would be expected based on physics then it’s likely that R is an action (or related to an action) that is aimed at keeping a controlled variable under control. I’m sorry to keep harping on controlled variables so much but they are really the central phenomenon to be explained by PCT; they are the phenomenon that is ignored or denied by conventional scientific psychologists, to the considerable detriment of scientific psychology according to the 1978 paper. Any research on living organisms that is not based on explaining the existence of controlled variables and how the organism controls them is missing what is most important about the behavior of living organisms and, at the same time, misleading themselves with observations that could be called illusions.

AM: [are engineering psychologists seeing the behavioral illusion?]
RM: Yes they are. Very much so. It’s the input-output blunder described in the 1978 paper.

AM You mean “the input blunder”.

RM: Yes.

AM: I don’t see any evidence that the engineering psychologists are mistaking the closed loop function for the open-loop, or even that they have causal relationships somehow wrongly attributed. They are using control theory methods, just like Bill did, the math is pretty much the same. The blunder is just in putting the reference signal outside the subject.

RM: Leave out the “just” and I agree. Unfortunately, they also leave out the perceptual function which, in living systems, means leaving out the function around which its behavior is organized. So the research of manual control theorts, like that of other conventional psychologists, completely ignores the variable around which the behavior of the system is organized – the controlled variable.

AM: quoting Powers: BP (1978, p 421): I hope my implied criticisms have stayed on target because there is no reason to belittle what cyberneticists have done or what engineering psychologists have discovered.

AM: It is an important blunder with some consequences on building a hierarchy and interpreting purposes in subjects, etc, etc, but it is not the behavioral illusion, and the findings of engineering psychologists probably are revealing much about the subjects they study. They study individuals, they build models, etc.

RM: I’ll answer by also quoting Bill:

BP (1978, p. 420) If one’s primary purpose is to keep pilots from flying airplanes into the ground or to make sure that a gunner hits a target with the shell, that is, if one’s purposes concern objectivized side effects of control behavior, the man-machine blunder amounts to nothing worse than a few mislabelings having no practical consequences. If one’s interest is in the properties of persons, however, the man-machine blunder pulls a red herring across the path of progress.

RM: A red herring is, of course, a diversion – a compelling observation that attracts one’s attention away from what’s really going on. Engineering psychologists have found out interesting things about the dynamics of human control when they know what variables the human is supposed to control. They can then evaluate human performance by comparing it to that of models controlling those variables. But that doesn’t tell you much about behavior when you don’t know what the system itself is trying to accomplish.

AM: I mean, the feedback path is causal in relating qo to a part of qi. Where is that causal function?

RM: In a tracking task qi = m + d. So the state of the controlled variable is simultaneously caused my mouse movement, m, and the disturbance variable, d. So qi is a causal function of both output (m) and disturbance (d).

AM: A nicer way (at least to me) of explaining why we have the inverse is by using the “backwards reasoning”.

RM: That’s fine. You get the same result as we do so if your way works for you then that’s great.

Best

Rick

[amatic]

It is quite strange talking to you.

RM: The S-R illusion that Bill describes in the 1978 paper is only one possibility.

Yeah, that is really the point from the start of the topic. The behavioral illusion is a very specific phenomenon. Each of the examples in the paper contain a misidentification of a closed loop system as an open loop system and attribution of the environment function to the organism function. Of course, there are many other possible illusions, mistakes, artifacts, etc.

RM: In a tracking task qi = m + d. So the state of the controlled variable is simultaneously caused my mouse movement, m, and the disturbance variable, d. So qi is a causal function of both output (m) and disturbance (d).
RM: That’s fine. You get the same result as we do so if your way works for you then that’s great.

You’re sticking with that? Interesting. Maybe I missed a day in school, teach me more. What are causal functions? How exactly do you define them? (I can’t find anything relevant on google, just some niche engineering uses of the term)?

What is the difference between causal and non-causal functions? How are causal functions different from just regular functions?

Most importantly, how do they get you the same result as the “reasoning backwards” technique when it comes to the behavioral illusion, or when it comes to getting the inverse of the feedback function? What is the causal calculus? Or is it causal arithmetic?

[rsmarken]

Hi Adam

RM: In a tracking task qi = m + d. So the state of the controlled variable is simultaneously caused my mouse movement, m, and the disturbance variable, d. So qi is a causal function of both output (m) and disturbance (d).
RM: That’s fine. You get the same result as we do so if your way works for you then that’s great.

AM: You’re sticking with that? Interesting. Maybe I missed a day in school, teach me more. What are causal functions? How exactly do you define them? (I can’t find anything relevant on google, just some niche engineering uses of the term)?

AM: What is the difference between causal and non-causal functions? How are causal functions different from just regular functions?

RM: I use the term “causal function” to refer to a mathematical description of the causal relationship between two variables. A “non-causal” function is, then, a mathematical description of the relationship between two variables that are not causally related. The difference is equivalent to that between correlation and causality. Correlation is a functional (mathematical) relationship between variables. When there is a correlation between variables the actual relationship between them may be causal (such as the relationship between voltage and current; voltage causes current) or not (such as the relationship between the time of day and the outdoor temperature).

RM: I base the distinction I make between causal and non-causal functions on Bill’s reply to my question “but is o really a causal function of d”? Bill replied:

BP: Yes . There is clearly a causal path from d to qi (the disturbance function), another from qi to e (perceptual function and comparator with an input from r), another from e to o (output function), and finally another from o to qi (environmental feedback function). All but the last work in the “forward” direction.

RM: That “Yes” suggests that Bill understood what I meant by “causal function” and he proceeded to describe the causal functions in a feedback loop: the disturbance function, qi = h(d), the perceptual function, p = I (s.1, s2…s.n), the comparator function, e = r - p, the output function, o = O (e) and the feedback function, qi= g(o). These are all “causal functions” in the sense that they are mathematical descriptions of the causal path between variables. The forward path causal functions – qd to qi to p to e to qo – can be written as a single “organism function”, F() so that qo = F(qd). The feedback function, qi = g(qo) is the only “backward” function. So there is a two way causal path between qi and qo – a forward path from qi to qo through the organism and a backward path from qo to qi through the environment.

RM: The function Bill didn’t mention as a causal function was the one relating qi back to d – the inverse of the disturbance function: d = h-1(qi). That’s because the causal path between d and qi is one way – forward from d to qi but not backward from qi to d. So the inverse of the disturbance function, d = h-1(d), is non-causal function because there is no causal path from qi to d.

RM: Scientific psychologists consider the path from qd (the IV) to qo (the DV) to be causal. Thus, when they find a mathematical relationship between qd and qo in an experiment they assume that it is an approximation to F(), the organism function, which is a description of the causal path that relates IV to DV via the organism. Bill’s paper shows that, if the organism under study is a closed loop system, then the observed relationship between qd and qo (IV and DV) is actually a mathematical approximation to the inverse of the feedback function that relates the DV (qo) to the controlled variable, qi (not to the IV, qd).

RM: The point of Bill’s answer to my question about whether there is really a causal connection between qd and qo was that even if the organism under study is a control system there is still a forward causal path from IV (qd) to DV (qo) through the organism. His answer made me realize that what I was missing is that there is no a backward causal path from qo to qd because there is no causal path from qi to d. So another way to look at the behavioral illusion is that a “non causal” function – the inverse feedback function relating qo to qd – is seen as a “causal” function – the organism function that characterizes the causal path from qd to qo.

AM: Most importantly, how do they get you the same result as the “reasoning backwards” technique when it comes to the behavioral illusion, or when it comes to getting the inverse of the feedback function? What is the causal calculus? Or is it causal arithmetic?

RM: I tried to describe it above. I hope that’s clear. Maybe I should add that you can only recover the forward causal function from the observed inverse feedback function if you know qi. That’s because the feedback function relates qo to qi, not qo to qd. So what you are observing as the relationship between qo and qd is actually the inverse of the relationship between qo and qi. Once you know qi you can put all the variables into a model to see kind of system that produces the observed relationship between qd and qo.

Best

Rick

[amatic]

RM: I base the distinction I make between causal and non-causal functions on Bill’s reply to my question “but is o really a causal function of d”? Bill replied:

Notice that he uses the term “causal path”, not “causal function”, and generally never used “causal function”.

RM: and the feedback function, qi= g(o).
RM: The feedback function, qi = g(qo) is the only “backward” function
is actually a mathematical approximation to the inverse of the feedback function that relates the DV (qo) to the controlled variable, qi (not to the IV, qd).

There is a causal path, or causal link, causal something, from qo to qi, passing trough the environment, through the feedback function. The environment is usually modeled with two functions, one is G, and the other is the adding of G(qo) and H(d), or qd and qf (or whatever you want to name it), to finally make qi. Well, H is a third environmental function. What you wrote (four, five times) is not the feedback function as defined in PCT.

RM: So what you are observing as the relationship between qo and qd is actually the inverse of the relationship between qo and qi.

It looks to me like your causal analysis led to you to a mistaken conclusion. As I’m sure you know from the test for the controlled variable, the relationship between qi and qo in a good control system should be a low, near zero correlation. If there is no correlation, you can’t describe the relationship as a function.