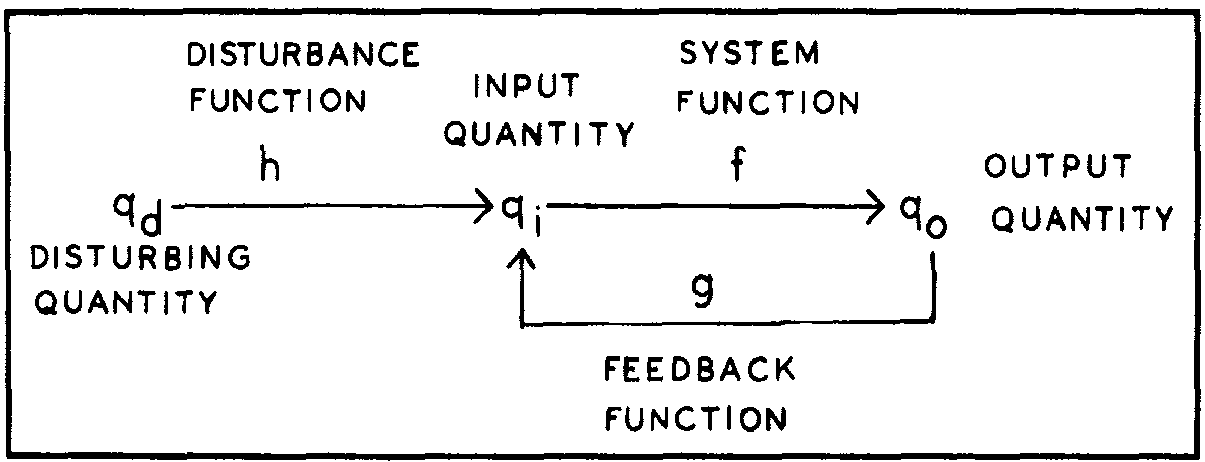
RM: The function qo = f[h(qd)] is the organism function from the point of view of scientific psychologists who view organisms as Z-systems.
Well,that is the solution of a Z system, in terms of the 1978 paper, it is NOT the organism function. From the point of view of scientific psychologists, it is something like R = O (S), they don’t usually speak about disturbances or quantities, etc.
RM: This equation is equivalent to the organism function in equation (1) because qi = h(qd) and experimental psychologists assume that h() is a multiplier of 1.
Good. For no feedback effects in a Z-system, qi = h(qd) is correct.
RM And Bill certainly does refer to the f function in the equation for a Z-system – qo = f[h(qd)] – as “the organism function” when he says " …the organism function f in the Z-system equation is replaced by the inverse of the feedback function g-1 in the N-system equation".
Yes, he refers to F as the organism function.
He does not refer to qo = f[h(qd)] as the organism function, as you claimed two posts ago. There is no other organism function in the 1978 paper. Glad we have that settled. You were not doing damage control, you really misunderstood the text.
RM: That’s mathematically correct because you have defined qe = h(qd). This hides the fact that it is qd – not qe – that is manipulated in a psychology experiment. Thus, you have effectively “buried the lede” of Bill’s paper, which is as follows: The foundation of experimental psychology is that DV = f(IV) or, in Bill’s terms, qo = f(qd), where f() represents functional characteristics of the organism under study.This foundational assumption is wrong if organisms are N-Systems.
In Bill’s terms, it is qo = F(H(qd)), so bold is not quite correct. If you put H(x) = x, then it is correct.
Also, for H(x) = x, you get a nice: qe = qd, so you can replace qe with qd in the equations of Z-systems.
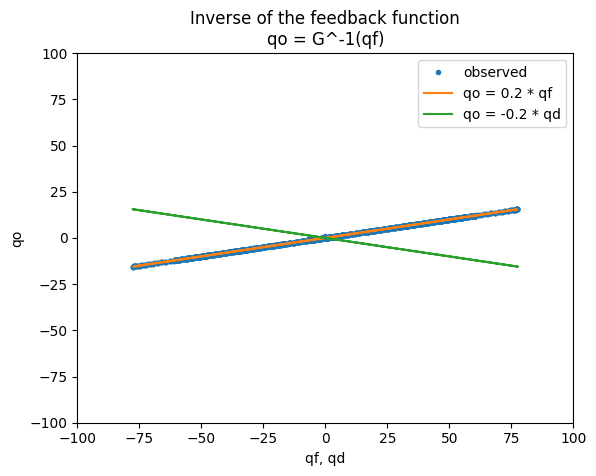
RM: Conventional psychologists can’t be looking at qo = G^-1(qe) or qo = F(qe) because they can’t see qe !
Sure they can, qe is H(qd), by definition. You claim explicitly “RM: experimental psychologists assume that h() is a multiplier of 1.”, so qe = qd, and all the equations hold, and the experimental psychologists are really seeing qo = G^-1(qd), while they think they are seeing qo = F(qd).
If the H is not really the multiplier with 1, but some other function, they will absolutely see qo = G^-1(qe), or equivalently qo = G^-1( H(qd)), while they might think qo = F(qd).
But you’ve missed the point:
They are looking at qo = G^-1 ( H (qd)).
They think they are looking at qo = F(H(qd)).
There, now with H. The only difference between these two equations is that the F is replaced by G^-1. That is the behavioral illusion. Taking a wrong model, a zero feedback system, as the model of organism behavior. That is the point of the whole section of the 1978 paper that talks about the behavioral illusion, although not the general point of the paper.
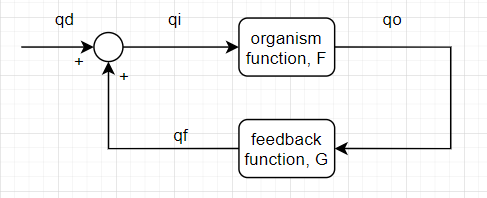
RM: inverse of the feedback function that relates qo to qi.
Nope. The feedback function relates qo to effects on qi. The organism function F relates qo and qi.
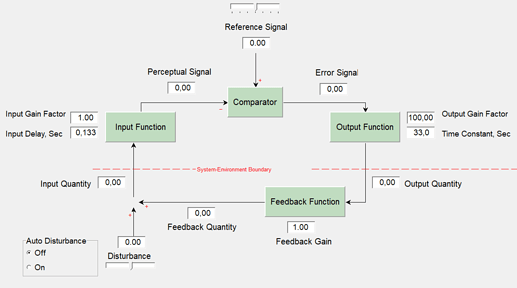
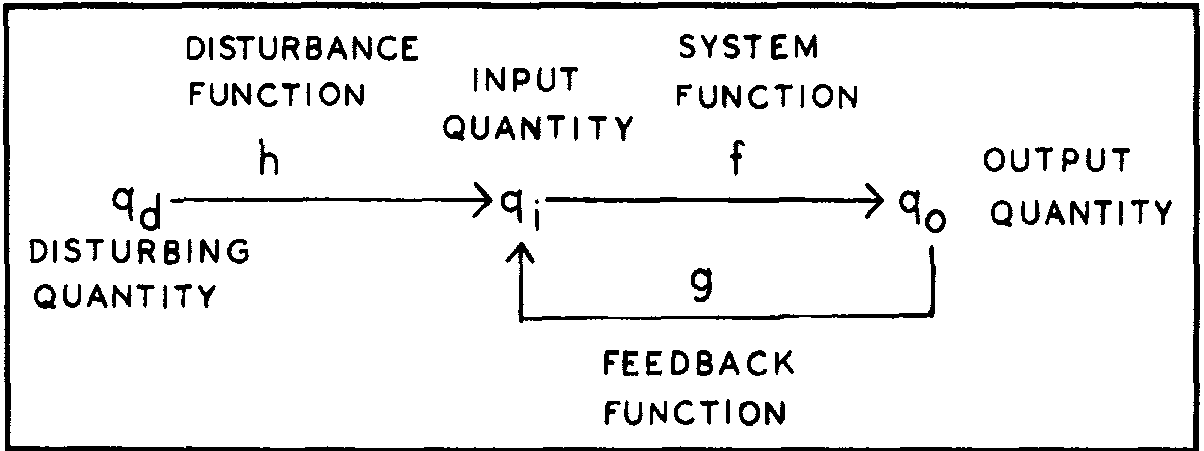
Organism function: qo = F(qi)
Feedback function: qf = G(qo)
Disturbance function: qe = H(qd)
Environment function: qi = G(qo) + H(qd), or equivalently: qi = qf + qe
RM the main point of Powers’ 1978 paper, which is: You can’t tell anything about the behavior of a living control system – an N-System – by studying relationships between independent (stimulus) and dependent (response) variables. In order to understand the behavior of a living control system you have to determine what variables it is controlling. This is the truly revolutionary point of PCT.
That is good, the bold part. I agree that is one of the main points of the paper. There are many other minor points, one of which is the behavioral illusion (topic of the current discussion), and others are various blunders and mistakes.
The preceding part is complete nonsense:
RM You can’t tell anything about the behavior of a living control system – an N-System – by studying relationships between independent (stimulus) and dependent (response) variables.
Qd and qo are stimuli and responses. The tracking task is a careful examination of the relationship between a continuous stimulus and continuous response. Any test for the controlled variable is going to be conducted by applying a stimulus that possibly disturbs the controlled variable and examining the relationship between the stimulus and the response, and other variables we can calculate from the stimulus, the response and our model of the system, including the hypothetical controlled variable qi. If the response ‘cancels’ the stimulus, and qi is near zero, that is a good hint we found the controlled variable, for example. But we are still doing stimulus-response experiments. The difference is that stimuli and responses are continuous, so we allow feedback from the behavior to the controlled variable, and we study individuals and their behavior, and not averages of stimuli and responses in groups.
You need to find a better way of saying the sentence I quoted. Maybe: “You can’t find the organism function by looking at the S-R plot”. or “S-R experiments focused at finding controlled variables can reveal important things about the organism”
RM: The behavioral illusion doesn’t result from an error in system identification; it reveals an error in system identification. And it shows that this error in system identification results from failure to see that the system is a control system
“System identification” in this context means identifying the system, organism, as a Z or N system. so your second sentence is “And it shows that this error in system identification results from a failure of system identification.”
Yes, I agree. An error in system identification is an error in system identification. They did not notice there is feedback in behavior, or they did not think it is important. Their error is possibly going to result with the behavioral illusion, if they claim they found the organism function in the S-R relationship, and then we can reveal the error by pointing out “hey, that is a behavioral illusion, your S-R relationship will change when you change the environment feedback function G”.
RM: I did that on purpose because I was well aware of the fact that the power law is not an example of the S-R illusion that Powers describes in the 1978 paper. In both of our papers on the power law I tried to make clear what we meant by “behavioral illusion”. Here’s a quote from the second paper: " …a behavioral illusion occurs when an observed relationship between variables is seen as revealing something about the mechanisms that produce a behavior when, in fact, it does not". The power law (like the S-R illusion) is a behavioral illusion in this sense.
Hm. So, you quote the 1978 paper for people to look up the definition of the behavioral illusion, which is taking the observed S-R relationship as the organism function F when the S-R relationship reveals the inverse of the environmental feedback function G.
Then you redefine behavioral illusion to be different from the 1978 definition. Instead of the “organism function” you put “something about the mechanisms that produce behavior”.
Why the redefinition while still quoting the 1978 paper? Why even call it “a” behavioral illusion, instead of just “statistical artifact”. This way is sounds like the the 1978 behavioral illusion is just some statistical artifact.
RM: Reaction time is not a side effect of control; it is as aspect of control system operation.
Sure it is. The main effect of control is keeping the controlled variable stable or at reference level. All other effects are side-effects. And many times, they do reveal something about the organism or the “mechanisms that produce behavior”.
I don’t know where you get this silly idea that side effects don’t tell you anything about the system. They don’t tell you what is the controlled variable, and that is the main thing to discover, I agree, but the various side effects can certainly be useful in finding other parameters of the system. After finding the controlled variable, you can look at responses at different frequencies, examine delays, speeds, amplitudes… All reveal something about the system, while not being the main effect.