Hi Adam
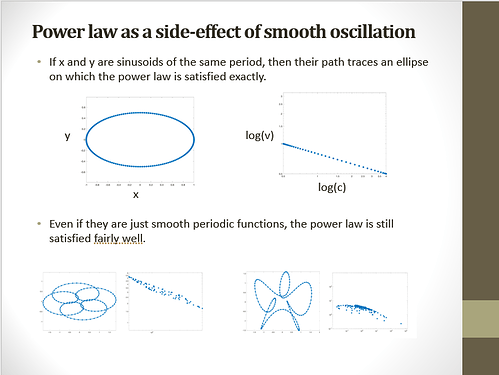
RM: Again, I want to publicly admit that I was wrong to say that the power law is a statistical artifact. It is not and I apologize for saying so. My only excuse is that I was seduced into thinking so because of the fact that the coefficient of curvature in the mathematical relationships between measures of curvature (R, C) and speed (V, A) of movement are 1/3 and 2/3, exactly the values that had been proposed for the power law. I still think it’s a weird coincidence that the observed power law values are close to those values but your demonstration convinced me that the usual single variable regression of log curvature on log speed give an accurate measure of the beta value of the actual power relationship between curvature and speed. I still think that the observed power law is an irrelevant side-effect of controlling for the production of curved movement and is, therefore, an example of a behavioral illusion. But it’s not because the power law itself is a statistical artifact.
RM: I believe that is true for Bill’s model and your copy of it but it can’t possibly be true for Viviani’s model, can it:
AM: Sure it can. Bill’s model can be written in one line as
F = Kp * Kv * C_T_distance - Kv * velocity_of_the_cursor
AM: Viviani’s model is:
A = alpha * C_T_distance + beta * C_T_velocity_difference.
If we put pos_output = vel_reference = alpha * C_T_cistance, then
A = vel_reference + beta * (C_T_velocity_difference)
RM: The problem with this for me is that it conceals the architecture required to implement this model. You need two hierarchically related control systems to implement Bill’s model because C T distance in Bill’s model is actually the difference between the perception of C and the reference for C determined by the system itself. The resulting C T distance is then an error signal that becomes the reference for the lower level velocity control system.
RM: In the Viviani system you don’t need a higher level system if C T distance is considered to be the perceived error that becomes the reference for the velocity control system. This would make the Viviani system a hybrid S-R control system with C T distance being the stimulus that causes the reference to the lower level velocity control system as the response. And the velocity control system would be the control system component of this S-R /control system hybrid. This could easily be shown to the the wrong model by simply asking the subject to keep the distance between C and T at some value other than 0. To account for this you would have to have a separate control system controlling C T distance.
RM: In what way does it work for squiggles and not work for non-squiggles?
AM: It works in the sense that it behaves similarly to human subjects in the same tasks of following targets along non-predictable squiggly paths, and it does not work for non-squiggles or “predictable” movements or patterned movements, because it does not behave very similar to human subjects in the same task.
RM: This is a well known phenomenon. Conventional psychologists would solve it by putting prediction into the model; PCT would solve it by assuming that the subject is controlling a higher level perception, which is the observed pattern of movement.
RM: And the model with varying reference does show that the changing reference state of the cursor is a controlled variable and that the movement can follow a power law while the actions that produced it don’t.
AM: What is the controlled variable?
RM: One is the position of the cursor and the higher order one is probably the pattern of movement being produced.
AM: Does the reference already contain a correlation between speed and curvature?
RM: Yes, because there is a correlation between speed and curvature for all curved movements.
AM: Actions are the same as the movement in all Bill’s models that I know of, and the speed-curvature power law is found in actions=movements. If the actions are forces, why isn’t there a calculation of accelerations, then an integration between accelerations and velocity, and another between velocity and position?
RM: This is not really necessary when modeling things like tracking a cursor on a computer screen. The dynamics are absorbed into the output function. I think it would be necessary (and enlightening) if the tracking were done with a joystick whose resistance to applied force could be varied. Then you could presumably show control of joystick position by varying the resistance of the stick (a disturbance to joystick position) and at the same time show control of cursor position by varying a computer generated disturbance to cursor position. What you should be able you could show (and model) is two nested levels of control happening simultaneously. I don’t know if anyone has done this but I bet, with your skill, you could easily do that in your lab.
AM: Though, in a general sense, the position control model is a good start because it has been proven to model human behavior in many experiments with random-moving targets. If we take that model as the starting point, along with the idea of the hierarchy, then, of course, the reference for the position is changing as the output from a higher level. That is almost an apriori start from the “PCT perspective as I see it”.
RM: Completely agree!
AM: The question is then, what sort of variables can be controlled so that their output creates a varying reference signal for position control, that further results in actions that follow the power law.
AM: If the reference is set by the modeler, and it already contains the power law, that doesn’t seem like a very general solution.
RM: But what if that’s what the subject is doing – varying their reference for position in a way that produces trajectories that sometimes come close to a power law? I think the goal should be developing models that match the behavior of the subject, whether the subject’s behavior matches a power law or not.
AM: For each movement, say, different speeds of drawing an ellipse, or different shapes, like numbers or letters, the modeler would need to set up a new reference signal that results in a movement similar to the movement of human subjects. Really, the modeler is doing all the controlling when he is setting up the reference signal, and when he is not involved, the loop of the model is open.
RM: I know how you feel. We want our models to fit the data without putting the data itself into the model. And this is a particular problem for PCT because the controlled results we see often depend on people varying their references in a way that corresponds to the results we see. But I think there are ways to get around this. One is by doing experiments like the ones done by Viviani and Stucchi, where the subject can control a variable without having to produce the outputs that are typically used to control the result. So have the subject control a movement by pressing keys that affect the parameters of the observed movement rather than by moving a finger. Another way is to have the subject produce the result in the usual way but in the face of measurable disturbances and see if the model deals with them as expected if it were controlling a particular higher level variable.
RM: There are ways to do this; at least I trust that there are. Otherwise, PCT is untestable, a possibility up with which I will not put.
Best
Rick
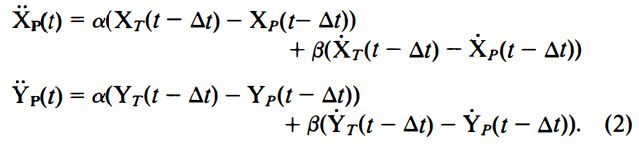 ; the reference for
; the reference for