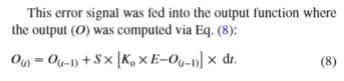Delay in control loops

[bnhpct]

“Sensorimotor delays in tracking may be compensated by negative feedback control of motion-extrapolated position”
https://rdcu.be/b9CWv

Brilliant, Warren. Congratulations!

We simulated human tracking of repeating and non-repeating patterns with two control models, one using only feedback of target and cursor positions, and the other also utilizing target velocity information to anticipate target motion. Both tracking and simulation results appear to indicate that participants exploit local target velocity when tracking targets that move in repeating patterns. Conversely, we did not find evidence that participants use this strategy when nonrepeating, pseudorandom targets—despite the availability of velocity information in both cases.

A perhaps unexpected result: Projecting the future position of a rapidly-moving target, including the ‘illusory’ (i.e. imagined) visual perception of its location, sure looks like a form of imagination as experienced subjectively. This challenges dogmatism that the mechanism of imagination must involve copying reference input to perceptual input. That is a proposed model of a type of imagination, not a complete model of all forms of imagination.

Such compensation can be observed readily in the ‘flash-lag’ effect, an illusion in which a continuously moving target is observed to be advanced in position to a sudden onset target presented in-phase (Nijhawan 2002). The illusion may be explained by a tendency for humans to extrapolate target motion to mitigate sensorimotor delays in perception.

Related:

• Loop delay and limits on control
• Delay in human controller
• Control loop delay, Perception study
• Predictive control; brain function; loop delay

[amatic]

Great finding!

The spreadsheet linked in the paper demonstrates really well how the model behaves and how close it follows the target:

Spreadsheet analysis of position extrapolation

[wmansell]

Thanks for initiating this discussion. Max did a fantastic piece of work on this. We thought it was important to do given the long-standing claims against PCT and other negative feedback control systems based on sensory delays. It’s a shame we couldn’t include additional disturbances in the research to show the PCT model’s additional simultaneous robustness to other modalities of disturbances, but this study was hard to run as it stands!

[rsmarken]

@wmansell

WM: It’s a shame we couldn’t include additional disturbances in the research to show the PCT model’s additional simultaneous robustness to other modalities of disturbances, but this study was hard to run as it stands!

RM: It’s a shame that you didn’t add a disturbance to cursor, C, position. If you had you would have found that the target, T, extrapolation model actually performs considerably more poorly than a simple, leaky integration model that controls T - C, even at delays greater than 100 msec. And I’m sure that the control of T-C model would have fit the individual subject data better than any version of the target extrapolation model.

Best

Rick

[wmansell]

Hi Rick, as you probably can see from the article, the position extrapolation model does use leaky integration to control T-C. I’ll ask Max if he’s got time to mock up a simulation to compare the two models of leaky integration of T-C control, with vs without position extrapolation, sine vs pseudorandom target, with vs without additional pseudorandom disturbance to cursor movement. It would be great to test this empirically.
All the best
Warren

[wmansell]

But we’d need a new human participant study to test the match with actual performance. Mmm, need a new Masters student…

[amatic]

I’ve started working on replicating the model yesterday, works great on sine waves. I have some data from various tracking studies from the lab, so I’ll check how it does, and how well I can fit it.

As far as adding a disturbance to the cursor, that is a different situation than if the disturbance is simply the target position changing. Different variables could be controlled in different situations, and it seems like target speed + position difference (both perceived with a delay!) works really well. Remains to be seen what happens in other situations.

RM: And I’m sure that the control of T-C model would have fit the individual subject data better than any version of the target extrapolation model.

You’re sure? We are playing science here, not speculation. Show the evidence.

Not saying you are wrong, though, the model might be performing worse than the T-C model in pursuit tracking with cursor disturbance added, and better in a situation without the cursor disturbance. Even if it does, it would still be a great model for the ‘pure’ pursuit task.

[MParker]

Hi all,

First off, thanks for your interest in the article!

I’ll make a simple simulation with leaky integration in both models. Of course, this is the case in the article but not the spreadsheet analysis for simplicity.

It is, for sure, an interesting question of the utility of motion extrapolation in the presence of an unseen disturbance to cursor position. I would say that it is clear (from the article) that humans do not use motion extrapolation when things become more unpredictable, even when this approach would be beneficial for a model. It seems to me to be likely that the utility fades with increasing unpredictability, whether that is within the target signal or because of an unseen disturbance. I would think that in most tracking applications endogenous disturbances are quite small relative to target displacements, and so motion extrapolation may be useful in many cases.

It strikes me that it would be very interesting to conduct a pursuit tracking study with sinusoids or ellipses in which the characteristics of a cursor disturbance are manipulated, particularly the amplitude, and the tendency to use motion extrapolation is measured. The model-based analysis here should be simple, I’ll try it out.

Best wishes,
Max

[MParker]

Hi Rick & others,

@rsmarken

RM: It’s a shame that you didn’t add a disturbance to cursor, C, position. If you had you would have found that the target, T, extrapolation model actually performs considerably more poorly than a simple, leaky integration model that controls T - C, even at delays greater than 100 msec. And I’m sure that the control of T-C model would have fit the individual subject data better than any version of the target extrapolation model.

In fact, I have just checked this and it is not the case that the position control model is more resilient to cursor disturbances. In fact, they are equally affected by the disturbance and the position extrapolation model performs more accurately (correlation) for a range of disturbances, due to its ability to compensate the delay.
Here’s a graph:

Blue is the target signal, orange line is the extrapolation model, green is the position control model and the red is the disturbance waveform, The correlation between the orange and the blue was .992 and between the green and blue .978.

I conducted these simulations in Python so that the source code is freely available:

GitHub - maximilianparker/Tracking_python: Models of compensatory and pursuit...

The parameters of the models can be altered alongside whether the task was compensatory or pursuit (of course it makes no difference in compensatory as there is no target velocity).

Cheers,
Max

[rsmarken]

[quote=“amatic, post:7, topic:15691, full:true”]

RM: And I’m sure that the control of T-C model would have fit the individual subject data better than any version of the target extrapolation model.

AM: You’re sure? We are playing science here, not speculation. Show the evidence.

RM: The way I and the people I admire play science we make predictions about how the model will fit the data. Then we test those predictions. None of that was done in this research.

[rsmarken]

@MParker

MP: In fact, I have just checked this and it is not the case that the position control model is more resilient to cursor disturbances.

RM: I get the same result. But that is only if I use the leaky integration approach to producing output, as you did in the python model. In that case the models with and without “extrapolation” are essentially equivalent (though, as you say, the extrapolation model has a slight advantage; I find that when the disturbance to the cursor is 10% of the target range the extrapolation model does .16% better than the non-extrapolation model in terms of rms error; when there is no disturbance to the cursor the extrapolation model does 35% better).

RM: By the way, I put extrapolation in quotes because your model is not really making an extrapolation; it is controlling a present time perception that is (T + dT/dt) - C.) The big difference in tracking performance that I found earlier is between a leaky integration (slowing) model that controls T-C and your more pure integration model in the spreadsheet that controls (T + dT/dt) - C).

RM: So what you could do, given that you have all this performance data from humans, is test to see whether a leaky integration model controlling (T + dT/dt) - C) fits the human data better than the equivalent leaky integration model controlling just T-C. Since the big difference in performance of those two models occurs when there is no disturbance to the cursor, you could do this test for the controlled variable with the data you have. You could test to see whether the controlled variable is better defined as (T + dT/dt) - C) or just (T-C).

RM: If you do that I would be interested in seeing how it comes out.

Best

Rick

[MParker]

Hi Rick,

Glad that you got similar results. Yes, I think the real advantage of extrapolation is with regard to delays, not to countering disturbances. The point in the paper is that the feedback delays are likely to be around 100 ms as a minimum, and that for sinusoid targets and ellipses, participants do not show a response delay even this long, meaning that their feedback delay has been comprehensively compensated in that case.

Yes, I agree that it is a present-time integrated perception where target position is biased. The whole idea is that it is plausible within the PCT framework and does not require internal models blah blah.

@rsmarken

ng just T-C. Since the big difference in performance of those two models occurs when there is no disturbance to the cursor, you could do this test for the controlled variable with the data you have. You could test to see whether the controlled variable is better defined as (T + dT/dt) - C) or just (T-C).

Just to be clear, in the EBR article both models had a leaky integrator (slowing factor) and so the comparison there is exactly as you describe (though without a disturbance as you have pointed out). In contrast, the spreadsheet was a simplification and did not include a leaky integrator in either model.

The main findings of that paper were

1. For pseudorandom signals the position extrapolation model fits no better than the usual position control model (both with leaky integrators) - indicating that participants do not use extrapolation when tracking these targets.
2. In contrast, the position extrapolation model is a better fit to the participant data when loop delays are sufficiently long. The breakdown of results into phase differences and amplitude ratio shows that the benefit is entirely due to delay compensation - indicating that it may be the case that participants make use of target velocity (in addition to position) when tracking these targets.

Cheers,
Max

[amatic]

Btw. there is a missing parenthesis in the output function on the diagram,

The text gives a different equation

Maybe that is where the confusion is with the leaky integration.

[rsmarken]

@MParker

MP: Glad that you got similar results. Yes, I think the real advantage of extrapolation is with regard to delays, not to countering disturbances.

RM: Yes, but the improvement in tracking ability with respect to delays is very small relative to what you get just from control using a leaky integrator. And it’s especially small when a disturbance is added to the cursor.

MP: The point in the paper is that the feedback delays are likely to be around 100 ms as a minimum, and that for sinusoid targets and ellipses, participants do not show a response delay even this long, meaning that their feedback delay has been comprehensively compensated in that case.

RM: But we already know that from all the modeling that has already been done. A leaky integrator control model typically fits the data extremely well (r>.99) with just a leaky integration in the output and not transport lag. Adding a transport lag produces very little change in the fit to the model. So the fact that there is a neural transport lag on the order of 100 msec in a tracking task has already been shown to be no problem for a control model.

RM: The only reason I posted my comment about your article was to try to encourage you to use your research skills to do PCT-based research – research aimed at testing for controlled variables.

MP: Just to be clear, in the EBR article both models had a leaky integrator (slowing factor) and so the comparison there is exactly as you describe (though without a disturbance as you have pointed out). In contrast, the spreadsheet was a simplification and did not include a leaky integrator in either model.

RM: Yes, I’m afraid the spreadsheet misled me; because of the huge effect of the disturbance to the cursor I assumed that your model was not controlling T - C when, in fact, it was; the huge effect of the disturbance that I found for your extrapolation model compared to my non-extrapolation leaky integration model was a function of the difference in the nature of the output functions.

MP: The main findings of that paper were

1. For pseudorandom signals the position extrapolation model fits no better than the usual position control model (both with leaky integrators) - indicating that participants do not use extrapolation when tracking these targets.

RM: It looked to me like you were measuring the fit of model output variations to target variation. I wasn’t able to find any reports of measures of the fit of the model to individual subject behavior.

MP: 2. In contrast, the position extrapolation model is a better fit to the participant data when loop delays are sufficiently long.

RM: So you did fit the model to the participant data? I can’t find reports of such fits in the report.

MP: The breakdown of results into phase differences and amplitude ratio shows that the benefit is entirely due to delay compensation - indicating that it may be the case that participants make use of target velocity (in addition to position) when tracking these targets.

RM: If that’s the case then the “extrapolation” model should provide the best fit to both the sine and pseudo random target tracking data for the subject’s. This is because the subjects’ neural transport lag was the same in both sine and pseudo-random target tracking and if extrapolation is a hedge against transport lag it would be controlled in both cases. Is that what you found? If the extrapolation gave a better fit in the sine than in the pseudo random tracking situation then it certainly has nothing to do with delay compensation.

RM: At the risk of eliciting more profanity from Mr. Matic I predict that “extrapolation” provides the best fit to the subjects’ behavior only when they are controlling the sine wave target, not the pseudo random target. And that’s because with the sine wave target the subjects are able to control for a high level perception of “extrapolation” – probably something like dT/dt – by varying cursor position appropriately.

Best

Rick

[amatic]

Rick, [insert profanity] read the paper. You’re mixing (1) phase delays between the target and cursor sinusoids with (2) feedback transport delay. No point in discussing the paper if you are not going to read the thing. There are also comparisons of fit between the model and subjects for random and sinusoid inputs [more profanity].

The [C-T distance + Tv] is a pretty regular type of a controlled variable, no need for higher levels or nothing like that. The target is visible, the cursor is visible, all information is available on the screen from vision.

A great demonstration of how to do the TCV for tracking sinusoids! It never occurred to me to try target velocity, even though I tried cursor velocity and (T-C) velocity.

[MParker]

@amatic

Btw. there is a missing parenthesis in the output function on the diagram,

Frustrating that I missed this in the proofing process! Thanks for pointing that out Adam!

[MParker]

Rick,

Yes, the comparisons of model simulated cursors and participant cursors were conducted and are presented in the line graphs, The bar graphs show the fit of the participant cursors to the target.

I don’t disagree that the position control model fits the behaviour well as per the correlations, however, I would say that correlations are a poor measure of temporal asynchrony in tracking (as is RMS as demonstrated in the paper). The leaky integrator position control model is unable to compensate transport delays effectively and the extrapolation model performs substantially better under conditions of delay. In fact, this is a challenge for the position control model because:

• The transport delays are non-negotiable
• despite the transport delays participants sometimes track without a delay
• The position control model cannot compensate this delay

I disagree that the extrapolation model should necessarily have a more accurate fit to both sinusoid and pseudorandom cursor data. I expected that it would because velocity information is available in both cases. However, given that participants don’t exhibit zero phase tracking when tracking pseudorandom signals (they track with a phase delay of about 180ms) this demonstrates that they are not compensating their intrinsic transport delays (as they must be when tracking with <100 ms phase delay for sinusoids). The fact that participants do not appear to utilise velocity information when tracking pseudorandom targets is noteworthy and several potential explanations for this are set out in the discussion…

So yes, the neural transport lag is the same in both cases, but the participants only compensate it when tracking sinusoids (as is seen in their behaviour, irrespective of the model), and suitably, the extrapolation model only fits the cursor data better in that condition.

It may be the case that controlling higher level perceptions could also provide this ability, controlling for the long term pattern of the repeating sinusoid, for instance. One interesting thing, as Adam said, is that controlling cursor velocity - target velocity error does not confer the same advantage (I tried this before simply the target velocity).

Best,
Max

[amatic]

I’ve been trying out some things with elliptic target tracking data. This was just me, tracking the target on the screen, using a graphics tablet and a pen, like this one:

Some example data:

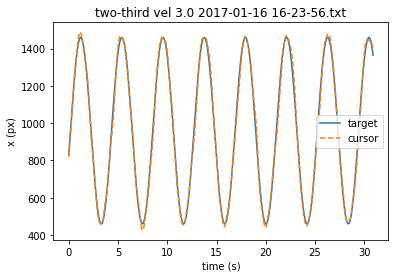
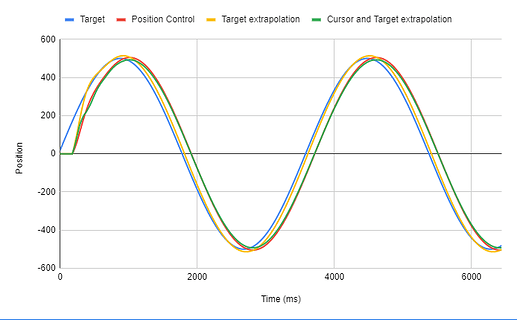
The two-third in the title is related to the power law stuff, for the x and y data it means that the trajectories were pure sinusoids when plotted against time like in this plot. This was one of the slower targets, vel 3.0 which looks like 0.2Hz or so.

The situation is not quite like tracking sinusoids in one dimension, since there might be more information in the visual scene for the participants to see and control, but let’s say it is similar if we decompose the trajectory to x and y over time.

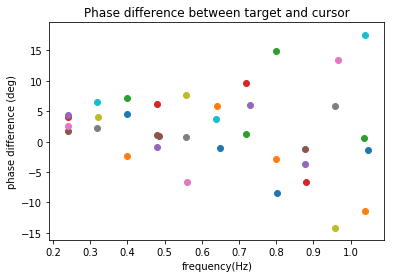
The phase difference is near zero, with a larger variance at higher speeds.

You also got fairly small phase differences, but were they negative for any cases? I seem to get them about the same amount as positive ones, especially for high-frequency targets. This would mean that on average the subject was leading in front of the target.

Btw. I used curve-fitting to find the phase, frequency and amplitude of the cursor and of the target wave, and then calculated the difference of the phases. I did not use FFT. The amplitude seems to be 1:1 between cursor and target.

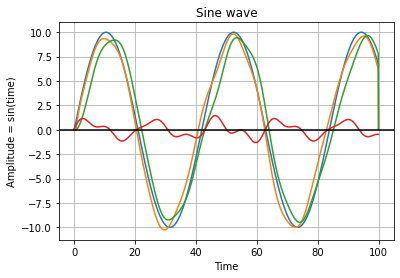
Next I tried running the two models against the target and comparing them. The extrapolation model seems better than just position difference. Here is one example of comparing the fit between the two models and the cursor:

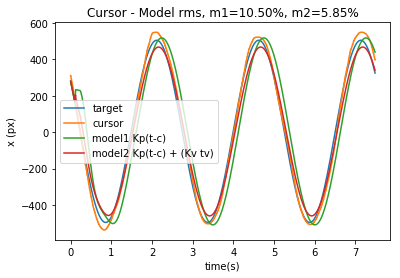
The red line is closer to the yellow line than the green one, meaning the model2 is fitting subject behavior better than model1. I’ve moved the curve to be centered at 0 px.

Here are the results for all tracks:

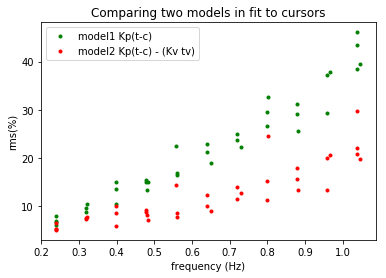
Lower is better, so all the model2 runs seem to fit better than model1 to subject behavior.

I’ve used Kp=8, delay=0.125ms, for model1 and model2. In model1, the damping gain is 0.2, in model2 the damping gain is 1.2, and the Kv = -130.
Though, maybe Kv should be multiplied by dt (which was 0.005). I did not change these parameter values between runs.

What parameter values would you say fit subject behavior best for the extrapolation model?

So, looks like a pretty good improvement over the t-c model for sinusoid tracking.

I was digging through the archives too. I remember reading that Bill had some ideas about extrapolating velocity when tracking targets.

[From Bill Powers (950529.1230 MDT)]
Hans Blom (950529) –
Nothing of this is new, of course.

1. Tracking a regular (“predictable”) pattern with approximately zero delay has
   frequently been encountered in human operator response speed studies.

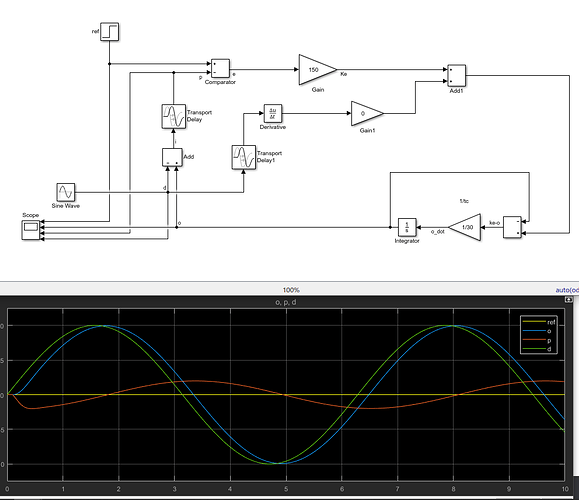
You will find a demonstration of this effect in the 1960 paper by myself, Clark, and MacFarland. This can be be explained, as I said, using a hierarchical model. The first level is an ordinary control system controlling the cursor used for tracking. The second level perceives the synchronization of the cursor and target movements (the principle of the phase-locked loop will serve as the perceptual function), and the output function consists of a variable-frequency variable-amplitude oscillator which varies the reference signal for the cursor-position control system. This will achieve approximately zero average delay, without needing the kind of world-model in your program.

If the target moves in a sine-wave, there is an even simpler way of achieving zero delay, even with a single-level system. Simply add some first derivative to the perceptual signal representing target-minus-cursor. This can actually result in the cursor movements occurring slightly ahead of the target movements – a negative delay! We would use that model, of course, only if the real human
behavior also showed a negative delay.

[From Bill Powers (2005.02.15.0816 MST)]
[…]
What do we mean by “predicting?” One meaning is surely to make a statement or form an expectation about something that hasn’t happened yet. But another is simply to act on the basis of the extrapolated future state of some variable – i.e., its first derivative times some adjustable constant, added to its present state. That’s how “anticipation” works in heating and cooling systems, and elsewhere. The effect of prediction or anticipation in this latter sense is, as we often find in control systems, the opposite of what
intuition suggests.

[amatic]

Btw. Max, did you use Matlab’s Simulink for modeling?

I’m just learning it. The lower right part is the leaky integrator output, there is probably a better (simpler) way of modeling it. The target speed gain is 0.

And then in this one the target speed gain is larger, looks like zero phase difference.