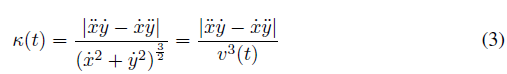Discussion of the speed-curvature Power Law

Research Motor control
61

I think it’s been very fruitful, for me anyway.

I wish you would restate the mistake that we made that Moaz et al didn’t. As I pointed out earlier in an equation-by-equation comparison of the Marken-Shaffer to the Moaz et al analysis, the two analyses are identical. So if you and/or others have shown the mistake we made that Moaz et al didn’t make I apparently didn’t catch it or understand it. So I would really appreciate it if you (or someone else) would show me again the mistake that we made that Moaz et al didn’t make. I think it’s very important becuase if you are correct then OVB analysis cannot account for the power law, it would be disappointing but illuminating.

62

I don’t know how much more often I have to point out the error I first described in my published comment, that you say that if X happens to fit an equation, X therefore is THE ONLY solution to the equation. How many more times do you want me to repeat the same thing in different words? I’m not sure if I can find a new way to say it that I haven’t used in the dozens of attempts to get you to understand. I tried, for example, to use an analogy such as if you see a brown dog, it is NOT necessarily true that all dogs are brown.

63

I want you to show me exactly where Marken & Shaffer make a mistake and Maoz et al don’t. No general statements. Just show me exactly where it is in Marken & Shaffer and isn’t Maoz et al. It should be easy to do; you can apparently see it in the two papers. I can’t. So just show me.

64

It would be easier if you told me what you didn’t and don’t understand about when I did exactly that. It’s in the archives somewhere, and I can’t be bothered going over it all again. Repeating what already has been discussed is boring, and I have other fish to fry (PPC, for example).

65

Oh no, Rick, now again you dismiss answering the criticism and just repeat your own opinions. This thread is again a new example of that worst dysfunction in our discourse. This is not what scientific discussion should be. Popper says nicely in his Conjectures and Refutations: “the dogmatic attitude is clearly related to the tendency to verify our laws and schemata by seeking to apply them and to confirm them, even to the point of neglecting refutations, whereas the critical attitude is one of readiness to change them–to test them; to refute them; to falsify them, if possible. This suggests that we may identify the critical attitude with the scientific attitude, and the dogmatic attitude with the one which we have described as pseudo-scientific.”

RM: Well, Eetu, if the spreadsheet doesn’t convince you that the power law is a statistical artifact…

Thanks again for the spreadsheet. It clearly shows to me and hopefully to others too that your fabricated “true” relationship coefficients between the sides of random quadrangles or between velocities and curvatures of random trajectories are statistical artefacts.

RM:… – a side effect of control that is explained by how researchers have measured it…

You should finally believe that no one here is seriously claiming the power law phenomenon being anything other than a side effect of control. The disagreement and discussion has been mainly about your faulty and contradictory argumentation.
For example if something is a statistical artifact then it is either a side effect or a main effect of the control of someone using statistical methods wrongly – not a side effect of the control of the subject moving in a curved trajectory. According to Oxford reference: “A statistical artefact is an inference that results from bias in the collection or manipulation of data. The implication is that the findings do not reflect the real world but are, rather, an unintended consequence of measurement error.”

RM: … – then I will no no longer try to prevent you and your humting party from stalking that Boojam.

Behavioral illusions is an interesting but totally different topic of discussion.

RM: l just note that I can’t claim credit for inventing Omitted Variable Bias (OVB) analysis. This tool, which you believe is used “to prove true something which is not true,” was “invented” some time ago by others.

Your “OVB analysis” is not at all what those others are talking about. A better name to your method is “DVB fabrication” from Doubled Variable Bias. You create a bias by adding both the dependent and the independent variable (in addition to the independent variable) to the predictor side of the regression analysis. (Your “omitted variable” D is the product of the curvature and the velocity to the power of three.) It is possible that some real variable is missing, but if it is then it should be searched for, not fabricated.

RM: And though it was not called by that name, OVB is the analysis of the power law that was described by Moaz et al (2006) well before I descsribed it in Marken & Shaffer (2017).

Maoz et al did not even try to use that DVB fabrication method. Only common thing between your article and theirs is the equation of D. They did not make any such questionable claims and inferences from it as you do. So you cannot push the responsibility of your fabrications to them.

Now, could you finally answer to the criticism like a scientist would do and not like a politician?

Eetu

66

That is so true and so frustrating! Rick is so strongly controlling for a perception of being right that he cancels all disturbances by turning a blind eye and refusing to perceive them at all. But this is not a private discussion with him and neither just any chatter club. Rather this is or should be a scientific discussion forum and also an introductory area for students, so we should not brook faulty argumentation here, especially when it is repetitive.

67

I don’t understand exactly what it is that Marken & Shaffer (2017) did wrong and Maoz et al (2006) didn’t, since their mathematical analyses were exactly the same.

68

Well, I told you once in some detail, and if it’s too much bother for you to search the archives, I guess you don’t really want to know. You must be controlling not for a perception of your understanding of the difference between your analysis and theirs, but for getting me to waste my time by going through explanations repetitively. And I’m not controlling for reducing your error in that perception.

69

Again? I think I’ve been pretty non-dismissive of your criticisms, going to the trouble of developing a spreadsheet to demonstrate how doing a regression without the omitted variable will produce an estimate of the power coefficient that deviates from its true mathematical value by an amount proportional to the correlation between the included and omitted predictor variables.

I know that you know that the power law is a side effect of control. My " faulty and contradictory" argumentation has to do with why researchers see this particular side effect; something close to a 1/3 power relationship between curvature (C) and velocity (V) of movement. OVB analysis shows that reseachers see this side effect because of the way they measure the relationship between curvature and velocity, using simple linear regression that omits the other variable involved in the relationship between curvature and velocity.

The power law is not a behavioral illusion sui generis. I consider it a behavioral illusion because researchers continue to study it thinking that, if they can figure out why it happens, it will tell them something about how movement behavior is produced. So it’s a behavioral illusion because researchers don’t see the power law as a side effect of control that is irrelevant to understanding how behavior works.

You keep sayng this but you have never shown me where the difference is. I would really like to know. I’m pretty sure there is no difference at all. In a previous post (which I can’t find) I have shown how the Marken & Shaffer (2017) OVB analysis is identical to the Moaz et al analysis. I will have to show the equivalence again in my reply to Martin (coming up soon). After I post that reply, if you can show me exactly how these two analyses are differnet (rather than just saying that they are) I would really appreciate it.

As much as I enjoy being coninually insulted by you guys, I do get a little tired of it. So right now I’m more interested in finding out how the analysis of Marken & Shaffer (2017) differs from the analysis of Moaz et al (2006) than in answering your criticism of my spreasheet demo. I think it is really important for me to understand how these analyses differ if we really want to resolve this conflict. If I could see exactly what Moaz et al got right that Shaffer and I got wrong then I am pretty sure we could have this debate wrapped up with mututal agreement in no time.

70

I looked through the archives and I coudn’t find any post from you that explained exactly how the Moaz et al analysis differs from ours. Indeed, I couldn’t find any post from you that gave any detail at all about what was wrong with our analysis and what was right with theirs. So I’ll do a brief review to show why I think the Marken & Shaffer (M&S) OVB analysis is identical to the analysis done by Moaz et al (Moaz).

Both M&S and Moaz start by deriving equivalent equations for the mathematical relatoinship between curvature and velocity. The Moaz equation is:
image

And the M&S equation is:

image

In both equations velocity is v; affine velicity is alpha in Moaz and D in M&S; curvature is kappa in Moaz and R in M&S (kappa = 1/R hence the negative signe in the Moaz equation).

Next comes the OVB analysis:

In Moaz the OVB analysis is summarized in this equation:
image

Beta is the power coefficient of curvature that will be observed if alpha (affine velocity) is left out of the analysis. Eta is the covariance of the variable included in the regression, log (kappa), and the variable omitted from the regression, log (alpha), divided by the variance of log (kappa):

image

Beta will be equal to its true value, -1/3, if Eta is zero. Deviation of Eta from zero will result in Beta deviating from -1/3.

In M&S the OVB analysis is summarized in this equation:
image

This equation is exactly equivalent to the Moaz OVB equation
image

Our Beta’.obs is equavalent to Moaz’s Beta. Both refer to the value of the power coefficient that will be observed if affine velocity is left out of the regression analysis.

Our Beta.true is equivalent to Moaz’s -1/3, although the value of Beta.true in our case is 1/3 rather than -1/3 since our analysis was done using R rather than 1/R as the measure of curvature.

Finally, our delta is equivalent to Moaz’s Eta/3, as can be seen from this equation in M&S:
image

where Beta.omit is 1/3, the coefficient of the omitted affine velocity variable, and (Cov(I,0)/Var(I) is equivalent to Eta so our delta exactly the same to Moaz’s Eta/3.

This is why it looks to me like the M&S OVB analysis is exactly equivalent to the Moaz et al power law analysis. Now could you please explain to me where we made a mistake and Moaz et al didn’t?

Thanks.

71

Has anyone claimed that your equations are wrong? I don’t think I have. The only thing that’s wrong, in my view, is to claim that if one velocity fits the equations, it therefor is the only velocity that can fit them, whereas with these equations any velocity fits them. Moaz et al. don’t make that claim.

72

Well, here is at least one place where you said “If your power-law theory had used correct mathematics [emphasis mine-RM)], I doubt there would ever have been an issue”, which sounded to me like you were saying my equations were wrong. But here you said “I have never claimed you made a mathematical mistake. I have claimed, and still do, that you interpreted the mathematics wrongly, by making the claims that you consistently have done.”. So what are those “mistaken mathematical claims” that I made that Maoz et al didn’t make. Fortunately you answer right here:

The problem here is that I don’t remember ever having made such a claim. I don’t even know what I would have been claiming if I had made it. Could you please show me where I made that claim? In the meantime, when I have the time, I will explain what both Marken & Shaffer (2017) and Maoz et al (2006) claimed and what they didn’t.

Spoiler alert: Both Marken & Shaffer and Maoz et al claimed that leaving affine velocity out of the regression analysis used to test for the power law will affect the size of the deviation of the calculated value of the power coefficient from 1/3. However, one set of researchers went on to claim that, nevertheless, the power law is not a “bogus” phenomenon while the other went on to claim that it is a “behavioral illusion” phenomenon. Stay tuned to find out who claimed what, and why!

73

Rick and others,

it is the time of the year when relatives are gathering together to celebrate Christmas so I unfortunately seem not to have enough time to write a proper reply before the situation here calms down.

So I just wish you happy Christmas or what ever celebrations you happen to have this time of the year!

74

A reader might be puzzled looking for Greek letter eta here.
ε = epsilon
η = eta
ξ = xi

75

Here is a more explicit statement of Martin’s objection.

76

Thanks for the Greek letter lesson. And thanks for this more detailed description of Martin’s objection to our “math”. It’s quite revealing since, though we didn’t use our analysis on snail and car trajectories, we did use it on helicopter trajectories (see Figure 1 and Table 1 in M&S (2017)) and even discussed the similarity of the results found for the helicopter trajectories to the results found for fruit flies. The relevant discussion is copied here.

image
image708×794 140 KB

It’s true that fruit flies are not snails and helicopters are not cars. But I think this passage shows that we never made the claim attributed to us by Martin, that equation 5 in M&S fits only the velocity profiles found in an experiment.

77

I never said any such thing. But I did try to point out by implication that the limitations that fruit flies and helicopters were constrained, as are cars, by limits on lateral acceleration, whereas snails are not.

78

Now that we all agree, or should agree, that Martin’s objection is without merit, and that the analyses of Marken & Shaffer (M&S) and Maoz et al (Maoz) are identical, I will explain why M&S and Maoz came to diametrically different conclusions about the power law.

First, let me summarize the results of the M&S and Maoz analysis. First, both note that the test for fit of a power function to a movement is done by regressing measures of curvature, C, on measures of velocity, V, of the movement using the following regression equation:

log(V) = log(k) + Beta * log (C) … (1)

If the regression results in a value of Beta close to -1/3 with an R^2 greater than .7 then the movement is consided to be power law compliant. M&S and Maoz point of that equation (1) leaves out a covariate caalled affine velocity, Alpha, which is part of the equation that relates C to V. So the regression equation for power ower law analysis should be:

log(V) = log(k) + Beta * log (C) + BetaA*log (Alpha) … (2)

If you run this regression for ANY movement trajectory, regardless of how it is produced, you will always find that log(k) =0, Beta = -1/3 and BetaA = 1/3. That’s because the true mathematical relationship between V and C includes Alpha:

log(V) = -1/3 * log (C) + 1/3 * log (Alpha) … (3)

Both M&S and Maoz found that when Alpha is left out of the regression used to find the fit of a power law to a movement, the value of the exponent of C that is found by that regression will deviate from its true mathermatical value, -1/3, by an amount proportional to:

Delta = (Covariance [log(C), log(Alpha)] /Variance(log(C)))/3

The size of Delta, for any randomly (or systematically) produced smooth movement is generally very small. Maoz ran several different simulations, generating 100 randomly generated movement trajectories made up of 1,000,000 points in three different ways. The typical value of Beta, averaging over the different types of simulations, was -.31 ± .03 and the average size of R2 was 0.61 ± 0.07. As noted by Maoz “Both Beta and its R2 magnitudes are within what is considered by experimentalists to be the range of applicable values for the power-law”. In other words, you see the power law whether the movement trajectory was generated randomly by a computer algorithm or by a living control system.

I have found essentially the same thing in my own simulations, though I didn’t report them in either M&S paper. What I did show in the M&S paper is that you will see a power law whether the movement was generated by a living organism (human) or a non-living one (a helcopter).

Maoz et al understood the unpleasant ramifications of their simulation studies, as can be seen in the fact that they begin the Dscussion of their results by saying “We do not suggest that the power-law, which stems from analysis of human data, is a bogus phenomenon…”. They say this because they showed that noise added to a non-power law conforming trajectory will produce a bogus power law conforming result. Thus, they conclude that since power law researchers typically low pass filter trajectories produced by living organisms it is unlikely that the power law conforming results they find were produced by contaminating noise.

I find this conclusion very puzzling. Maoz et al have just shown that non-power law conforming trajectories are very rare, as indicated by the very small value (.03) of the standard deviation around the average power coefficient value of .31. Assuming that these Beta values are normally distributed, 95% of the time, for ANY movement trajectory, Beta will be found to lie between .25 and .36. And this range is probably even smaller. As Maoz et al point out “standard outlier detection and removal techniques as well as robust linear regression make Beta approach closer to −.33 and increase the R2 value”. Since observing a Beta close to -.33 is highly probable for any trajectory, filtered or not, it would be impossible to tell when an observed power coefficient is “real” (whatever that means) or a consequence of what Maoz demonstrated earlier in the paper: that the observed Beta is a consequence of omitting affine velocity from the regression analysis.

I also find their conclusion puzzling because they had just shown that the true (mathematical) value for Beta is .33 but that the observed value will differ depending on the covariance between curvature and affine velocity. The filtering procedures described by Maoz can’t protect the researcher from falsely concluding that a non-power law conforming trajectory is power law conforming becuase filtering simply changes the covariance between curvature and affine velocity, and does so in (until some mathemetician figures it out) ann unpredicable way, sometime increasing and sometimes decreasing this covariance (as Maoz et al found out).

Rather than concluding, as Maoz et al did, that the power law is not a bogus phenomenon, M&S concluded that the power law is simply a statistical artifact; a result of omitting afffine velocity from the regression used to determine whether or not a trajectory is power law conforming. Per M&S, the power law is a consistent, but irrelevant, side effect of controlling for the changing position of the moved entity, the change resulting from variations in the agent’s reference for the position of that entity.

The power law is exactly analogous to the word “hello” that is written as a side effect of a person controlling a cursor relative to a target in a demo by Powers (does anyone know where the video of that demo is?). The explanation of that consistent, irrelevant side effect is that the disturbance has been created to vary as the inverse of “hello”.

The explanation of the irrelevant side effect that is the power law is the fact that the method of determining conformity to that law omits one of the variables that determines that value of velocity; this omission leads to a slight deviation from -1/3, the true value of the power relationship between curvature and velocity, but this deviation is typicaly fairly small since in almost all smooth curves the covariance between curvature and the omitted variable, affine velocity – which is the cause of the deviation – is small (as demonstrated by Maoz et al)

Best, Rick

79

RM: Again? I think I’ve been pretty non-dismissive of your criticisms, going to the trouble of developing a spreadsheet to demonstrate how doing a regression without the omitted variable will produce an estimate of the power coefficient that deviates from its true mathematical value by an amount proportional to the correlation between the included and omitted predictor variables.

Yes, you are responsive, friendly and often helpful discusser if there is no disagreement and criticism against your claims. The problem in your responding to criticism is that you just try to prove that you are right, which means just the dogmatic and pseudo-scientific attitude about which Popper talks in the book I cited. Scientific attitude means that we actively search faults in our theories and believe in them only as long as faults are not found (as long as we and others have not managed to falsify them). So if I show that there are error in your claims by stating claims which falsify your claims, you should not only repeat your original claims but instead you should show what is wrong in my claims. In addition, of course, a good theory is one which explains more.

We can clarify your clause:

“doing a regression without the omitted variable will produce an estimate of the power coefficient that deviates from its true mathematical value by an amount proportional to the correlation between the included and omitted predictor variables”

a little by replacing some expressions with clearer ones, which are marked by cursive below:

“doing a regression without an extra predictor variable which is the product of the original predictor variable and the predicted variable will produce an estimate of the power coefficient that deviates from the exponent of the predicted variable in the multiplication equation of the extra variable by an amount (inversely) proportional to the correlation between the included and extra predictor variables”

we can see (and test) that it is true for every possible exponent. But it explains nothing. It namely leaves it unexplained why that correlation varies and thus why the relationship between the curvature and velocity sometimes obeys the power law and sometimes not.

RM: My " faulty and contradictory" argumentation has to do with why researchers see this particular side effect; something close to a 1/3 power relationship between curvature (C) and velocity (V) of movement. OVB analysis shows that reseachers see this side effect because of the way they measure the relationship between curvature and velocity, using simple linear regression that omits the other variable involved in the relationship between curvature and velocity.

So, do you mean that the measurement method creates the power law phenomenon? I can’t really understand your logic. You seem to say that analyzing the relationship between two variables creates the analyzed relationship. But that is not true, at least if the researcher uses the methods according to the proper rules. If we are interested in the empirical dependence relationship between two variables (like velocity and curvature) the standard method for the strength of that dependence is correlation analysis and for the direction the regression analysis between these two variables. We know very reliably that these methods do not create dependencies if there are none in the data. Adding some third extra variables to the analysis can only confuse the relationship between these two variables.

EP: Your “OVB analysis” is not at all what those others are talking about…

RM: You keep sayng this but you have never shown me where the difference is. I would really like to know. I’m pretty sure there is no difference at all. In a previous post (which I can’t find) I have shown how the Marken & Shaffer (2017) OVB analysis is identical to the Moaz et al analysis. I will have to show the equivalence again in my reply to Martin (coming up soon). After I post that reply, if you can show me exactly how these two analyses are differnet (rather than just saying that they are) I would really appreciate it.

We must consider separately the difference between first your mathematical analysis and that of Maoz et al on the one hand and secondly the difference between your “OVB analysis” and real OVB analysis on the other hand. These questions should not be mixed. I will try to show the differences separately below.

RM: As much as I enjoy being coninually insulted by you guys, I do get a little tired of it. So right now I’m more intrested in finding out how the analysis of Marken & Shaffer (2017) differs from the analysis of Moaz et al (2006) rather than in answering your criticism of my spreasheet demo. I think it is really important to for me to understand how these analyses differ if we really want to resolve this conflict. If I could see exactly what Moaz et al got right that Shaffer and I got wrong then I am pretty sure we could have this debate wrapped up with mututal agreement in no time.

You, as anyone else, should not feel insulted if others try to show your errors and help you to learn from them. But understandably this kind of interaction can lead to conflicts like it often does for example in school and home education. I have not asked you to answer the criticism of your spreadsheet demo. Instead I have tried to use those spreadsheets to show the problems in you argument.

But let’s now go the first problem. Until now I have claimed that you make a mistake which Maoz et al did not make. At the moment I am no more so sure about the innocence of Maoz et al. Their derivation of the equation (4) [v(t) = α(t)^1/3 * κ(t)^−1/3] (read: at the time t, velocity is alpha to the power of 1/3 times curvature to the power of -1/3) has certainly seemed to them very meaningful at that time and that may be their mistake, I think now. It also seems that they agree with me because in a later work Maoz et al 2013 they refer to that article very modestly only with this: “More recently, it was hypothesized that the power law may stem in part from correlated noise in the motor system (Maoz et al. 2006)”. So they made the same mathematical “invention” but saw later that it does not lead to anywhere. The problem is that we can derive (or devise) an infinite amount of valid mathematical equations but it is totally a different question to what tasks they can be applied.

Maoz et al (2006) did apply that equation by deriving further an equation (6) [β = −1/3 + ξ/3] where beta β is the linear regression coefficient of log(v) versus log(κ) and ξ (xi) is the linear regression coefficient of log(α) versus log(κ). From this they saw that: “Hence, if log(α) and log(κ) are statistically uncorrelated, the linear regression coefficient between them, which we termed ξ, would be 0, and thus from (6) the linear regression coefficient of log(v) versus log(κ), which we named β, would be exactly −1/3. Therefore, any trajectory that produces log(α) and log(κ) that are statistically uncorrelated would precisely conform to the power law in (1)” which they earlier termed as “the two-thirds power law”. In a footnote they say: “α being constant is naturally a special case of uncorrelated log(α) and log(κ).”

Now, what is wrong in above mathematical reasoning of Maoz et al? First, why the (4) is generally valid? Because it is equivalent with

(4a) α(t) = v(t)^3 * κ(t)

from which we see that whatever values the velocity and curvature will get in any moment of any trajectory and absolutely independently of the possible relationship between these values, we can always create from them (the values of velocity and curvature) the respective value of alpha. So alpha has no independent significance what so ever because its value depends on the values of velocity and curvature. Alpha depends on velocity and curvature but velocity and curvature do no way depend on alpha. This conclusion doesn’t depend at all on the way how (4) was initially derived or invented.

What about (6) and inferences from it? The core here is the question when does a trajectory produce log(α) and log(κ) that are statistically uncorrelated (which is the same that when does a trajectory obey the power law)? Of course log(α) and log(κ) are statistically uncorrelated when there is no dependence relationship between alpha and curvature. Above we saw that the value of alpha depends mathematically from both the curvature and the third power of velocity. A product of a multiplication has always a positive correlation to the multiplicands. Maoz et al said that constant alpha is a special case of uncorrelated alpha and curvature. That is in a way true (and in way possibly wrong) because the only possible cases of uncorrelated alpha and curvature are that either alpha or curvature is constant. In every other case there is a dependence relationship. But if curvature is constant and velocity varies they are uncorrelated and there is no power relationship between them. So the constant alpha is the only case when the trajectory obeys the power law. That is just the nowadays well know fact that constant affine velocity means full obedience of power law. But that fact does no way explain why sometimes (and often) the affine velocity is stable and sometimes not. This is the original research question of that so called power law research and it is no way (or at least not very significantly) touched by the above mathematical reasonings. (And this is, I think, what Maoz et al finally saw but M&S did not.)

Now we can go to the problem the “OVB analysis”. Omitted variable bias analysis is an important method when we are interested not only about the empirical (statistical) dependence between some variables in a data but also about the causal relationships in the area of the reality which we are studying. Here is a very important, interesting and illuminating example of possible application of OVB analysis. In many societies we can find a positive dependence between education and salary. If a person has got more / higher education then she probably has also higher salaries. From this correlation we could infer that the level of salary depends causally on the level of education. If that were the case then anyone and everybody could rise their salaries just by investing to more education. But reality is not that simple and that assumption is biased. The mistake (or rather one mistake) is that we do not notice that both education and salary level can depend (causally) on some third (and probably fourth and fifth and so on) variable. One famous this kind of (here) omitted variable is the genetically different abilities of people. If you have suitable good genes you can easily learn in schools and get high degrees and possibly you can also more easily proceed in your career and get higher salaries. Perhaps this is enough for us to understand that we should also search for other possibly better explaining variable and not omit them from our theories and hypotheses. (I must add that the socioeconomic level of parents is at least as important omitted variable.)

In an area of the power law research this means that velocity and curvature are certainly not the only variables that should be studied. It is quite sure and clear for everyone, I think, that the phenomenon could be never explained just by the causal relationship between velocity and curvature. (And much less by the mathematical relationship between them.) There must be other variables which affect the relationship and there can be many of them – and they can be different in different cases. Clearly the researchers are searching for them but I cannot and don’t want to say are they currently searching in the right dimension. But the “OVB analysis” suggested by M&S is not at all parallel with the real OVB analysis described above. They suggest to use the alpha (named D in their article) as an omitted variable. As I said above, alpha is not any external independent factor which could ever somehow affect and explain the relationship between velocity and curvature. Alpha is a multiplication product of the curvature and the (third power of) velocity. When it is added as an extra predictor to the regression analysis between curvature and velocity (or rather the logarithms of all variables to reveal the non-linear power relationship), the result is that there is always that power relationship, which is clearly an absolutely wrong result in many cases and tells nothing about the real empirical dependence between the velocity and curvature in the current data. This was very clearly demonstrated by the spreadsheet demo where that method produces an absolute (fake) power dependency between two random variables which are fully uncorrelated.

I hope you (everyone) can understand what I have written above. If there are problems, please ask. If there are smaller or bigger errors, please show them.

Best
Eetu

80

I know. And you have the same problem in your responding to my criticism. That’s because we, like all living things, are controllers, in fact, not just in theory.

That looks more like an obfuscation than a clarification. Affine velocity is not an “extra” predictor. It is one of the variables in the mathematical relationship between the measures of curvature and velocity that are used in determining whether or not there is a -1/3 power relationship between these measures.

My argument is that the measurement method – calculating velocity and curvature from the same movement trajectory-- and the analysis method – simple linear regression – have '“created” the power law phenonenon.

OK, let’s look at them one at a time.

OK, so you agree now that my equation:

log(V) = -1/3 * log (C) + 1/3 * log(A) … (1)

where V = velocity, C = Curvature and A = affine velocity

is, indeed, exactly the same as the one derived by Moaz et al. But now you think that there is something wrong with it because Maoz and Flash apparently no longer like it. Your evidence for this is that they don’t cite it in a more recent paper (thanks for the reference, by the way). But I looked at that paper and equation (1) is not used becuase it is not relevant to what they were studying.

Moab and Flash are not deriving a power law relationship from movement using regression analysis; they were doing a percepetual experiment (using the method of adjustment) to determine the power coefficients of various movements of a dot displayed on a computer screen, to determine which were movements perceived as having constant velocity. Good PCT-type experiment, by the way.

I don’t understand what this means. Could you give me an example of some small subset of equations from that " infinite amount of valid equations".

That’s what I’d like to know!!

That is not the reason it is valid! Equation (4) in Moaz et al is:
image

It is “valid” because it is derived from the computational formulas for velocity and curvature. This is the computational formula for velocity:

image

and this is the computational formula for curvature:

image

where the computaitonal formula for velocity has been substituted into equation (3) in the expression on the far right. Then by some simple algebra you get an expression for velocity as a function of curvarure and affine velocity (equation (4)).

The fact that this is not a valid argument can be seen if rearrange the equation so that curvature is the criterion (dependent) variable with velocity and affine velocity as the predictors and restate your conclusion as " we see that whatever values the velocity and alpha will get in any moment of any trajectory and absolutely independently of the possible relationship between these values, we can always create from them (the values of velocity and alpha) the respective value of curvature.

So you have clearly not shown that there is anything wrong with Moaz et al’s equation (4) (and M&S equivalent equation).

No, that is not the core question at all. The core question is “Does equation 6 correctly (and exactly) predict the value of the power coefficient of curvature (Beta) when affine velocity is omitted as a predictor variable”? And the answer, which is easily demonstrated computationally, is that it does.

I think i’ll stop here. Based on what you’ve already said it is clear to me (but not to you) that you do not understand regression or OVB analysis, (or to be nicer about it, you don’t understand these analyses the way I do). So we’re really not going to get anywhere with this.