This is going to be a little rant about diagrams, for nitpicky people. Diagrams are important for representing systems and understanding how they behave. A good diagram follows consistent rules, has a direct correspondence to equations or code associated with it. Diagrams in PCT are supposed to be more like engineering block diagrams, or analog computer setups, and not just lumps of boxes and arrows. Bad diagrams can generate confusion and misunderstanding.
So, here is one inconsistent diagram, not following its own rules set in the description under the figure.
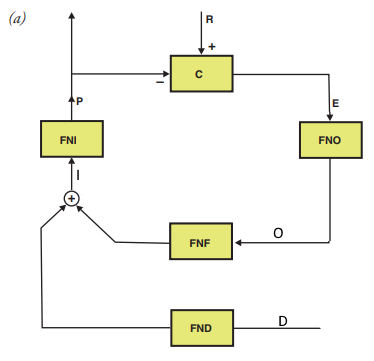
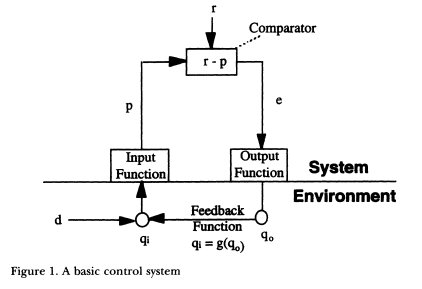
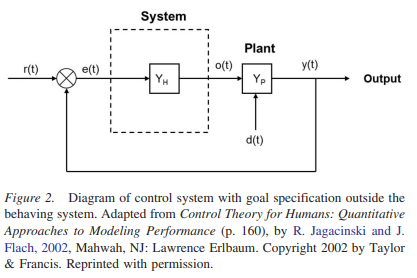
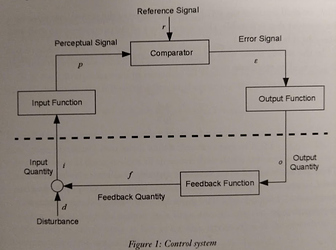
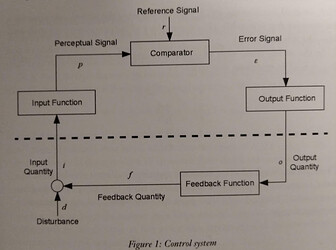
This is from one of Bill’s introduction to PCT texts. He says in the description: Loop functions are shown in gray. Variable names are inside circles, and a text box describes what they represent.
The problem here are two extra functions NOT shown in gray. One in the Disturbance function that takes in D and outputs Kd * D, and more importantly, the adding function taking in Kr * Qo and Kd * D, which is simply written under the feedback function.
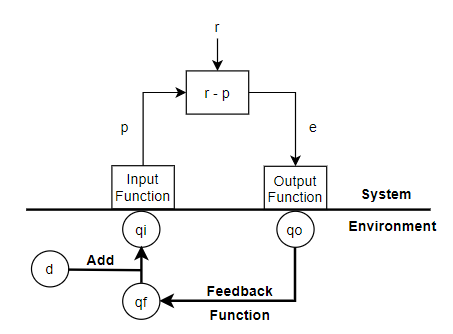
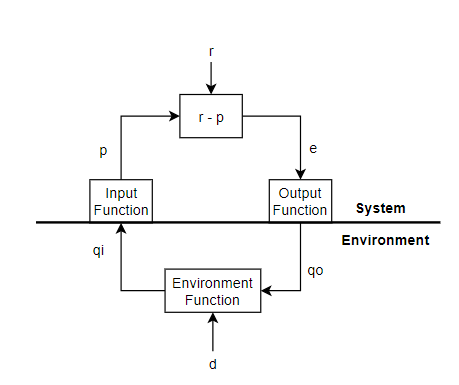
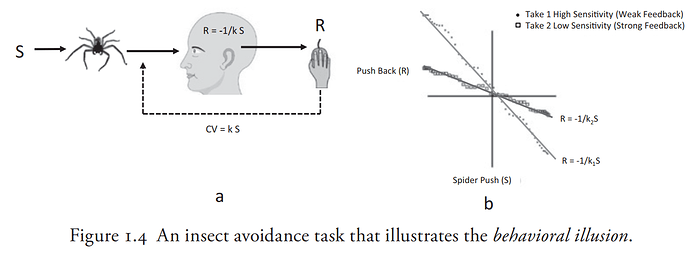
All good in the upper part. The environment should look something like this:
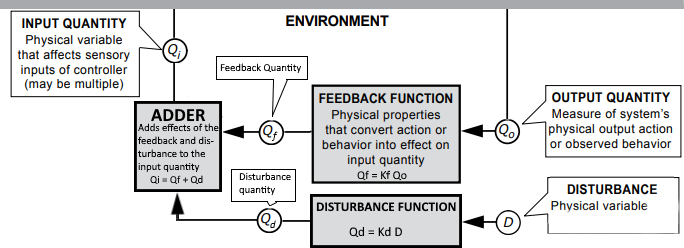
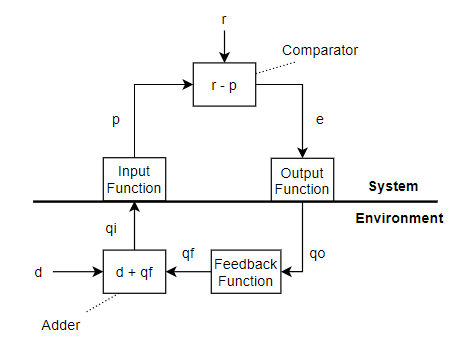
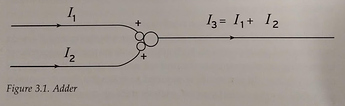
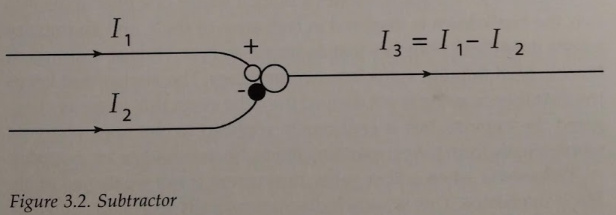
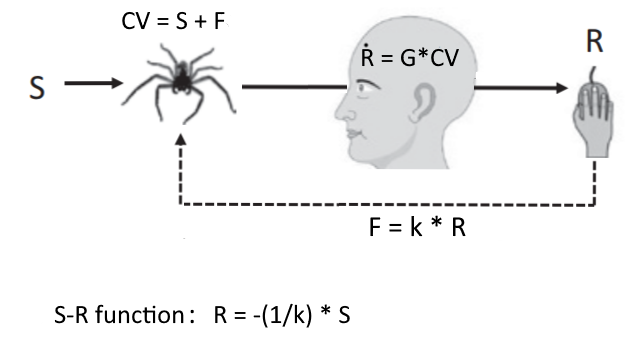
The comparator inside the system has its own box, why not the adder too? It is clearly an adder in the formula.
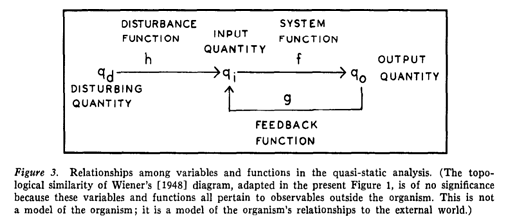
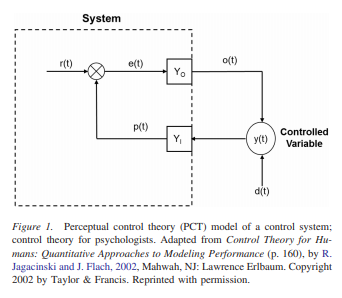
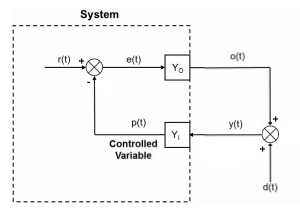
This is a good diagram, from LCS III, live demo:
I think something in the graphics is hidden, there should be a circle where the feedback quantity and disturbance meet. Every variable has a name, a line with an arrow, and numerical value. Every function has parameters and a box. Well, except for the ADDER, but at least there is an empty space for it (or a circle), and there is no disturbance function like above.
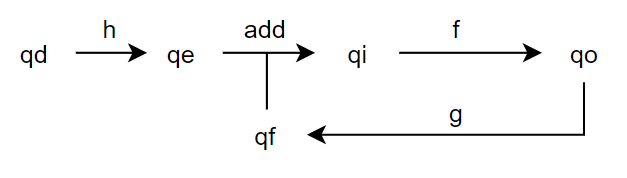
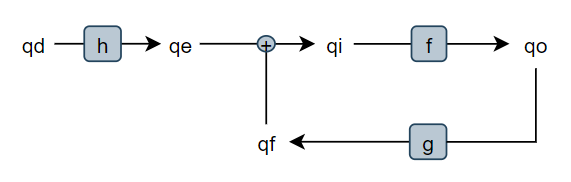
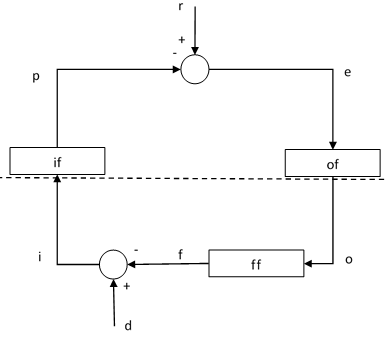
Here is an old diagram from DEMO2, Bill’s PCT tutorial. I think it is not consistent. Inside the system boundary, there are three functions, named above the diagram as Perception, Comparison and Action. Lines are variables, functions are in boxes.
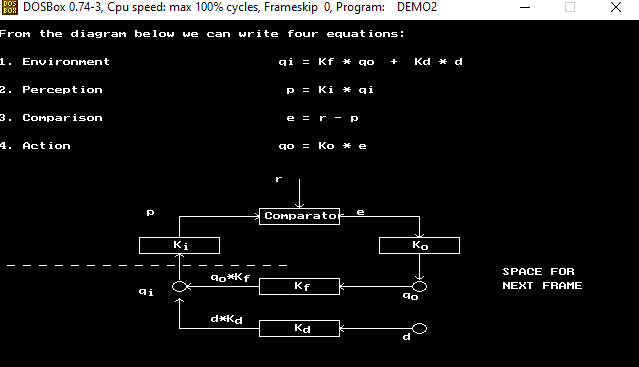
In the environment, quantities are in circles, the feedback function and the disturbance function are in boxes, and lines are what exactly? It is not clear at all. Functions are represented with boxes both inside and outside - there should not be any difference between representation of variables in the system and outside.
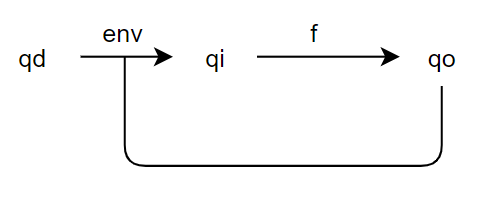
Here is how I made that diagram in the reproduction of DEMO2 a few years ago:
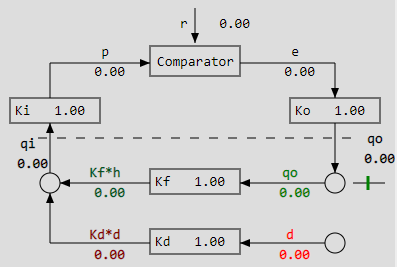
The only difference is where the qo, qi and d are placed, I think that makes it clear that lines are variables. Looking at it now, I would loose the circles for qo and d, and maybe replace the comparator with a circle too, because they have no clear purpose in the diagram. the d circle could possibly by a generator of smoothed random signals.
Another one of mine, from a few years ago:
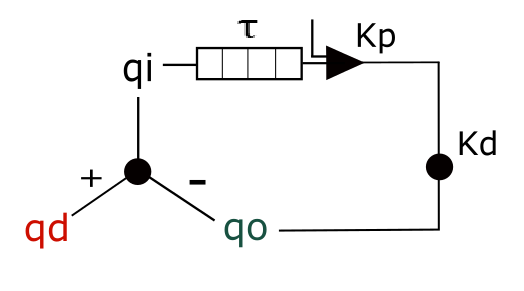
The t (tau) is representing a delay element, ok. The triangle has a parameter Kp and a reference signal, but the reference signal is not marked, so not good. It is supposed to be a comparator and an amplifier: x(t) = Kp * [ r - p[t-tau] ], and then the Kd is supposed to be a leak parameter for a leaky integrator, qo[t] = qo[t-1] - (x[t] - Kd * qo[t-1])*dt. There is an adder in the environment as a black circle, adding qd and qo; well, subtracting them, so it is another comparator, but has a different symbol than the comparator-amplifier triangle. Not sure why the variable names are ‘floating’ above lines. Also the leaky integrator symbol is the same as the adder/comparator on the left. Not very good.
Today, I’d probably make something more like one of these two:
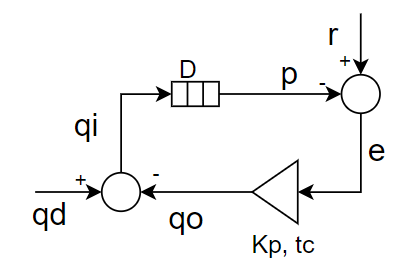
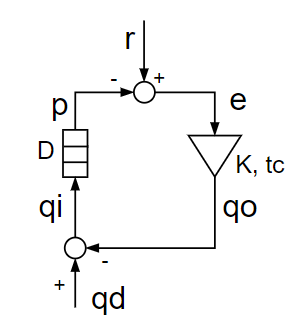
Could have some improvement in the delay element, it could also be a generic input function box, but this one has all the variables and function parameters.
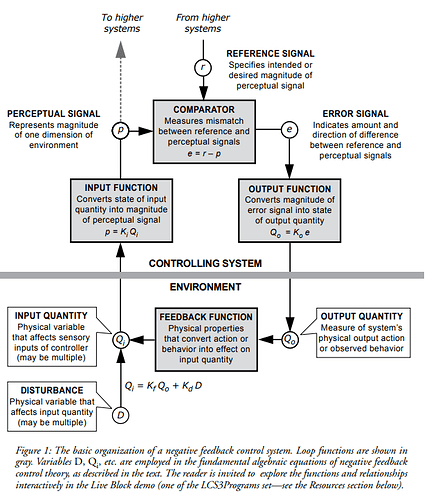
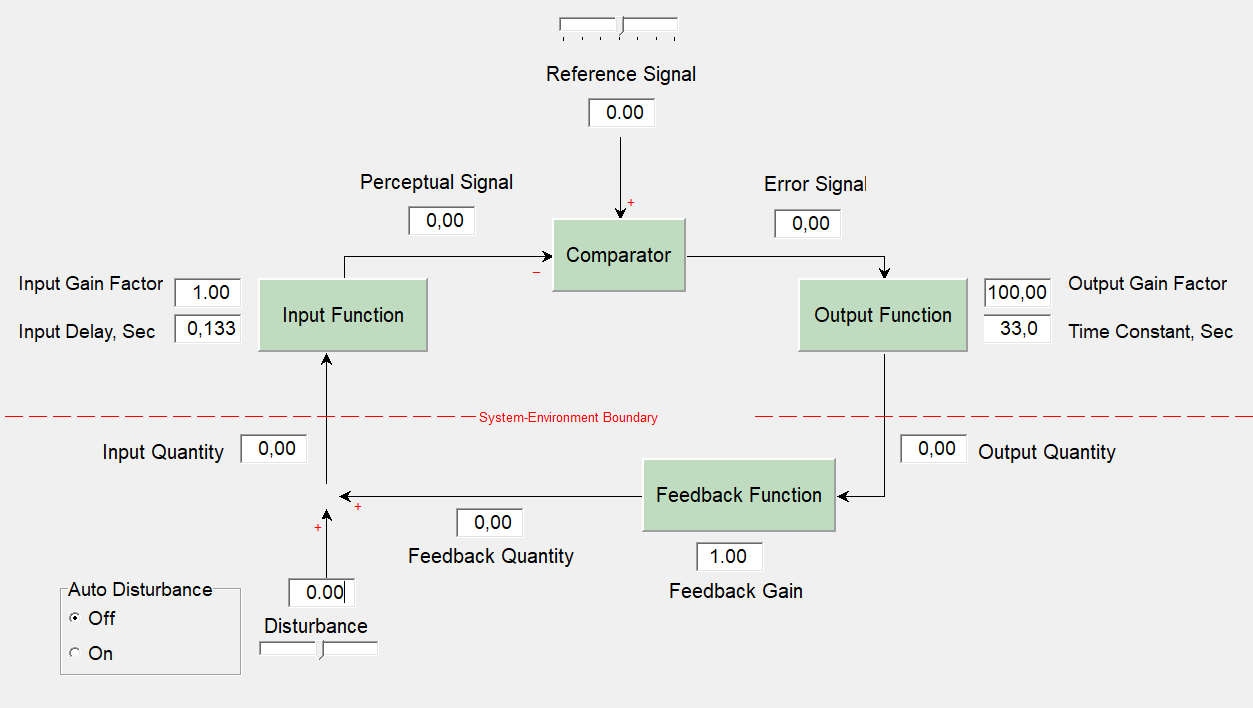
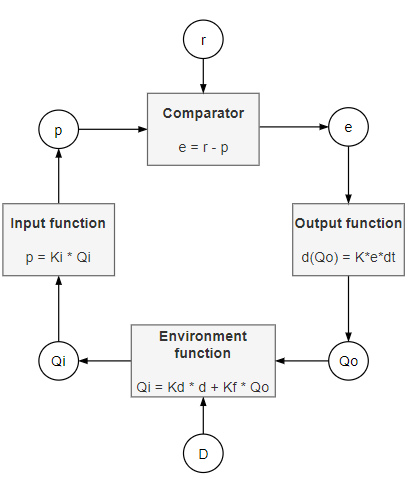
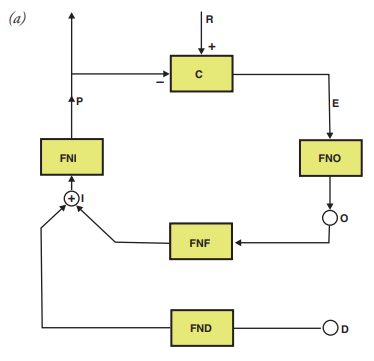 Fix:
Fix: